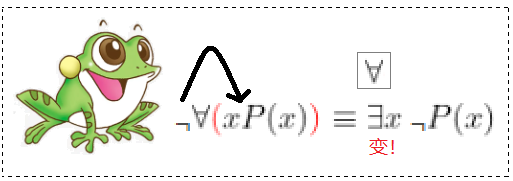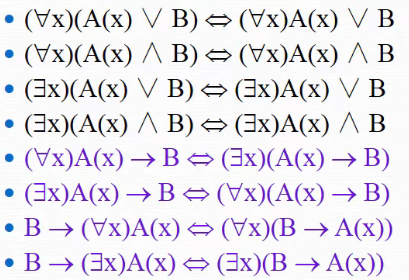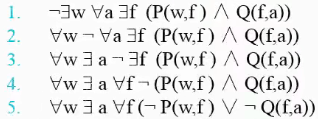【快乐离散数学】谓词与量词

您所在的位置：网站首页 › 联结词的性质 › 【快乐离散数学】谓词与量词

【快乐离散数学】谓词与量词

2024-07-04 18:55| 来源: 网络整理| 查看: 265

WEEK1：Propositional Logic, Propositional Equivalences, Predicates and Quantifiers, Nested Quantifiers.

写在前面：本系列博客为复习离散的学习笔记，内容主要参考自 Kenneth Rosen 的《Discrete Mathematics and Its Applications》和重庆大学刘然老师的《离散数学及其应用》课程。

🔗 视频教程：【重庆大学】《离散数学及其应用》刘然_哔哩哔哩_bilibili

Ⅰ. 谓词（Predicates）

0x00 引入：孙笑川，你坏事做尽！

0x01 谓词逻辑（Predicate logic）

0x02 命题函数（Propositional Function）

0x03 复合表达式

Ⅱ. 量词（Quantifiers）

0x00 引入：量化

0x01 全称量词（Full name quantifier）

0x02 存在量词（Existential quantifier）

0x03 惟一性量词

0x04 有限论域和无限论域

0x05 量词的性质

0x06 量词的优先级

0x07 变元的约束

Ⅲ. 谓词与量词（Predicates and Quantifiers）

0x00 谓词逻辑等价式

0x01 把量词看作析取或合取联结词

0x02 量化表达式的否定

0x03 狄摩根定律（De Morgan's laws）

0x04 命题公式的推广

0x05 量词辖域的扩张与收缩

0x06 量词分配等价式

0x07 语句到逻辑表达式的翻译

Ⅳ. 嵌套量词（Nested Quantifiers）

0x00 嵌套量词的概念

0x01 量词的顺序

0x02 嵌套量词到汉语的翻译

0x03 数学语句到嵌套量词的翻译

0x04 汉语语句到逻辑表达式的翻译

0x05 嵌套量词的否定

Ⅰ. 谓词（Predicates） 0x00 引入：孙笑川，你坏事做尽！

假设我们知道："人皆有一死 "，"孙笑川是个人"。

❓ 思考：这是否意味着 "孙笑川终有一死" ？

"哈哈哈哈啊哈哈，开幕雷击"

💡 解读：不能用命题逻辑来表示，需要一种语言来谈论对象、它们的属性和它们的关系。

假设 $p$ 表示 "人皆有一死"， $q$ 表示 "孙笑川是个人"，设要死为 $r$ ：

$(p\wedge q)\rightarrow r$

这个式子很可惜不是一个永真式，当整个命题取 $T,F$ 时这个句子就可能取 $F$ 。

而我们知道这个确实是真的，人总有一死，那么问题出来哪里？

问题出来我们的描述能力还不够强，句子之间有内在联系。

即 "人皆有一死" 和 "孙笑川是个人" 之间有内在联系， $r$ 也是有内在联系的。

因此这个地方我们就不能用这种命题逻辑去表达，应该用更为精细的数学符号体系去表达。

因为命题逻辑并不足够，所以要学习谓词逻辑，本节我们将演示用谓词逻辑来进行命题的推论！

0x01 谓词逻辑（Predicate logic）

能够表示客体的性质和关系的，我们称之为谓词。谓词逻辑有以下特征：

变量（variable）： $x,y,z$ 谓词（predicate）： $P(x),\, M(x)$ 量词（classifier）： $\forall ,\exists$

像这里的 $P(x)$ 就像一个函数的形式，我们叫它命题函数（Propositional Function）。

命题函数就是命题的概括：

它们包含变量和谓词，例如 $P(x)$ . 变量可以用来自其论域（Domain）的元素赋值

这里的 "论域" 可以理解为高中学的定义域，以 "变量来自于哪里" ，

所以我们在明确命题函数时我们一般要谈论其论域才有意义。

0x02 命题函数（Propositional Function）

❓ 思考：命题函数是命题吗？显然不是，因为命题函数的变量是不确定的。

但是，当命题函数的变量被域中的值替换时，命题函数就能变成命题。

（并且这个命题具有真值，当然还可以由 "量词绑定" 变成命题，这个我们后面再说）

这时候我们就称 $P(x)$ 是命题函数 $P$ 在 $x$ 处的值，把 $x$ 赋进来的时候它就变成了个命题，

谓词在 $x$ 处的值就得到了真假，有了真假就变成了命题。下面我举个例子：

💬 假设 $P(x)$ 表示 $x0$ ，定义域为整数。既然是整数，我们就可以取实数上所有整数来带入到 $P(x)$ 中判断真假：

$P(-3)$ 为假（比如我们把 -3 带入此时我们就可以判断真假了） $P(0)$ 为假（ 0 > 0 显然是假） $P(3)$ 为真（带入 3 后，3>0 又是真了）

当这个命题函数可真可假，它不是命题，但是当用具体的变元（或变量被赋值时），它就变成了一个具体的、可判断真假的命题了。

我们通常定义域用 $U$ 来表示，所以在上例中 $U$ 是整数。

上面的命题函数只有一个元 $x$ ，所以我们称之为一元谓词，命题函数也可以有多个元。

比如下面的命题函数就有 $x,y,z$ 三个元，我们称之为三元谓词：

…… n元谓词，n-ary predicate

💬 设 $x+y=z$ 用 $R(x,y,z)$ 表示， $U$ （对于所有三个变量）为整数，找出下列真值：

$R(2,-1,5)$ （再次强调，此时的命题函数已经变为命题了） ${\color{DarkGreen} F}$ $R(3,4,7)$ ${\color{DarkGreen} T}$ $R(x,3,z)$ ${\color{DarkGreen} R(x,z) , x+y=z}$ 无法判断真假

🔑 解析：2+(-1)=5 吗？No，所以选F；3+4=7，Yes，所以选T；x+3=z 还是有两个变元，我们无法判断真假，这样的一个式子不是命题（这里只有 x 和 z 都有具体的数时才能变成一个命题）。它就相当于 $R(x,z)$ ，等于 $x+3=z$ 这样的一个式子。

因为命题没有变量我们也称之为零元谓词。通过上面这个例子我们不难发现，每确定一个变量就会少一个元，如果把所有的变量都用值代替的话，那就变成了零元谓词（即命题）。

相你信读到这里已经掌握了其中的奥妙，我们来练一题：

💬 现在让 $x-y=z$ 用 $Q(x,y,z)$ 表示， $U$ 为整数，找出下列真值：

$Q(2,-1,3)$ ${\color{DarkGreen} T}$ $Q(3,4,7)$ ${\color{DarkGreen} F}$ $Q(x,3,z)$ ${\color{DarkGreen} x-3=z}$ 无法判断真假

0x03 复合表达式

我们可以通过命题逻辑的联结词 $\wedge ,\vee ,\rightarrow ,\leftrightarrow$ 来构成复合命题，

同样地，我们也可以用 $\wedge ,\vee ,\rightarrow ,\leftrightarrow$ 连接谓词来构成更复杂的为此公式，来表达更复杂的语句。

💬 如果 $P(x)$ 表示 $x0$ ，找到这些真值：

$P(3) \vee P(-1)$ ${\color{DarkGreen} T}$ $P(3) \wedge P(-1)$ ${\color{DarkGreen} F}$ $P(3)\rightarrow P(-1)$ $P(3) \leftrightarrow P(-1)$

不难看出，如果我们把值带进去再加上联结词我们就可以像命题公式一样得到它们的真值。

但是有些变量没有带入具体的值，我们知道，带有变量的表达式不是命题，因此没有真值：

$P(3)\wedge P(y)$ # y 有可能是 T 有可能是 F，这取决于论域，在这种情况下无法判断真假 $P(x)\rightarrow P(y)$

当与量词一起使用时（我们下面会介绍量词），这些表达式（命题函数）就变成了命题。

因此，当和两次一起使用的时候，他反而就变成了命题。

Ⅱ. 量词（Quantifiers） 0x00 引入：量化

我们需要量词来表达自然语言中的意思，包括所有和某些：

人皆有一死有些猫没有毛

最重要的两个量词：

全称量词（Full name quantifier）：符号为 $\forall$ 存在量词（Existential quantifier）：符号为 $\exists$

我们写成 $\forall xP(x)$ 和 $\exists xP(x)$ ：

$\forall xP(x)$ 表示 $P(x)$ 对 $x$ 在其论域的所有值为真。 $\exists xP(x)$ 表示 $P(x)$ 论域中存在一个個體满足 $P(x)$ 。

量词在这些表达式中必须绑定变量 $x$ ，可以理解为 $x$ 对它进行了一个限制。

0x01 全称量词（Full name quantifier）

$\forall xP(x)$ 可读作 " 对所有 $x,P(x)$ " 或 " 对任意 $x,P(x)$ "

若 $P(x)$ 表示 " $x0$ " 且 $U$ 是整数，则 $\forall xP(x)$ 是假。若 $P(x)$ 表示 " $x0$ " 且 $U$ 是正整数，则 $\forall xP(x)$ 是真。若 $P(x)$ 表示 " $x$ 是偶数 " 且 $U$ 是整数，则 $\forall xP(x)$ 是假。

🔑 解析：

对于任意的整数都大于 0 显然是错的，比如 -1，任意 $x$ 只要有一个不满足就可以判断为假。本来 $P(x)$ 是带有变元的，但这里有一个量词在做一个限定，反而使其能够判断真假了。 $U$ 是正整数，在正整数的情况下对任意的 $P(x)$ 同样也能够得到真假，对于任意正整数带入 $x0$ 都是真，所以 $\forall xP(x)$ 是真的。 $U$ 是正整数，谓词是 " $x$ 是偶数 "，正整数里面肯定有奇数，所以对于任意来说 $\forall xP(x)$ 必然为假。所以这种情况我们也能判断真假，因此成为了一个命题。

🔺 总结：所以 "只要看到 $x$ 它就不是命题" 这种说法是错的，当带有量词去做限定时，它已经被 "量化" 了，它就自然成为一个命题了，即零元名词（即使里面带有变元）。

0x02 存在量词（Existential quantifier）

$\exists xP(x)$ 可读作 "对某个 $x,P(x)$ " 、"至少有一个 $x$ 满足 $P(x)$ " 或 "存在 $x,P(x)$ " 。

核心就是 —— 只要找到一个满足的条件，这个表达式就为真。

若 $P(x)$ 表示 " $x0$ " 且 $U$ 是整数，则 $\exists xP(x)$ 为真；若 $U$ 是正整数， $\exists xP(x)$ 也是真。

若 $P(x)$ 表示 " $x0$ " 且 $U$ 是正整数，则 $\exists xP(x)$ 为假。（一个能满足的条件都没有）

如果 $P(x)$ 表示 " $x$ 是偶数 "，且 $U$ 是整数，则 $\exists xP(x)$ 是真。

由此可见，存在量词和论域有着很大的关系，在取不同的论域时，它可真可假。

0x03 惟一性量词（Uniqueness quantifier）

$\exists \, !\, xP(x)$ 表示存在惟一的一个 $x$ 能使 $P(x)$ 为真。我们通常用以下语言表达：

"恰好存在一个 $x$ ，能使 $P(x)$ 为真。""有且只有一个 $x$ ，能使 $P(x)$ 为真。" 若 $P(x)$ 表示 " $x+1=0$ " 且 $U$ 是整数，则 $\exists \, !\, xP(x)$ 为真。

（这里 $x$ 只能是 $-1$ , 并且 $x$ 存在于 $U$ ，所以满足惟一性）

但是如果 $P(x)$ 表示 " $x0$ "，则 $\exists \, !\, xP(x)$ 为假。

（有无穷多的多 $x$ 都是大于 0 的，显然不满足唯一性）

惟一性量词虽然是存在量词的一种，但并不是必要的。因为存在一个惟一的 $x$ 使得 $P(x)$ 为真可以表示为：

$\exists x\, (\, P(y) \wedge \forall y(P(y)\rightarrow y=x)\, )$

0x04 有限论域和无限论域

💭 对量词的思考：当论域是有限的，我们可以认为量化是对论域中所有元素的循环。

比如对于任意的 $xP(x)$ 你是如何去考虑它真假的呢？

评估 $\forall xP(x)$ 通过在论域中所有 $x$ 循环（因为有限，所以我们可以在这里面挨个试）：

若每一步 $P(x)$ 都是真，则 $\forall xP(x)$ 是真。如果有一步 $P(x)$ 是假，则 $\forall xP(x)$ 是假，则不满足 "任意 $x$ 都满足" 的性质，且结束循环。

比如 "全班同学今天都来上课了" ，点名大家都到了，那就为真。

如果点名的时候哪怕只有一个人没到，比如孙笑川（所以坏事都是孙狗做的），那就为假。

评估 $\exists xP(x)$ 通过在论域中所有 $x$ 循环：

如果某步使 $P(x)$ 为真，哪怕只有一步，则 $\exists xP(x)$ 就是真，且结束循环。如果循环结束都没有找到一个能使 $P(x)$ 为真的，则 $\exists xP(x)$ 为假，一个都没有。

比如 "期末考试我们班有满分"，只要有一个人是满分，这句话就能成为真。

但是如果一个满分都没有那这句话铁定是假的了，"期末考试我们班有满分" 就是胡说八道。

即使论域是无限的，我们仍然可以这样考虑量词，但是循环在某些情况下将不会终止。

一般情况下我们不需要去论证那么多，比如 $x 0$ ，虽然无限但是我看一眼正负就能判断。

0x05 量词的性质

📚 性质： $\forall xP(x)$ 和 $\exists xP(x)$ 的真值依赖于命题函数 $P(x)$ 和论域 $U$ 。

如果 $U$ 是正整数，且 $P(x)$ 表示语句 " $x2$ " ，则 $\exists xP(x)$ 是真，但是对于 $\forall xP(x)$ 是假。如果 $U$ 是负整数，且 $P(x)$ 表示语句 " $x2$ " ，则 $\exists xP(x)$ 和 $\forall xP(x)$ 均是真。如果 $U$ 由 $3,4,5$ 组成的集合，且 $P(x)$ 表示语句 " $x2$ "，则 $\exists xP(x)$ 和 $\forall xP(x)$ 均是真。但是如果 $P(x)$ 表示语句 " $x2$ " ，则 $\exists xP(x)$ 和 $\forall xP(x)$ 均是假。

由此看来，它是依赖论域的。

0x06 量词的优先级

量词 $\forall$ 和 $\exists$ 比所有逻辑运算符的优先级都要高。

例如， $\forall xP(x)\vee Q(x)$ 意思是 $(\, \forall xP(x)\, )\vee Q(x)$ 。对于任意 $xP(x)$ 析取 $Q(x)$ 。

它和 $\forall x(\, P(x)\vee Q(x)\: )$ 意思有所不同 —— 对于任意 $x$ ， $P(x)$ 析取 $Q(x)$ 。

这是 $\forall x$ 后面管了所有表达式，此时 $\forall x$ 作用的范围就是 $P(x)\vee Q(x)$ 。

📌 注意：可是人们经常喜欢用 $\forall xP(x)\vee Q(x)$ 表示 $\forall x(\, P(x)\vee Q(x)\: )$ ，这是错误的！

0x07 变元的约束

📚 定义：在谓词公式中，形如 $(\forall x)P(x)$ 和 $(\exists x)P(x)$ 的部分，称为谓词公式的 $x$ 约束部分。

$(\forall x)P(x)$ 和 $(\exists x)P(x)$ 中的 $x$ 叫做量词的指导变元或作用变元（可以理解为指导员）

$P(x)$ 称为相应量词的作用域或辖域。（可以理解为管辖范围）

在 $\forall x$ 和 $\exists x$ 的辖域中， $x$ 的所有出现都统称为约束出现，相应的 $x$ 称为约束变元。（可以理解为被管对象）

最后， $P(x)$ 中除约束变元，意外出现的变元成为是自由变元。（可以理解为闲散人员）

老师就好比是指导变元，管理你们班，老师的管辖范围就是你们班所有同学，你作为被管的，就是约束变元。而自由变元就好比有个同学到去你们班旁听，他在你们班上就是自由的，他想来上课就来、作业想交就交，不交老师也管不了他，虽然形式上似乎能管，因为他人可以在这个班上，但实际上他不是你们班的人，老师是管不了他的，因为他是旁听的。

$\forall x(H(x,y))$ ， $x$ 就是班上同学， $y$ 是旁听生， $\forall x$ 即老师能管班上同学 $x$ 。

💭 例如：

$\forall x{\color{Blue} (}H(x,y)\rightarrow \exists y{\color{Red} (}W(y)\wedge L(x,y,z){\color{Red} )}{\color{Blue} )}$

$\forall x{\color{Blue} (}H(x)\rightarrow W(y){\color{Blue} )}\rightarrow \exists y{\color{Red} (}F(x)\wedge L(x,y,z){\color{Red} )}$

一个公式的约束变元所使用的名称符号是无关紧要的，如 $(\forall x)M(x)$ 与 $(\forall y)M(y)$ 意义相同。

Ⅲ. 谓词与量词（Predicates and Quantifiers） 0x00 谓词逻辑等价式

当且仅当由谓词和量词构成的语句具有相同的真值时，他们在逻辑上是等价的。

因为它有可能是无限的，所以我们就要求：

对于每一个被带入的这些语句的谓词。对每个论域中所使用的变量表达式。

表示仍然使用三条杠，即符号 $S\equiv T$ 表示 $S$ 和 $T$ 在逻辑上是等价的。比如：

$\forall x$ ¬¬ $S(x)\equiv \forall x\, S(x)$

双重否定即肯定：¬¬ $p$ 满足逻辑非，就是等于原命题。所以这两个式子是等价的。

0x01 把量词看作析取或合取联结词

如果论域是有限的，一个全称量化的命题等价于每个量词的合取，一个存在量化的命题等价于每个量词命题的析取。

如果 $U$ 由整数 $1,2,3$ 组成：

$\forall xP(x)\equiv P(1)\wedge P(2)\wedge P(3)$ $\exists xP(x)\equiv P(1)\vee P(2) \vee P(3)$

即使域是无限的，我们仍然可以以这种方式考虑量词，但是没有量词的等价表达式将是无限长的。

0x02 量化表达式的否定

设 $\forall xJ(x)$ 表示 "班上每个学生都上过Java课程"， $J(x)$ 表示 " $x$ 上过Java课程 "，且域是班级的学生。

否定原来的陈述给出 "并不是班上的所有学生都上过Java课程"，这意味着 "你们班有一个学生没有上过Java课程"。

则 ¬ $(\forall xJ(x))$ 和 $\exists x$ ¬ $J(x)$ 是等价的。

设 $\exists xJ(x)$ 表示 "这个班有个学生上过Java课程"， $J(x)$ 表示 " $x$ 上过Java课程 "。

否定原来的说法就会得到 "这个班没有一个学生上过Java课程"。这意味着 "这个班的每个学生都没有上个Java课程"。

所以 ¬ $\exists xJ(x)$ 和 $\forall x$ ¬ $J(x)$ 是等价的。

0x03 狄摩根定律（De Morgan's laws）

否定量词的狄摩根定律是：

📚 由表中推理可知：

¬ $\forall {\color{Red} (}xP(x){\color{Red} )} \equiv \exists x$ ¬ $P(x)$

¬ $\exists{\color{Red} (}xP(x){\color{Red} )}\equiv \forall x$ ¬ $P(x)$

可以将 ¬ 想象成一只青蛙，而这就是个青蛙跳，每跳一级任意变存在，存在变任意。

0x04 命题公式的推广

在命题公式中成立的式子，用谓词公式去替代换其中相应的命题变元，得到的公式依然成立。比如：

$\forall x(P(x)\rightarrow Q(x))\Leftrightarrow \forall x($ ¬ $P(x)\vee Q(x))$

¬ $\forall xP(x) \vee$ ¬ $\forall xQ(x)\Leftrightarrow$ ¬ $(\forall xP(x) \wedge \forall xQ(x))$

0x05 量词辖域的扩张与收缩

量词辖域中如果有合取或析取项，且其中有一个是命题，

则可以将该命题移至量词辖域之外，如：

💭 举个例子：

$(\forall x)(A(x)\vee B)\Leftrightarrow (\forall x)A(x)\vee B$

名义上 $x$ 是管 B 的，但实际上是管不到的，所以可以将管不到的 B 移到括号外面，变成后面的式子。按刚才举的例子来说就是：

旁听生如果想站到教室外面（即收缩）上课，是可以的。

反过来，旁听生也可以进教室（即扩张），上课，也是可以的。

0x06 量词分配等价式

设 $A(x)$ 、 $B(x)$ 是任意的含自由出现个体变元的公式，则：

$\forall x(A(x)\wedge B(x)) \Leftrightarrow \forall xA(x)\wedge \forall xB(x)$ $\exists x(A(x)\vee B(x)) \Leftrightarrow \exists xA(x)\vee \exists xB(x)$

0x07 语句到逻辑表达式的翻译

💭 例一：把下面句子转换出谓词逻辑表达式："这个班上的学生都上过Java课程。"

解1：如果 $U$ 是班级中的所有学生，定义一个命题函数 $J(x)$ 表示 " $x$ 上过Java课程"，则翻译为 $\forall xJ(x)$ 。

解2：但是如果 $U$ 是所有人，也定义一个命题函数 $S(x)$ 表示 " $x$ 是班级中的一名学生"，则翻译为 $\forall x(S(x)\rightarrow J(x))$ 。

注意： $\forall x(S(x)\wedge J(x))$ 是不正确的，它的意思是 "是个学生都学过Java课程并且在我们班上"，这样显然不符合题意。

💭 例二：把下面的句子改成谓词逻辑："这个班的一些学生上过Java课程"。

解1：如果 $U$ 是班级中的所有学生，翻译成 $\exists xJ(x)$ 。

解2：但是如果 $U$ 是所有人，则翻译成 $\exists x(S(x)\wedge J(x))$ 。

注意： $\exists (S(x)\rightarrow J(x))$ 是不正确的，它的意思是 "只要是我们班的同学都学过 Java 课程"。

💭 例三：翻译 "这个班有学生去过蒙大拿" 、"这个班的每个学生都去过蒙大拿和理塘"。

解：

① 令 $M(x)$ 表示 " $x$ 去过蒙大拿"， $S(x)$ 表示 " $x$ 是班里的学生"， $U$ 表示的域：所有人。

${\color{Red} \exists x}(S(x){\color{Red} \wedge } M(x))$

② 增加 $L(x)$ 表示 " $x$ 去过理塘"。

${\color{Red} \forall x}(S(x){\color{Red} \rightarrow} (M(x)\vee C(x)))$

📌 注：

我们常常把表示客体某种性质的谓词称为特性谓词（例如上面的 $S(x)$ ）。存在量词对应的特性谓词做合取项，全称量词对应的特性谓词做条件联结词的前件。

🔺 总结：一元谓词表性质，多元谓词表关系。特性谓词做合取项时用特性谓词做合取项，全称量词时特性谓词做前件。

💬 我们现在可以解决本章开头引入部分提到的孙笑川的例子了。

设命题函数 $Sxc258(x)$ 表示 " $x$ 是一个人"， $Motal(x)$ 表示 " $x$ 皆有一死"，指定论域为所有人。

这两个前提是：

$\forall x(Sxc258(x) \rightarrow Mortal(x))$ $Man(Socrates)$

结论是： $Mortal(Socates)$

💭 我们来做一道口碑不错的练习题：

$U= \left \{{\color{Blue} fleegles,snurds,thingamabobs} \right \}$

$F(x)$ ：x is a fleegle $S(x)$ ：x is a snurd $T(x)$ ：x is a thingamabob

① 翻译："Everything is a fleegle."

解： $\forall xF(x)$

② 翻译： "Nothing is a snurd."

解： $\forall x($ ¬ $S(x))$ 或 ¬ $\exists (xS(x))$ （狄摩根青蛙跳，它们是等价的）

③ 翻译："All fleggles are snurds."

解： $\forall x(F(x)\rightarrow S(x))$

④ 翻译："Some fleegle are thingmabobs." （既是什么又是什么，两个都是，要翻译成合取）

解： $\exists x(F(x) \wedge T(x))$ （注意！不能翻译成条件。只要是存在量词，它是什么是特性谓词时就可以翻译成合取项）

⑤ 翻译： "No snurd is a thingamabob"

解： ¬ $\exists x(S(x)\wedge T(x))$ 或 $\forall x($ ¬ $S(x)\vee$ ¬ $T(x))$

⑥ 翻译： "If any fleegle is a snurd then it is also a thingamabob."

解： $\forall x((F(x)\wedge S(x))\rightarrow T(x))$

Ⅳ. 嵌套量词（Nested Quantifiers） 0x00 嵌套量词的概念

嵌套量词通常是表达句子意义以及计算机科学和数学中的重要概念中所必须的。

比如："每个实数都有一个逆"，可用其表达为：

$\exists\, x\exists y\, (x+y=0)$ ，其中 x 和 y 的定义域是实数。

想要表达这种数学概念，只用一个变元表示就不礼貌了，像这里用两个变元去表达就会很容易。

我们也可以考虑为嵌套命题函数：

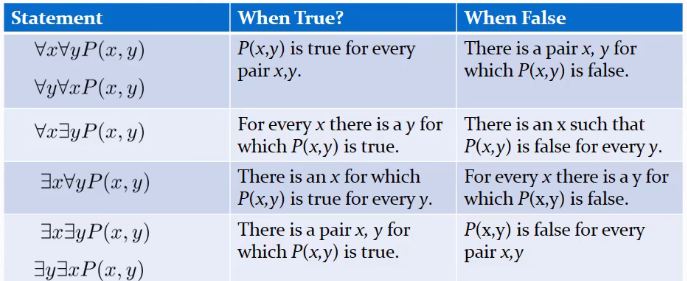
$\forall x\exists y(x+y=0)$ 可视为 $\forall xQ(x)$ 期中 $Q(x)$ 表示 $\exists yP(x,y)$ ， $P(x,y)$ 表示 $(x+y=0)$ 。

理解嵌套量词：

如果 $\forall x\forall yP(x,y)$ 为真，对 $x$ 所有制做循环：

每一步，对 $y$ 值做循环。如果对于某些 $x$ 和 $y$ ， $P(x,y)$ 为假，则 $\forall x\forall yP(x,y)$ 为假且外部和内部循环都终止。

$\forall x\forall yP(x,y)$ 为真，如果外循环在遍历每个 $x$ 后结束。

如果 $\forall x\exists yP(x,y)$ 为真，对 $x$ 所有值做循环：

每一步，对 $y$ 所有值做循环。当找到一对 $x$ 和 $y$ 使得 $P(x,y)$ 为真，内循环结束。如果没有找到 $y$ 使 $P(x,y)$ 为真，外循环终止因为 $\forall x\exists yP(x,y)$ 已经证明为假。

$\forall x\exists yP(x,y)$ 为真，如果外循环在遍历每个 $x$ 之后结束。

📌 注意：如果变量的域使无限的，那么这个过程实际上使不能执行的。

0x01 量词的顺序

可以随便换顺序：令 $P(x,y)$ 为语句 $x+y=y+x$ 。假设 $U$ 是实数，则 $\forall x\forall yP(x,y)$ 和 $\forall y\forall x(x,y)$ 有相同的真值。

不能随便换顺序：令 $Q(x,y)$ 为语句 $x+y=0$ 。假设 $U$ 是实数，则 $\forall x\exists yP(x,y)$ 为真，单 $\exists y\forall xP(x,y)$ 为假。

例一：令 $U$ 为实数，定义 $P(x,y):x\cdot y=0$ ，求下列真值：

$\forall x\forall yP(x,y)$ 解：对任意的 $x$ 和任意的 $y$ 乘起来都是0，这显然是 $F$ 。 $\forall x\exists yP(x,y)$ 解：对任意的 $x$ 和存在 $y$ 乘起来是0， $y$ 取0即可，为 $T$ 。 $\exists x\forall yP(x,y)$ 解：同上，这次是 $x$ 是存在 $y$ 是任意了，还是为 $T$ 。 $\exists x\exists yP(x,y)$ 解：存在 $x$ 和存在 $y$ 乘起来都是0，这当然太行了， $T$ 。

例二：令 $U$ 为实数，定义 $P(x,y):x/y=1$ ，求下列真值：

$\forall x\forall yP(x,y)$ 解：一眼 $F$ 。 $\forall x\exists yP(x,y)$ 解： $x$ 取0时， $0/y$ 无论 $y$ 怎么变结果都必然是 0， $F$ 。 $\exists x\forall yP(x,y)$ 解： $x$ 除任意的 $y$ 都要等于1， $F$ 。 $\exists x\exists yP(x,y)$ 解： $T$ 。

两个变量的量化：

0x02 嵌套量词到汉语的翻译

💭 翻译下列语句：

$\forall x(C(x)\vee \exists y(C(y)\wedge F(x,y)))$

其中 $C(x)$ 表示 " $x$ 有一个计算机"， $F(x,y)$ 表示 " $x$ 和 $y$ 是好朋友"， $x$ 和 $y$ 的定义域包含了学校的所有学生。

解：学校的每个学生 (都有一台电脑或有一个朋友有一台电脑) 。

$\exists x\forall y\forall z((F(x,y)\wedge F(x,z)\wedge (y\neq z))\rightarrow$ ¬ $F(y,z))$

解：有某个学生，他的所有朋友都不是彼此的朋友。

0x03 数学语句到嵌套量词的翻译

💭 将 "两个正整数的和总是正的"，转换出逻辑表达式。

解：

重写语句，使隐含的量词和域显式表达。"对于每两个整数，如果这些整数都是正的，那么这些整数的和就是正的"。引入变量 $x$ 和 $y$ ，并获得指定的定义域："对于所有正整数 $x$ 和 $y$ ， $x+y$ 为正。"

结果是： $\forall x\forall y((x0)\wedge (y0)\rightarrow (x+y0))$ ，这两个变量的域包含所有整数。

💭 用量词来表示语句 "世界上有一个女人乘过所有航线上的航班"。

解：

令 $P(w,f)$ 表示 " $w$ 搭乘过航班 $f$ "， $Q(f,a)$ 表示 " $f$ 是航线 $a$ 上的航班"。

$w$ 的域是所有女人， $f$ 的域是所有航班， $a$ 的域是所有航线。

则句子可以表示为： $\exists w\forall a\exists f(P(w,f)\wedge Q(f,a))$

0x04 汉语语句到逻辑表达式的翻译例一：兄弟是兄弟姐妹： $\forall x\forall y(B(x,y)\rightarrow S(x,y))$ 例二：每个人都喜欢别人： $\forall x\exists yL(x,y)$ 例三：有一个人是每个人都爱的： $\exists x\forall yL(x,y)$ 例四：有一个人爱着另一个人： $\exists w\exists fL(w,f)$ 例五：每个人都喜欢自己： $\forall wL(w,w)$

0x05 嵌套量词的否定

关于一个女人搭乘过所有航线上的航班的逻辑表达式：

$\exists w\forall a\exists f(P(w,f)\wedge Q(f,a))$

部分1：用量词来表达 "世界上没有哪位女人做过世界上每条航线的航班"。

解： ¬ ${\color{Red} (}$ $\exists w\forall a\exists f(P(w,f)\wedge Q(f,a))$ ${\color{Red} )}$