【线性代数本质】4：矩阵乘法本质

前面所讲的几节内容中涉及的变换都是单一的变换，那么如果你想描述多种连续的变换呢，或者称为复合变换

比如下图，先将平面逆时针旋转90°，然后再进行剪切。这很明显是两个变换，但是从总体上看可以看作是一个复合变换，是旋转和剪切作用的总和

和其他变换一样，描述这种变换我们也可以通过记录变换后的 i j ij ij来实现，矩阵表示为 ( 1 − 1 1 0 ) \begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix} (11​−10​)。这一新的矩阵捕捉到了两个变换的总体效应，但它的确是一个单独的作用

按照我们前文所讲，如果让一个向量 ( x y ) \begin{pmatrix} x\\ y\end{pmatrix} (xy​)乘以矩阵就会对其施加该矩阵所表示的线性变换，那么如果按照变换两次的角度来看，应该就是先乘以一个旋转矩阵，所得结果再乘以一个剪切矩阵 ( 1 1 1 0 ) ( ( 0 − 1 1 0 ) ( x y ) ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}(\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix}) (11​10​)((01​−10​)(xy​))

如果从总体角度上看，那么上面矩阵的效果或者说结果，应该和复合变换所对应的矩阵是一致的 ( 1 − 1 1 0 ) ( x y ) \begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix} (11​−10​)(xy​)

也即 ( 1 1 1 0 ) ( ( 0 − 1 1 0 ) ( x y ) ) = ( 1 − 1 1 0 ) ( x y ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}(\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix})=\begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix} (11​10​)((01​−10​)(xy​))=(11​−10​)(xy​)

约去等式相同部分，那么两者之积理应是相同的 ( 1 1 1 0 ) ( 0 − 1 1 0 ) = ( 1 − 1 1 0 ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}=\begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix} (11​10​)(01​−10​)=(11​−10​)

这两个矩阵的作用是需要从右往左看的，如下，可以理解为先 M 1 M_{1} M1​后 M 2 M_{2} M2​，矩阵 M 2 M_{2} M2​= ( 1 1 0 1 ) \begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix} (10​11​)作用于 M 1 M_{1} M1​的第一列得到 ( 1 1 ) \begin{pmatrix} 1\\ 1\end{pmatrix} (11​)，同样矩阵 M 2 M_{2} M2​= ( 1 1 0 1 ) \begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix} (10​11​)作用于 M 1 M_{1} M1​的第二列得到 ( − 1 0 ) \begin{pmatrix} -1\\ 0\end{pmatrix} (−10​)

其实，在实际计算中我们不用这么算，因为有一种普适性的方法可以计算出结果矩阵，也即

( a b c d ) ( e f g h ) = ( a e + b g a f + b h c e + d g c f + d h ) \begin{pmatrix} a & b\\ c & d\end{pmatrix}\begin{pmatrix} e & f\\ g & h\end{pmatrix}=\begin{pmatrix} ae+bg & af+bh\\ ce+dg& cf+dh\end{pmatrix} (ac​bd​)(eg​fh​)=(ae+bgce+dg​af+bhcf+dh​)

其实大家也能看到，这不就是我们熟知的矩阵乘法吗，但是我们的教育中太过重视怎么算的问题，但是怎么算根本就不是矩阵的本质的问题，它只是一种所谓的“技巧”，一种可以帮助你快速得到复合变换结果的计算方法，所以大家一定要明白矩阵乘法的本质，而不应该迷失在数字的世界中

我们都知道，矩阵是不满足交换律的，也即 A B ≠ B A AB\neq BA AB​=BA，那么为什么呢？在课本练习中，通常会采用代数运算的方法，通过上面的计算公式加以计算然后计算出它们不相等，其实这是根本没有必要的，因为这不是本质问题，这只是一种表示方式，没有说到问题的本质上

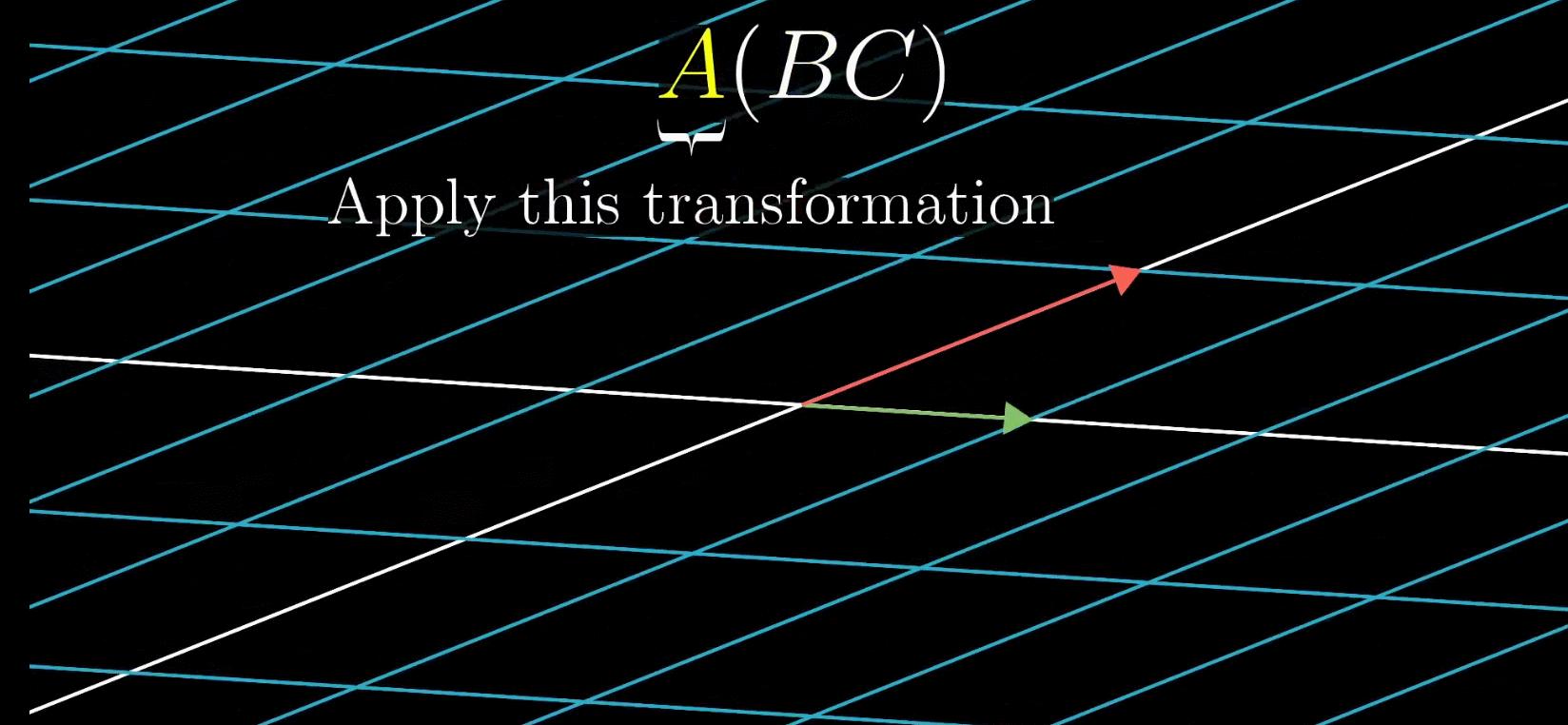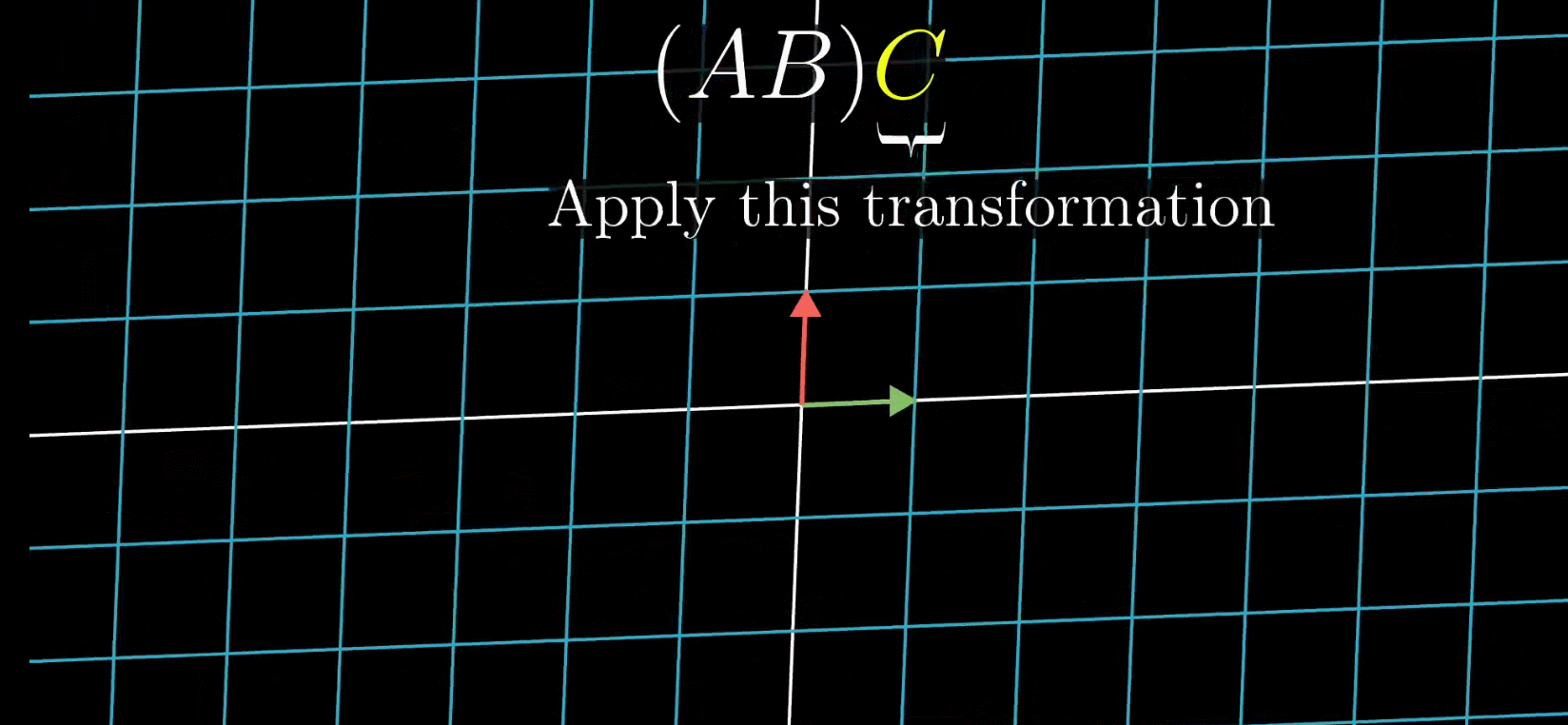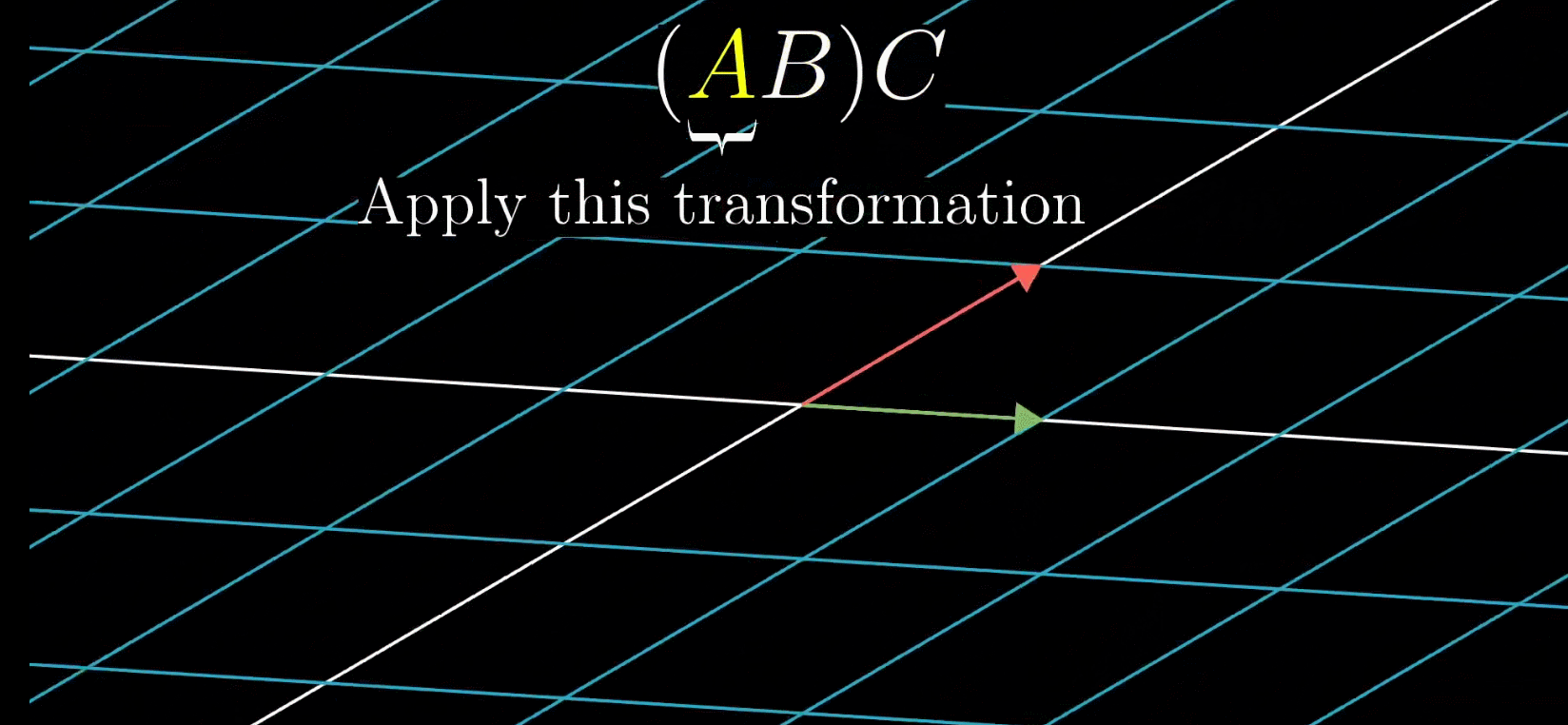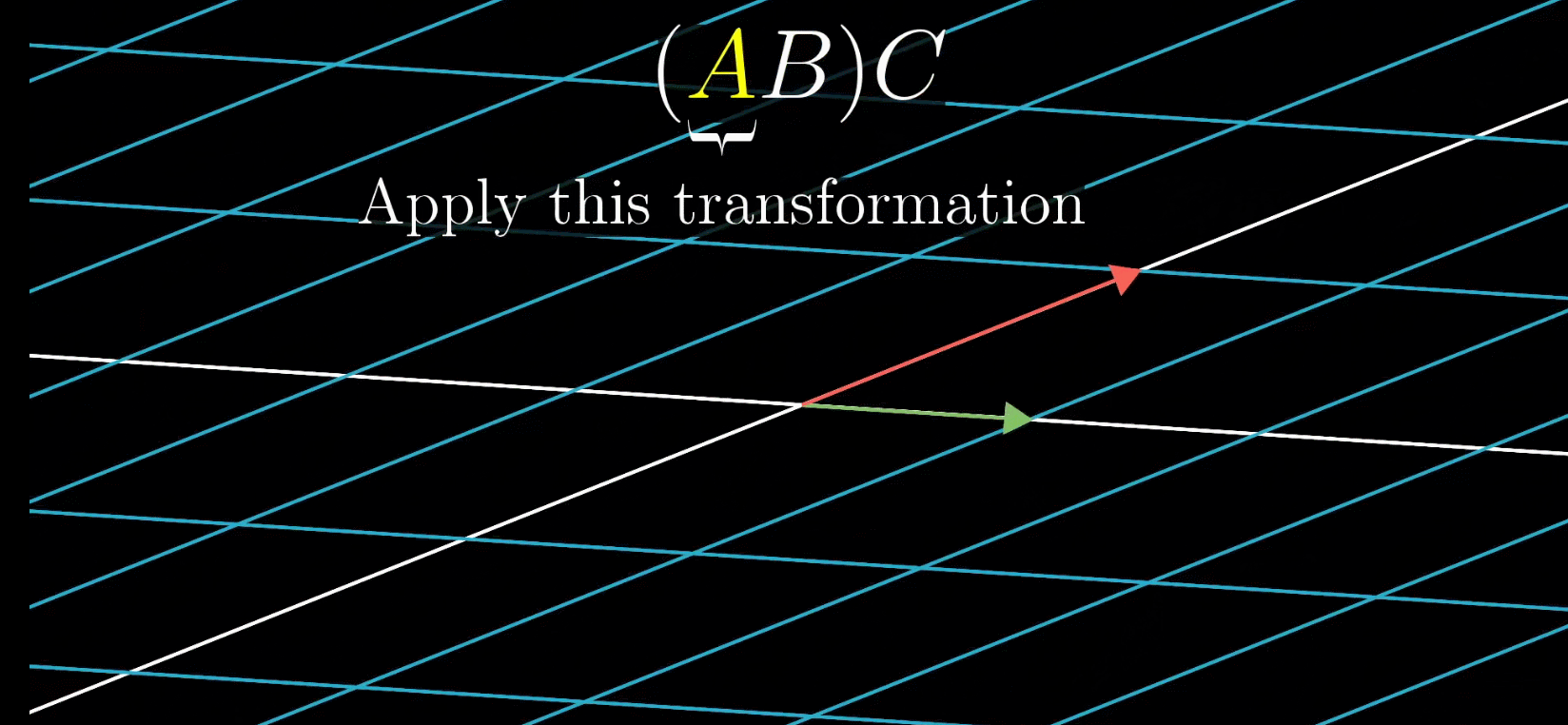
如果拿上面的例子，我们先左的是旋转再做的是剪切，对应的就是 M 2 M 1 M_{2}M_{1} M2​M1​，那么最终效果如下 如果做左剪切，再做旋转，也即 M 1 M 2 M_{1}M_{2} M1​M2​，最终效果如下

大家可以发现最终效果完全不一致了，也就说这根本不是一个变换，自然也就不可交换

我们都知道，矩阵满足结合律，也即 ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)，那么为什么呢？ 这个其实就很明白了，因为在这种情况下无论你先计算AB然后再计算ABC，还是先计算BC然后再计算ABC，最终的变换效果是一致的，那么自然而然是满足结合律的。