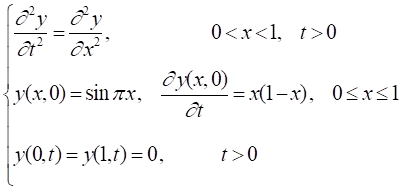五点差分法求解偏微分方程（PDE）

2023-10-05 09:10| 来源: 网络整理| 查看: 265

先以一个例题带大家了解五点差分法求解PDE

偏微分方程的解析解通常是非常难求的，即使是多数常微分方程，通常也难以计算解析解，即使可以计算，那也是相当复杂，因此，微分方程数值解的求解，是我们的一个重要的研究方向

求解微分方程数值解的核心，就是用差商来代替微商， $\Delta t,\Delta x$ 可以取一个比较小的值

$\frac{\partial y(x,t)}{\partial t}\approx\frac{y(x,t+\Delta t)-y(x,t)}{\Delta t}$

二阶向前差商

$\frac{\partial^2y(x,t)}{\partial\ t^2\ }\approx\frac{\frac{\partial y(x,t+\Delta t)}{\partial\ t}-\frac{\partial y(x,t)}{\partial\ t}}{\Delta t}$

$\approx\frac{\frac{y\left(x,t+\Delta t+\Delta t\right)-y\left(x,t+\Delta t\right)}{\Delta t}-\frac{y\left(x,t+\Delta t\right)-y\left(x,t\right)}{\Delta t}}{\Delta t} \\ =\frac{y\left(x,t+2\Delta t\right)-2y\left(x,t+\Delta t\right)+y\left(x,t\right)}{\left(\Delta t\right)^2}$

二阶向后差商

$\frac{y\left(x,t\right)-2y\left(x,t-\Delta t\right)+y\left(x,t-2\Delta t\right)}{\left(\Delta t\right)^2}$

二阶中心差商

$\frac{y\left(x,t+\Delta t\right)-2y\left(x,t\right)+y\left(x,t-\Delta t\right)}{\left(\Delta t\right)^2}$

差商有多种形式，我们选择中心差商

同理，y对x的二阶中心差商

$\frac{y\left(x+\Delta x,t\right)-2y\left(x,t\right)+y\left(x-\Delta x,t\right)}{\left(\Delta x\right)^2}$

由题目条件

$y(x,0)=sin\pi x,y(0,t)=y(1,t)=0$

可以确定边界取值，这是Dirchilet边界条件

下图是Dirchilet边界条件的直观解释，绿色点代表已知点。

由题目条件

$\frac{\partial y\left(x,0\right)}{\partial t}=x\left(1-x\right),0\le x\le1$

可以确定 $(x,0)$ 附近点的取值，这是Neumann边界条件

用差分可以近似表示成

$\frac{y\left(x,\Delta t\right)-y\left(x,0\right)}{\Delta t}=x\left(1-x\right),0\le x\le1$

下图是Neumann边界条件的直观解释，灰色点代表其他已知点，绿色点代表Neumann边界条件确定的点。

由题目条件

$\frac{\partial^2y}{\partial x^2}=\frac{\partial^2y}{\partial t^2},0\le x\le1,t0$

可以得出 $y\left(x,t+\Delta t\right),y\left(x,t\right),y\left(x,t-\Delta t\right),y\left(x+\Delta x,t\right),y\left(x-\Delta x,t\right)$ 的近似关系

$y\left(x,t+\Delta t\right)=2y\left(x,t\right)-y\left(x,t-\Delta t\right)+\frac{\left(\Delta t\right)^2}{\left(\Delta x\right)^2}\left(y\left(x+\Delta x,t\right)-2y\left(x,t\right)+y\left(x-\Delta x,t\right)\right),(\ast)$