| 学习姿态解算的笔记(包括四元数和融合算法) | 您所在的位置:网站首页 › 图像融合原理与算法的关系 › 学习姿态解算的笔记(包括四元数和融合算法) |
学习姿态解算的笔记(包括四元数和融合算法)
|
参考资料: 姿态解算简介 Craze维基百科 Mahony互补滤波算法 Craze维基百科 卡尔曼滤波 B站 IMU Data Fusing: Complementary, Kalman, and Mahony Filter 四元数解算姿态完全解析及资料汇总 百度文库 文章目录 如何表示姿态如何表示旋转的信息欧拉角定义分类表示 矩阵四元数如何表示旋转呢? 为何要使用四元数来保存姿态信息三者之间的关系转化中需要注意的区别 怎么从原始数据得到四元数数据融合Mahony算法卡尔曼滤波方差和协方差状态观测器卡尔曼滤波的作用卡尔曼滤波应用 如何表示姿态我们可以利用旋转来描述物体的姿态,因此我们保存旋转的信息。 旋转指的是两个坐标系之间的变换关系。 欧拉角:由三个角度组成,在特定坐标系下用于描述刚体的姿态(orientation). 简单来说,就是绕一个三维坐标系统下的三个基轴旋转三个角度,可以用来表示物体通过各种绕七绕八的转,最终转到某种形态。 分类欧拉角按旋转的坐标系分为内旋(intrinsic rotation)和外旋(extrinsic rotation)。 按旋转轴分为经典欧拉角(Proper Euler Angle)和泰特布莱恩角(Tait–Bryan angles)。 经典欧拉角(Proper Euler Angle):按(z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)轴序列旋转,即第一个旋转轴和最后一个旋转轴相同。 泰特布莱恩角(Tait–Bryan angles):按(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)轴序列旋转,即三个不同的轴 。 表示具体可以用 (φ, θ, ψ)(轴序,旋性)来描述一个欧拉角。 规定旋转正负,旋转顺序和旋转参照的坐标系十分重要,三个条件有一个不同,就可能导致用来表示相同姿态的一组欧拉角不同。而这种不同会导致通过四元数转化得来的欧拉角错误。因为不同顺序的旋转产生的欧拉角是不同的。 yaw-pitch-roll(heading-pitch-bank) 我们把(z,y,x 内旋(intrinsic))的这种格式称为 yaw-pitch-roll(heading-pitch-bank), 常应用于飞行器。注意,yaw-pitch-row 是针对飞行器的概念。 与之(内旋特性)对应的是用欧拉角表示的方向余弦矩阵 DCM 的求法:三个单轴 DCM 左连乘。
如何理解3D动画中的欧拉角以及死锁?知乎-马同学 矩阵
用相对运动和极坐标来证明会简单许多。也可以用平面几何(具体参见第二条链接) 方向余弦矩阵描述的是 坐标系的旋转。 四元数如何表示旋转呢?
Q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
Q = q_0 + q_1i + q_2j + q_3k
Q=q0+q1i+q2j+q3k 单位四元数描述的是 矢量的旋转。 为何要使用四元数来保存姿态信息运算量小。 三者之间的关系 使用四元数来保存飞行器的姿态(也就是在地球坐标系中的俯仰/横滚/航向情况)。在需要控制的时候,会将四元数转化为欧拉角,然后输入到姿态控制算法中。 而矩阵是工具(四元数,欧拉角)的工具,它表示坐标系变换提供了便利。而变换矩阵的元素可以是四元数的 q 1 , q 2 , q 3 , q 4 q_1, q_2, q_3, q_4 q1,q2,q3,q4,也可以是欧拉角正余弦。 求出的四元数已经唯一对应了一种姿态,而用来表示这种姿态的三个欧拉角(绕x,绕y,绕z)会因为顺规的不同而不同,反映在矩阵上就是余弦矩阵不同。
R R R 是从欧拉角定义出发推出来的DCM,元素由欧拉角三角函数表示。 这两个矩阵表示同一个变换,而且都是正交阵,所以两个矩阵相等,对应的元素也相等。由此得到欧拉角与四元数系数之间的关系。 转化中需要注意的区别 变换矩阵有一个很神奇的特性。 它既可以表示坐标系的旋转,也就是通常所说的坐标系变换,然后用来求某个固定向量在新坐标系下的新坐标。(这是转换矩阵在姿态解算中矫正步骤用到的含义。) 能同时它表示,坐标系不变下向量的旋转,然后用来求旋转之后向量的新坐标。(这是四元数所表达的含义。) 旋转是相对的,矩阵表示的含义取决于我们的观察角度。 怎么从原始数据得到四元数 调整单位 积分 龙格-库塔法或者毕卡法 陀螺仪原始数据 角速度 偏转角度 四元数
测量误差 v k v_k vk ~ N ( 0 , Q ) N(0, Q) N(0,Q)
但 这 时 候 我 们 得 到 四 元 数 只 用 到 了 陀 螺 仪 的 数 据 。 但这时候我们得到四元数只用到了陀螺仪的数据。 但这时候我们得到四元数只用到了陀螺仪的数据。 数据融合 Mahony算法 角速度w 四元数Q 坐标系变换矩阵 推算估计值g^ 加速度计测得的g err err & Ierr 陀螺仪器 毕卡法或龙格库塔法 p' = qpq*改写成矩阵乘法 左乘世界坐标系下的重力坐标 +-- acc Ki Kp 卡尔曼滤波 方差和协方差我们如何衡量数据的可靠程度呢?使用方差或协方差。 协方差的大小既受两个随机变量各自的方差的影响,也受两个两个随机变量相关性的影响。而在卡尔曼滤波当中,我们主要用到协方差的第一个性质。 记住,
x
x
x 是我们想要的,而
y
y
y是我们能测到的 这里有一种粗略的转换关系可以帮助理解。 x ′ = A x + B x' = Ax + B x′=Ax+B lim Δ t − > 0 x ( t + Δ t ) − x ( t ) Δ t = A x ( t ) + B \lim_{\Delta t->0}\frac{x(t+\Delta t)-x(t)}{\Delta t} = Ax(t)+B Δt−>0limΔtx(t+Δt)−x(t)=Ax(t)+B 假设 Δ t \Delta t Δt很小,那么有 x ( t + Δ t ) = ( A Δ t + 1 ) x ( t ) + B Δ t x(t+\Delta t)=(A\Delta t+1)x(t)+B\Delta t x(t+Δt)=(AΔt+1)x(t)+BΔt x k = A ′ x k − 1 + B ′ x_{k}=A'x_{k-1}+B' xk=A′xk−1+B′
状态观测器不考虑噪声,要求系统可检测,并且增益通常是时不变的。 而卡尔曼滤波则详细考虑了噪声和初始估计误差,智能的计算每一步的增益,以达到对状态的最优的估计。 测量误差
v
k
v_k
vk ~
N
(
0
,
Q
)
N(0, Q)
N(0,Q)
在算法的最开始,预估值 x ^ k − 1 \hat{x}_{k-1} x^k−1 和 P k − 1 P_{k-1} Pk−1 值来自初始估计值。 在更新步骤,算法使用在预测步骤中计算得到的预估值,计算并更新后验估值和误差协方差。 调整卡尔曼增益,使更新后的状态值误差协方差最小。 如果使用卡尔曼滤波来融合陀螺仪和加速度计,那么实际上就是将陀螺仪的输出作为系统的增量预测,姿态增量方程就是卡尔曼的状态方程(其实就是四元数微分方程),然后从加速度计获得重力加速度作为观测值,然后运用卡尔曼滤波进行融合。 |
【本文地址】




 (进一步可探究如何证明)
(进一步可探究如何证明) C
b
R
C_b^R
CbR 是从四元数推出来的DCM,元素由四元数的系数表示;
C
b
R
C_b^R
CbR 是从四元数推出来的DCM,元素由四元数的系数表示; 过程误差
w
k
w_k
wk ~
N
(
0
,
R
)
N(0, R)
N(0,R)
过程误差
w
k
w_k
wk ~
N
(
0
,
R
)
N(0, R)
N(0,R)
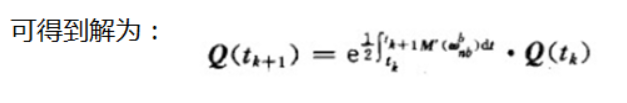



 线性系统,可以用一阶线性微分方程描述。 不连续的系统,可以用差分方程描述,其实就是递推式。
线性系统,可以用一阶线性微分方程描述。 不连续的系统,可以用差分方程描述,其实就是递推式。 解一下一阶线性微分方程。
解一下一阶线性微分方程。 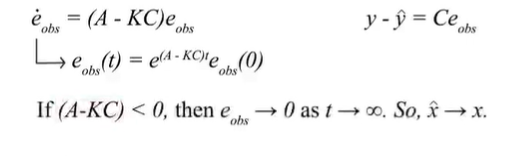
 过程误差
w
k
w_k
wk ~
N
(
0
,
R
)
N(0, R)
N(0,R)
过程误差
w
k
w_k
wk ~
N
(
0
,
R
)
N(0, R)
N(0,R)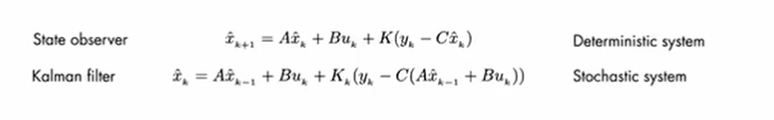

 在预测部分,系统模型用于计算状态预估值和误差协方差P,对于单状态系统,P是状态预估值的方差,可以把它当作预测状态中的不确定性的度量。这种不确定性来自过程噪声和预估值
x
^
k
−
1
\hat{x}_{k-1}
x^k−1 的不确定性的影响。
在预测部分,系统模型用于计算状态预估值和误差协方差P,对于单状态系统,P是状态预估值的方差,可以把它当作预测状态中的不确定性的度量。这种不确定性来自过程噪声和预估值
x
^
k
−
1
\hat{x}_{k-1}
x^k−1 的不确定性的影响。