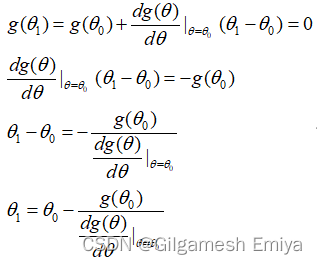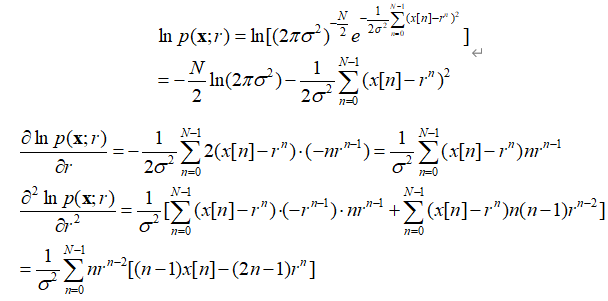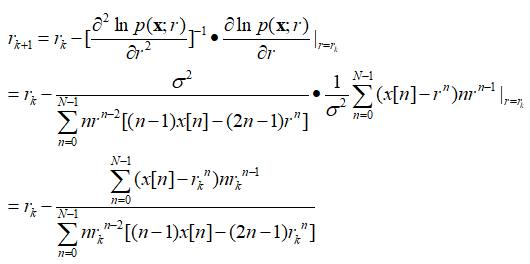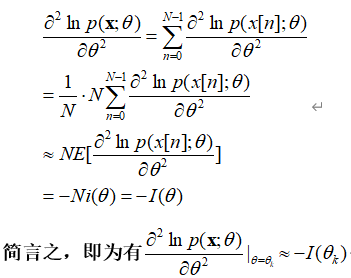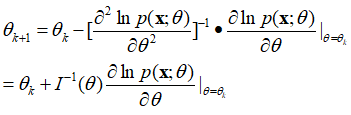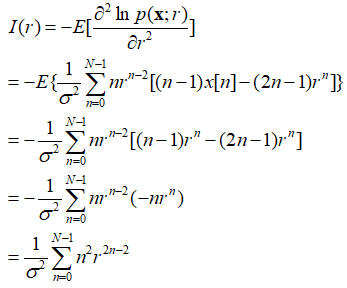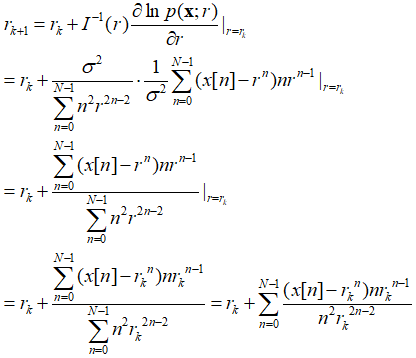MLE的数值确定：Newton

您所在的位置：网站首页 › latticeeasy › MLE的数值确定：Newton

MLE的数值确定：Newton

2023-06-21 17:18| 来源: 网络整理| 查看: 265

本篇随笔主要参考Steven M. Kay的《Fundamentals of Statistical Signal Processing: Estimation Theory》第七章节最大似然估计，用作为平时的学习记录。在此我们主要来分析两种迭代算法，即Newton-Raphson迭代法和得分法。相对于K的论述，本文在此补充了一些详细的推理过程和计算步骤。

MLE的一个独特的优点在于对于一个给定的数据集，总能在数值上求出他。(因为当一个已知函数即似然函数取最大值时，MLE就可确定下来)。

如果的θ可允许范围在区间[a,b]中（控制在有限区间内），那么只需在此区间上使得p(x;θ)最大即可，采用网络搜索法；（对于给定的数据集，只要θ 值的间隔足够小，我们就保证可求出其MLE；当然对于一个新的数据集，因为似然函数肯定会改变，所以将不得不重复使用网格搜寻法）

remark：有些情况下我们很难知道似然函数和参数θ之间函数是什么样的，参数的取值范围、似然函数关于参数θ的单调性、极值、最值等可能会很复杂难以把握。

如果θ的范围没有控制在有限范围内，那么从数值计算角度来看，网络搜索法也许是不可行的，这种情况下可通过迭代法求最大值。此处的迭代法可以理解为一种数值最大化的技术。迭代法也存在一些问题：如果设定的初始值接近于真实最大值，那么这些方法可求出MLE，否则迭代就不会收敛，或者只会收敛到局部最大值，即事先不知道它们是否收敛，收敛的话所求的是否为MLE。

先给出问题模型：WGN中的指数信号

观测数据为 $x[n]=r^{n}+w[n],n=0,1,...,N-1$ （其中w[n]是均值为0方差为 $\sigma ^{2}$ 的WGN）待估计量为参数r，即指数因子(r>0)，r的MLE就是使似然函数最大的r值。

概率密度函数（PDF）为： $p(\mathbf{x};r)=\frac{1}{(2\pi \sigma ^{2})^{\frac{N}{2}}}exp[-\frac{1}{2\sigma ^{2}}\sum_{n=0}^{N-1}(x[n]-r^{n})^{2}]$

等效为使式子 $J(r)=\sum_{n=0}^{N-1}(x[n]-r^{n})^{2}$ 最小的r值。

对于J(r)求导，并令它等于零，

$\frac{\partial J(r)}{\partial r}=\sum_{n=0}^{N-1}2(x[n]-r^{n})\cdot [-nr^{n-1}]=0$

即

$\sum_{n=0}^{N-1}(x[n]-r^{n})nr^{n-1}=0$

这是一个r的非线性方程，不能直接求解。

接下来以Newton-Raphson法、得分法两种迭代法入手解决该例题。（一般还会介绍EM数学期望最大算法，本文暂且不做介绍）

一、Newton-Raphson迭代法：

通过求导函数的零值而使对数似然函数最大，

$\frac{\partial ln(\mathbf{x};\theta )}{\partial \theta }=0$ (7.26)

接着，使用迭代方法求解此方程，令 $g(\theta )=\frac{\partial ln(\mathbf{x};\theta )}{\partial \theta }$

同时，假设我们有一个求解(7.26)式的初始猜测值，将该初始猜测值称为θ0。因此，如果g(θ)在θ0附近是近似线性的，我们就能将它近似表示为

$g(\theta )\approx g(\theta _{0})+\frac{dg(\theta )}{d\theta}|_{\theta =\theta _{0}}(\theta -\theta _{0})$

remark：对于该式，我们要联想到高等数学中的微分思想来理解。

利用上式，求解零值所对应的θ1.（因此，令g(θ1)=0并解出θ1），具体计算步骤如下，

利用这个新的猜测值θ1作为线性化点，对函数g在此进行线性化，并重复前面的方法来求新的零值。这个猜测值序列将收敛到g(θ)的真零值。

总而言之，Newton-Raphson迭代法是根据前一个猜测值 $\theta _{k}$ ，利用下式求出新的一个猜测值 $\theta _{k+1}$ 。

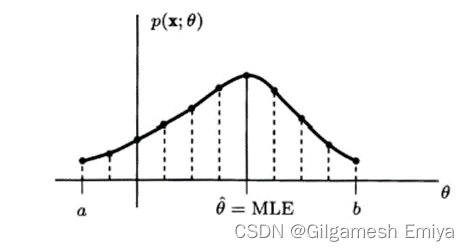
我们可以参考下图以便有更为直观的理解。（tag：上述数学式子中的dg(θ)/dθ即为下图中两个theta之间的斜率，从图中我们可以发现随着不断迭代，斜率越来越小、函数曲线越来越趋向于水平，我们越来越能够逼近所谓的真零值）

正如所期望的，迭代在 $\theta _{k+1}=\theta _{k}$ 处收敛，并且根据上式和 $g(\theta _{k})=0$ ，我们可计算得MLE，

注意：关于Newton-Rapson迭代法我们还需注意两点。一是，迭代可能不收敛(修正项的起伏可能很大)；二是，即使迭代收敛，求得的点也可能不是全局的最大值，而可能只是一个局部的最大值或者甚至是一个局部最小值(此情况可考虑采用多个起始点)。

在上述问题模型“WGN中的指数信号”中应用Newton-Rapson方法（具体计算步骤如下）：

先计算处对数似然函数及其关于参数r的一阶、二阶导数，

代入上述通过Newton-Rapson法求得MLE的公式中，求得带估计参数r的MLE，

二、得分法

事实上，对于独立同分布(IID)样本，根据大数定理(此处指的是辛钦大数定理)，对数似然函数对参数的二阶求导可近似约等于负的Fisher信息矩阵。具体如下。

首先，我们说明辛钦大数定理：

设随机变量 $X_{1},X_{2},...,X_{n},...$ 相互独立，服从同一分布且具有数学期望 $E(X_{k})=\mu (k=1,2,...)$ ，则序列 $\bar{X}=\frac{1}{n}\sum_{k=1}^{n}X_{k}$ 依概率收敛于 $\mu$ ，即 $\bar{X}\overset{P}{\rightarrow}\mu$ .

套用辛钦大数定理， $\frac{\partial ^{2}ln(x[n];\theta )}{\partial\theta ^{2}}$ 相互独立，服从同一分布且具有数学期望 $E(\frac{\partial ^{2}ln(x[n];\theta )}{\partial\theta ^{2}})$ ，则有 $\frac{1}{N}\sum_{n=0}^{N-1}\frac{\partial ^{2}ln(x[n];\theta )}{\partial\theta ^{2}}\overset{P}{\rightarrow}E(\frac{\partial ^{2}ln(x[n];\theta )}{\partial\theta ^{2}})$ .