| 【OI 组合数学】一看到排列组合就头晕?更适合Oier的《组合数学知识简明大全》 | 您所在的位置:网站首页 › 排列组合方法归类大全图片 › 【OI 组合数学】一看到排列组合就头晕?更适合Oier的《组合数学知识简明大全》 |
【OI 组合数学】一看到排列组合就头晕?更适合Oier的《组合数学知识简明大全》
|
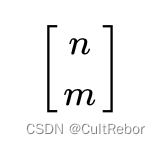
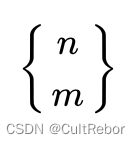
配合了情景、应用、真题、大量的公式干货以及简明的证明,为了方便阅读。有些生僻冷门的没有加进来希望大家谅解。 一到四属于基础内容,大佬们可以从五开始看 用尽心血整理的、公式全部手打出来的一篇博客,希望大佬能支持一下QAQ 废话不多说我们这就开始—— 一、加法原理加法原理的核心是分类。如果完成一件事情有\(n\)类方法,每一类方法数分别为\(A1,A2, … ,An\),则完成这件事一共有\(\sum_{i = 1}^{n}Ai\)种方法。 需要注意的是,每一类方法都可以独立完成事件。 二、乘法原理乘法原理的核心是分步。如果完成一件事情有\(n\)个步骤,每一个步骤数分别为\(B1,B2, … ,Bn\),则完成这件事一共有\(\prod_{j = 1}^{n}B_j\)种方法。 加法分类,类类独立;乘法分步,步步相关。 三、容斥原理为使两个集合重叠部分不被重复计算,先列出包含的所有对象的元素,然后再把重复的元素排除出去,使得计算的结果既无遗漏又无重复,称为容斥原理。 如果被计数的事物有\(A、B、C\)三类,则 \[A\cup B\cup C=A+B+C-A\cap B-B\cap C-C\cap A+A\cap B \cap C \]四、排列组合 \[n!=\prod_{i =0}^{n-1}(n-i)= n\times(n-1)\times(n-2)…\times2\times1 \]1.排列与排列数排列的定义:从\(n\)个不同元素中, 任取\(m\)个元素, 按照⼀定的顺序排成⼀列, 叫做从\(n\)个不同元素中取出\(m\)个元素的⼀个排列 排列数的定义:一个序列的有多少种给定的排列方法。 排列数公式: \[A_n^m = P_n^m =\prod_{i =0}^{m-1}(n-i)= n(n-1)(n-2)…(n-m+1) = \frac{n!}{(n-m)!} \]特别的,当 \(n=m\) 时,我们称之为全排列,i.e. 一个序列中所有元素的排列。 全排列数公式: \[A^n_n = P^n_n ==\prod_{i =0}^{n-1}(n-i)= n\times(n-1)\times(n-2)…\times2\times1 =n! \]1.组合与组合数组合的定义:从\(n\)个不同元素中, 任取\(m\)个元素, 并成一组, 叫做从\(n\)个不同元素中取出\(m\)个元素的⼀个组合 组合数的定义:一个序列的有多少种给定的组合方法。 组合数公式: \[C_n^m =\frac{A^m_n}{A^m_m}=\frac{\prod_{i =0}^{m-1}(n-i)}{\prod_{j =0}^{m-1}(m-j)}= \frac{n(n-1)(n-2)…(n-m+1)}{m!} = \frac{n!}{m!(n-m)!} \]与顺序有关的为排列问题,与顺序无关的为组合问题。 五、特殊的排列组合 1.圆排列 意义:从 \(n\) 个元素的序列 \(A[n] = { a_1, a_2, a_3, ......, a_n }\) 中,取出 \(r\) 个元素排列成一个圆,求使得不同的圆排列的排列数,e.g. turn to [1] [1][2][3][4][5][6] =========> [5] [2] (n = 6, r = 5) [4] [3] 一种圆排列如从 6 个元素的序列 \(A[6] = {1, 2, 3, 4, 5, 6}\) 中,取出 5 个元素排列成不同的圆,不同圆的数量即圆排列排列数。 公式:圆排列排列数公式为: \[\frac{A_{n}^{r}}{r}(r,n\in N^*;r\in [1,n]) \]先将所有元素全排列,得公式的分子。 但是我们发现,每次 \(r\) 个不同元素打头形成的序列、尽管线性观察时是不一样的。但变成圆排列时就变成了完全相同的重复情况,i.e. [1][2][3][4][5] [1][2][3][4][5] [2][3][4][5][1] is same as [1][2][3][4][5] [3][4][5][1][2] [1][2][3][4][5] [4][5][1][2][3] [1][2][3][4][5] [5][1][2][3][4] [1][2][3][4][5] 这是重复的排列方式中的1/5(上图左边矩阵中第一列是1 2 3 4 5哦) 所以我们要除以不同元素打头形成的圆排列相同的序列数,也就是在分子的基础上除于 \(r\) 。 特别地,当 \(n = r\) 时,i.e. \(n\) 个元素全部用来圆排列时,圆排列公式可这样转化: \[\frac{A_{n}^{n}}{n} = \frac{n!}{n} = \frac{n \times (n - 1) \times(n - 2)\times…\times1}{n} = (n - 1)!(n\in N^*) \]例题: 1.[***真题] 在 NOI 期间,主办单位为了欢迎来自各国的选手,举行了盛大的晚宴。在第十八桌,有5名大陆选手和5名港澳选手共同进膳。为了增进交流,他们决定相隔就坐,即每个大陆选手左右旁都是港澳选手,每个港澳选手左右旁都是大陆选手。那么,这一桌一共有多少种不同的就坐方案?注:如果在两个方案中,每个选手左右相邻的选手相同,则视为同一种方案。 解析:定义座位如 \(A a B b C c D d E e\) ,其中大写字母所在位置坐大陆选手,小写字母所在位置坐港澳选手,先考虑大陆选手圆排列入座,排列方案为 \(\frac{5 ! }{5}\),港澳选手再插空全排列,排列数乘上 5! 。 答案: \[\frac{5!}{5}\times5! = 4!\times5! = 2880 \]2.[*****] 建议了解一下破环为列的算法,虽然与圆排列数没有啥大关系。 2.有重复元素的全排列 意义:请看一个特殊的序列:\(A[6] = {1, 1, 3, 3, 3, 3}\) 。把这个序列排成一排,有多少种排列方法。 不难看出这个序列中有 2 个重复的元素 1,4 个重复的元素 3。 从每个局部元素单独考虑很让人头大,不妨由整体到局部,先把这 6 个元素的全排列数求出,i.e. \[(4 + 2)! = 6! \]反思这么考虑的代价:我们考虑了整体序列中 6 个元素的全排列数,也就是无视了元素与元素之间的顺序关系,但 2 个 1 之间的排列顺序改变,不会影响整个序列的排列数,同样 4 个 3 之间也是,所以要在之前的结果上、除以每组相同元素之间的全排列数,i.e. \[\frac{(4+2)!}{4!\times2!} = \frac{6\times5\times4\times3\times2\times1}{2\times1\times4\times3\times2\times1} = 15 \]公式:拓展到一般,那么假设一个序列种有 \(k\) 组相同的元素,第 \(i\) 组相同的元素数量为 \(n_i\),则有重复元素的全排列数 i.e. \[\frac{(\sum_{i = 1}^{k}n_i)!}{\prod_{j = 1}^{k}n_j!}=\frac{(n_1+n_2+n_3+…+n_k)!}{n_1!\times n_2!\times n_3!\times …\times n_k!}(k\in N^*) \]例题: 1.[*] 有3个相同的黄球、2个相同的蓝球、4个相同的白球排成一排,问:有多少种不同的排法? \[\frac{(3+2+4)!}{(3!\times2!\times4!)}=1260 \]2.[****] 把两个红球、一个蓝球、一个白球放到10个编号不同的盒子中去,每个盒子最多放1个球,有多少种放法? \[\frac{A_{10}^{4}}{2!\times1!\times1!}=2520 \]3.[**真题] 将N个红球和M个黄球排成一行。例如:N=2,M=2可得到以下6种排法: 红红黄黄 红黄红黄 红黄黄红 黄红红黄 黄红黄红 黄黄红红 问题:当N=4,M=3时有多少种不同排法?(不用列出每种排法) \[\frac{(4+3)!}{4!\times3!} = 35 \]4.[*****真题] 由3个a,5个b和2个c构成的所有字符串中,包含子串“abc”的共有( )个。 A. 40320 B. 39600 C. 840 D. 780 E. 60至少有1个\(“abc”\)的组合:\(\frac{8!}{(1!\times 2!\times4!\times1!)} = 840\) 分子的 8 i.e. \(“abc, a, a, b, b, b, b, c”\),把\(“abc”\)捆绑在一起 确定有2个\(“abc”\)的组合:\(\frac{6!}{(2!\times1!\times3!\times 0!)} = 60\) 减去因排列顺序而重复的组合:\(840 – 60 = 780\) 3.不相邻组合 意义:请继续看这样一个序列 \(A[6] = {1, 2, 3, 4, 5, 6}\),我们要求从中取出 3 个元素组成一个组合,使得里面有 1 没有 2,有 2 没有 1 或 3,有 3 没有 2 或 4,有 4 没有 5 或 6,有 6 没有 5。这种有你没我有我没你不是你死就是我亡的组合叫做不相邻组合。而样例中的不相邻组合有 {1, 3, 5}、{1, 3, 6}、{1, 4, 6} 和 {2, 4, 6} 四种。 公式:由样例拓展出去,不相邻组合就是从一个有 \(n\) 个元素的序列中、取 \(r\) 个不相邻的数进行组合(不可重)。i.e. 使得所取任一组合中的任一元素 \(a_i \not= a_{i+1}\)。其组合数为: \[C_{n-r+1}^{r}(r,n\in N^*;r\in [1,n]) \]比较容易得出,请读者自行推导(只要分类讨论、一个隔一个列举就能找到规律)。 例题: 1.[**] 书架上有21本书,编号从1到21,从其中选4本,其中每两本的编号都不相邻的选法一共有多少种? \[C^{4}_{18} = 3060 \]2.[****] 7个同学围坐一圈,要选2个不相邻的作为代表,有多少种不同的选法? \[C^2_6 - 1 = 14 \]4.有重复元素的组合 意义:现在有 3 个相同的小球,把它们放到 2 个不同的盒子里,可以考虑板插法。 但是不要忘了,题目中没说不能有空盒子,所以我们要补上两个假球,当作真球来板插分组: 球 | 球 | 球 假球 假球 球 | 球 球 | 假球 假球 球 | 球 球 假球 | 假球 球 球 | 球 | 假球 假球 球 球 | 球 假球 | 假球 球 球 球 | 假球 | 假球于是答案就是 \(C^{2}_{3+2-1} = C^2_4 = 6\) 。 公式:拓展为:从有 \(n\) 个不同的元素的序列中取 \(r\) 个的元素的组合数,允许序列中有重复元素,允许有空的组合: 你还不会板插法嘛?公式呼之欲出: \[C^r_{n+r-1}(r,n\in N^*;r\in [1,n]) \]例题:样例当例题也够了。死记硬背公式的话注意与不相邻组合的区分,但是不建议死记硬背。 5.错位排列 意义:错位排列问题,又称伯努利-欧拉装错信封问题。 摆在\(zyh\)面前有编号是 \(1、2、… 、n\) 的 \(n\) 封寄给\(syy\)干爹的信,把它们装入编号为 \(1、2、… 、n\) 的 \(n\) 个信封,要求每封信和信封的编号不同,问有多少种装法? 公式:设 \(a_1, a_2, … , a_n\) 是 \(A[n]\) 的一个全排列,若对于任意的 $ i\in [1, n]$ , 都有 \(a_i \not= A[i]\),则称 \((a_1, a_2, … , a_n)\) 是 \(A[n]\) 的一个错位排列。 一般用 \(Dn\) 表示 \(A[n]\) 的错位排列的个数。 推导很困难,我们不妨试试把前几种情况列出来哦 当 \(n = 1\) 时,显然没有错位装法,或者0种; 当 \(n = 2\) 时,有 (2, 1) 共1种装法; 当 \(n = 3\) 时,有 (2, 3, 1)、(3, 1, 2) 共2种装法; 当 \(n = 4\) 时,有 (2, 1, 4, 3)、(3, 1, 4, 2)、(4, 1, 2, 3)、(3, 4, 1, 2)、(2, 4, 1, 3)、(4, 3, 1, 2)、(4, 3, 2, 1)、(2, 3, 4, 1)、(3, 4, 2, 1) 共 9 种装法。 错位排列前若干项的值为:0,1,2,9,44,265,...... 要不……我先给出公式 递推公式: \[D(x) = \begin{cases}x & (x = 0 \wedge x = 1)\\(x - 1)\times[D(x - 1)+D(x - 2)] & (x\in N^*,x \not=0 \vee x\not=1)\end{cases} \]通项公式: \[D(n) = n!\times[\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}+…+(-1)^n\frac{1}{n}] = n!\times\sum_{i = 2}^n\frac{(-1)^i}{i}(n\in N^*) \]推导:设 \(D(n)\) 为 \(n\) 个不同元素的错排方案。 第一部分: \(n\) 先不动,把另外的 \(n - 1\) 个数错排,方案是:\(D(n - 1)\),然后 \(n\) 和另外的 \(n - 1\) 个每一个交换,共有 (\(n - 1) \times D(n - 1)\)种方案。 第二部分: \(n\) 和其他的 \(n - 1\) 个之一交换,其余的 \(n - 2\) 个错排,共有\((n-1)(n-2)\)种方案。 由加法原理得出递推公式 6.球盒问题 球 (数量为\(k\)) 盒 (数量为\(n\)) 盒是否可空 公式 1 相同 不同 否 \(C_{n - 1}^{k-1}\) 2 相同 不同 是 \(C_{n +k- 1}^{k-1}\) 3 相同 相同 否 $ S(n,k)$ 4 相同 相同 是 \(S(n+k, k)\) 5 不同 相同 否 \(S(n,k)\) 6 不同 相同 是 \(\sum^k_{i=1}S(n,i)\) 7 不同 不同 否 \(S(n,k)\times k!\) 8 不同 不同 是 \(k^n\) 球相同,盒不同,且盒子不能空等价于“正整数的有序拆分”。 经典插板法,把\(r\)个球排成一排,然后每隔一段在两个球之间插入一个插板,这样一排球就会变成有序(盒子不同)的几份。\(n\)个球对应\((n-1)\)个空隙,\(k\)个盒子对应\((k-1)\)个插板,题目就变成从\((n-1)\)个空隙中选\((k-1)\)个位置插入插板,即 \(C_{n - 1}^{k-1}\)。 球相同,盒不同,且盒子可以空等价于“求方程\(x_1+x_2+…+x_k=n\)的非负整数解”。 类似1的做法,既然可以空,那么把每个盒子先补上一个球,题目就变成\((n+k)\)个球和\(k\)个盒子,且盒子不能空的情况,即 \(C_{n +k- 1}^{k-1}\)。 球相同,盒相同,且盒子不能空等价于“正整数的无序拆分”,即正整数\(n\)拆分成\(k\)份(没有先后顺序)的方法。 递推公式为: \(S(n,k) = S(n-1,k-1) + S(n-k,k)\) (至少有1份是1,或者每一份数量都大于1) 边界条件:\(S(n,1)=S(n,n)=1\),且当\(k>n\)时,\(S(n,k)=0\)。 球相同,盒相同,且盒子可以空等价于“非负整数的拆分”,可以先把每个盒子放上一个球,再按照3中的情况处理。 即计算 \(S(n+k, k)\)的值,或者计算 \(\sum_{i = 1}^k S(n,i)\)的值。 球不同,盒相同,且盒子不能空这是集合\(n\)的\(k\)部拆分问题。即将集合\(n\)拆分成\(k\)份,每份至少一个元素。 规定: 当\(n\in[1,k)时\),\(S(n,k)=0\) 当\(n\in[1,\infty)\)时,\(S(n,0)=S(0,n)=0\), 以及\(S(0,0)=0\) 则 \(S(n,k)= S(n-1,k-1) + k\times S(n-1,k)\) \((n,k \in N)\) 球不同,盒相同,且盒子可以空集合n的至多被拆分成k个分部的分拆。 公式: \(\sum_{i = 1}^k S(n,i)\) 球不同,盒不同,且盒子不能空这是集合n的k部有序拆分问题。 公式:\(k!\times S(n,k)\) 球不同,盒不同,且盒子可以空这是可重复排列问题。 公式:\(k^n\) 六、特殊的递推式 1.斐波那契(Fibonacci)其实一点也不特殊,我最多送你一个递推一个通项 \[F(n)=\begin{cases} 1&(n\in N^*,n\in(-\infty,2])\\ F(n-1)+F(n-2)&(n\in N^*,n\in[3,+\infty)) \end{cases} \]\[F(n)=\frac{({\frac{1+\sqrt5}{2}})^n-({\frac{1-\sqrt5}{2}})^n}{\sqrt5} (n\in N^*) \]2.斯特林数(Stirling)这类数不是很常用,甚至BFS(Baidu First Search)也无法直接搜到斯特林数的前几项。
1 1 1 2 3 1 6 11 6 1 24 50 35 10 1 120 274 225 85 15 1 720 1764 1624 735 175 21 1 5040 13068 13132 6769 1960 322 28 1 40320 109584 118124 67284 22449 4536 546 36 1 362880 1026576 1172700 723680 269325 63273 9450 870 45 1 \[S(n,m)=\begin{cases} 0&(n,m\in N^*;m>n)\\ 1&(n,m\in N^*;m = 1 \wedge m = n)\\ S(n-1,m-1)+S(n-1,m)\times (n-1)&(n,m\in N^*;n,m\in (1,+ \infty ))\\ \end{cases} \]\(n\)个不同元素分成\(m\)个不同的环的方案数(两个环不相同当且仅当这两个环不能通过旋转得到)
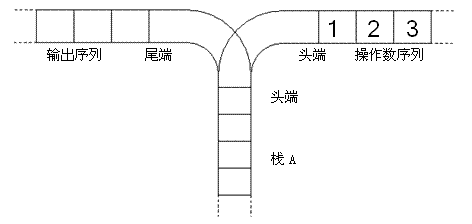
1 1 1 1 3 1 1 7 6 1 1 15 25 10 1 1 31 90 65 15 1 1 63 301 350 140 21 1 1 127 966 1701 1050 266 28 1 1 255 3025 7770 6951 2646 462 36 1 1 511 9330 34105 42525 22827 5880 750 45 1 \[S(n,m)=\begin{cases} 0&(n,m\in N^*;m>n)\\ 1&(n,m\in N^*;m = 1 \wedge m = n)\\ m\times S(n-1,m)+S(n-1,m-1)&(n,m\in N^*;n,m\in (1,+ \infty ))\\ \end{cases} \]\(N\)个不同元素分成\(m\)个不同的集合的方案数(集合非空) 情景一、放置小球\(n\)个有区别的球放到\(m\)个相同的盒子中,要求无一空盒,其不同的方案数用 \(S(n,m)\)表示,称为第二类\(Stirling\)数。 设有\(n\)个不同的球,分别用\(b1,b2,…,bn\)表示。 从中取出一个球\(bn\), \(bn\)的放法有以下两种: \(bn\)独自占一个盒子;那么剩下的球只能放在\(m-1\)个盒子中,方案数为 $S(n-1,m-1) $ \(bn\)与别的球共占一个盒子;那么可以事先将\(b1,b2,…,bn-1\)这\(n-1\)个球放入\(m\)个盒 子中,然后再将球\(bn\)可以放入其中一个盒子中 方案数为:\(m*S(n-1,m) S(n,m)=m*S(n-1,m)+S(n-1,m-1) (n>1,m>1)\) 边界条件:\(S2(n,1)=1;S2(n,n)=1;S2(n,k)=0(k>n)\) 划分方案数\(i.e.\)第二类斯特林数 情景二:集合划分问题。设\(S\)是一个包含\(n\)个元素的集合,\(S={b1,b2,b3,…,bn}\),现需要将\(S\)集合划分为\(m\)个满足如下条件的集合 \(S1,S2, …,Sm\); \(Si\not=\emptyset\); \(Si\cap Sj=\emptyset\); \(S1∪S2∪…∪Sm=S; (1\leq i , j\geq m)\) 则称\(S1,S2, …,Sm\)是\(S\)的一个划分。 1、输入n和m的值,输出不同的划分方案数。 要求:输入数据有一行,第一个数是n,第二个数m。 样例: 输入:4 3 输出:6划分方案数\(i.e.\)第二类斯特林数,其实也就是第二类斯特林数的定义啦~ 3.卡特兰数(Catalan)重头戏来了,或者说正片开始 前几项为(从第0项开始):1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ... 首先卡特兰数的递推式就有4个: 两个递推公式: 递推式一: \[h[n]=\sum_{i = 0}^nh[i]\times h[n-1] = h[0]\times h[n−1]+...+h[n−i]\times h[0](n\in N^*;n≥2) \]递推式二: \[h[n+1]=\frac{2(2n-1)}{n+2}\times h[n](n\in N^*;n\geq 2) \]其中:$$h[1]=h[0]=0$$ 两个组合数公式或者说通项公式: 组合公式一: \[h(n)=\frac{1}{(n+1)}\sum_{i = 0}^{n}(C_n^i)^2 (n\in N) \]组合公式二: \[h(n)=\frac{1}{n+1}C^n_{2n}=C_{2n}^{n} - C_{2n}^{n-1} (n\in N) \]情景一、n个元素序列的进出栈方案数(h(n))一个进栈序列n,有多少个不同的出栈序列?P1044 [NOIP2003 普及组] 栈 比如序列1 2 3 4,共有1 2 3 4,1 2 4 3,1 3 2 4,1 3 4 2,1 4 3 2
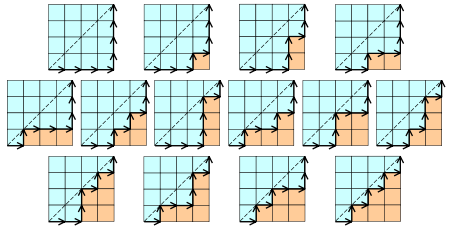
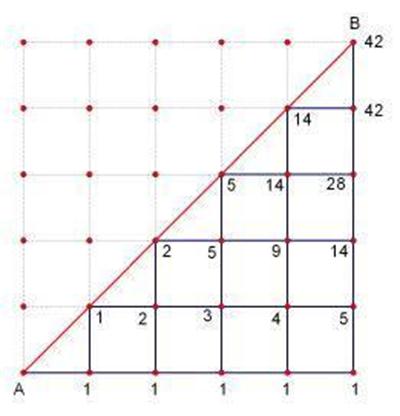
从原点(0,0)出发,每次向x轴或者y轴正方向移动1个单位,直到到达(n,n)点,且在移动过程中不越过第一象限平分线的移动方案总数。 在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?其实向右走相当于进栈,向左走相当于出栈,本质就是n个数出栈次序的问题,所以答案就是卡特兰数。
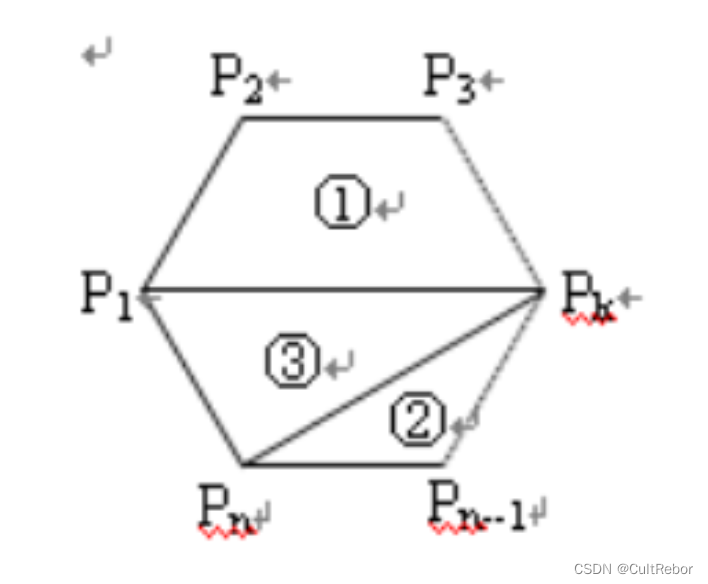
一个凸的n边形,用直线连接其中两个顶点使之分成多个三角形,每条直线不能相交,问一共有多少种划分方案。 我们不妨任取三个点\(P_1、P_k、P_n\),以这三个点为基准三角形。 区域①是一个凸\(k\)边形,区域②是一个凸\(n-k+1\)边形, 区域①的拆分方案总数是\(f(k)\); 区域②的拆分方案数为\(f(n-k+1)\); 故包含\(△P_1P_kP_n\)的\(n\)边形的拆分方案数为\(f(k)* f(n-k+1)\)种 那么总方案数就是 \[F(n)=\sum_{i=2}^{n-1}f(i)\times f(n-i+1) \]而将一个凸\(n+2\)边形区域分成三角形区域的方法数就是卡特兰数 情景四、n节点能构成的二叉树的个数(h(n))n个节点所能构成的满二叉树的个数也符合卡特兰数。 向左记为+1,向右记为−1,按照向左优先的原则,从根节点开始遍历。例如第一个图记为\(+1,+1,+1,−1,−1,−1\)。这种形式的遍历都符合卡特兰数的规则。 或者可以这样考虑根肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式,\(T(0, n-1),T(1, n-2),...,T(n-1, 0)\),设\(T(i, j)\)表示根的左子树含i个结点,右子树含j个结点。 设问题的解为\(f(n)\),那么\(f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)\)。 卡特兰推导公式呗。
当前有n对括号,请问有多少种合法的排列方式。 比如n=3时,所有合法的括号表达式有 ((())), (())(), ()(()), ()()(), (()()), 共5个。 \(n\)对括号相当于有\(2n\)个符号,\(n\)个左括号、\(n\)个右括号,可以设问题的解为\(f(2n)\)。 \(f(2n)\)可以转化如下的递推式 \(f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)\)。 再不会要打屁股了 情景六、 n个数连乘括号化的方案数\((h(n-1))\)\(P=A_1\times A_2\times A_3\times A_4\times …\times A_n\) 可以通过乘法结合律给这个式子由繁而简地括号化。分成\((A_1)×(A_2×A_3.....A_n)\),然后再对\((A_1)\)和\((A_2×A_3.....A_n)\)分别括号化。分成\((A_1×A_2)×(A_3.....A_n)\),然后再对\((A_1×A_2)\)和\((A_3.....A_n)\)括号化 $ f(n) = f(1)f(n-1) + f(2)f(n-2) + f(3)f(n-3) + f(n-1)f(1)\(。\)f(1)*f(n-1)\(表示分成\)(A_1)×(A_2×A_3.....A_n)$两部分,然后分别括号化。 情景七、在圆上选择\(2n\)个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数\((h(n))\)以其中一个点为基点,设其编号为\(0\),然后按顺时针方向将其他点依次编号。那么与编号为\(0\)相连点的编号一定是奇数,否则,这两个编号间含有奇数个点,势必会有个点被孤立,即在一条线段的两侧分别有一个孤立点,从而导致两线段相交。 设选中的基点为\(A\),与它连接的点为\(B\),那么\(A\)和\(B\)将所有点分成两个部分,再对这两部分求解即可。 设问题的解\(f(n)\),那么\(f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ...+f(n-4)*f(2) + f(n-2)*f(0)\)。熟悉的配方。 情景八、n个长方形填充一个高度为n的阶梯状图形的方法个数?卡特兰数,不推了。
送一道真题作为送别 【NOIP2018提高组初赛第八题】关于 \(Catalan\) 数 \(C_n = \frac{(2n)!}{(n + 1)!n !}\),下列说法中错误的是( \(A\) )。 \(A\). \(C_n\) 表示有 \(n + 1\) 个结点的不同形态的二叉树的个数。 \(B\). \(C_n\) 表示含 \(n\) 对括号的合法括号序列的个数。 \(C\). \(C_n\) 表示长度为 \(n\) 的入栈序列对应的合法出栈序列个数。 \(D\). \(C_n\) 表示通过连接顶点而将 \(n +2\) 边的凸多边形分成三角形的方法个数。 解析:只要往上翻一下,发现\(A\)中其实应该是是\(n\)个节点。 结束参考: https://www.luogu.com.cn/problem/P1720 https://www.luogu.com.cn/problem/solution/P8143 https://www.cnblogs.com/owenyu/p/6724661.html https://www.luogu.com.cn/problem/solution/P1044 https://baike.baidu.com/item/斯特林数/4938529?fr=aladdin https://blog.csdn.net/chenlong_cxy/article/details/113613203 http://t.zoukankan.com/Staceyacm-p-10781754.html https://blog.csdn.net/doc_sgl/article/details/8880468?spm=1001.2101.3001.6650.10&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-10-8880468-blog-88906534.pc_relevant_multi_platform_featuressortv2dupreplace&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-10-8880468-blog-88906534.pc_relevant_multi_platform_featuressortv2dupreplace&utm_relevant_index=16 https://ti.luogu.com.cn/problemset/1029 |
【本文地址】