焦半径公式及其应用

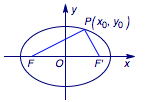
本文研究如何从圆锥曲线（特指椭圆、双曲线、抛物线）的定义与标准方程出发，去推导与焦点相关的焦半径公式、焦点弦长公式及其相关的结论与应用．

为了方便起见，本文中不作特别说明，椭圆、双曲线、抛物线都是针对焦点在$x$轴上标准方程（其中抛物线考虑标准方程$y^2=2px,p>0$），$F(-c,0),F'(c,0)$分别为椭圆或双曲线的左、右焦点，$F\left(\dfrac p2,0\right )$是抛物线的焦点，$P(x_0,y_0)$是相应圆锥曲线上的一点．另外，所有的公式推导均以椭圆方程为例，且优先考虑左焦点对应的相关公式．双曲线可以完全类比椭圆的推导过程得到，特殊情况会另外说明．

焦半径是指圆锥曲线上任意一点与焦点的连线段．对于椭圆与双曲线上的任意一点，都对应两条焦半径；对于抛物线上的任意一点，焦半径唯一存在．

设$P(x_0,y_0)$是椭圆上任意一点，则有$$\dfrac{x_{0}^2}{a^2}+\dfrac{y_{0}^2}{b^2}=1,$$从而焦半径\[\begin{split} |PF|&=\sqrt{(x_0+c)^2+y_0^2}\\&=\sqrt{(x_0+c)^2+b^2\left(1-\dfrac{x_0^2}{a^2}\right)}\\&=\left |a+\dfrac{c}{a}x_0\right |.\end{split} \]而$x_{0}\in[-a,a]$，所以$$|PF|=a+ex_{0},$$其中$e$为椭圆的离心率．

事实上，在由椭圆的定义推导椭圆方程的过程中，就已经产生了这个式子，设$M(x,y)$满足$$|MF_{1}|+|MF_{2}|=2a,$$即\[\begin{eqnarray} \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a,\end{eqnarray} \]分子有理化得\[\dfrac{4cx}{\sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}}=2a,\]于是有\[\begin{eqnarray} \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=\dfrac{2cx}{a}.\end{eqnarray} \] (1)(2)两式相加得$$\sqrt{(x+c)^{2}+y^{2}}=a+\dfrac cax=a+ex,$$即为椭圆上一点$M(x,y)$到椭圆左焦点的距离．

于是我们得到椭圆的焦半径公式（I）：$$|PF|=a+ex_{0},|PF'|=a-ex_{0}.$$同理有双曲线的焦半径公式（I）：$$|PF|=|a+ex_0|,|PF'|=|a-ex_0|.$$当点在双曲线上的不同支上时，绝对值里面式子的正负大家可以自行讨论．

抛物线的焦半径公式可以直接由抛物线的定义得到，即$$|PF|=x_0+\dfrac p2.$$

例1　椭圆$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1(a>b>0)$的右焦点为$F$，直线$x=\dfrac {a^2}{c}$与$x$轴的交点为$A$，在椭圆上存在点$P$满足线段$AP$的垂直平分线过点$F$，则椭圆离心率的取值范围是____．

正确答案是$\left[\dfrac 12,1\right )$．

解　设$P(x_0,y_0)$，则有$|PF|=|FA|$，即$$a-ex_0=\dfrac {a^2}{c}-c,$$解得$$x_0=\dfrac {a^2}{c}+a-\dfrac {a^3}{c^2}.$$又因为$x_0\in [-a,a]$，所以有$$-a\leqslant \dfrac {a^2}{c}+a-\dfrac {a^3}{c^2}\leqslant a,$$两边同除$a$可解得$$\dfrac 12\leqslant e