| 线代:1.2矩阵的行列式 | 您所在的位置:网站首页 › 三行三列乘以一行三列矩阵 › 线代:1.2矩阵的行列式 |
线代:1.2矩阵的行列式
|
文章目录
任务详解:1.行列式的引入二阶行列式三阶行列式计算三阶或更加高阶的行列式
2.行列式的计算与重要性质3.行列式按行(列)展开,代数余子式4.克莱姆法则
本课程来自深度之眼,部分截图来自课程视频。 【第一章 线性代数】1.2矩阵的行列式 在线LaTeX公式编辑器 任务详解:这节课主要介绍了行列式的引入,行列式的计算与重要性质,行列式按行(列)展开,代数余子式,克莱姆法则,矩阵的逆,矩阵逆的性质等知识点。 掌握目标: 1、了解如何从解方程的角度引入二阶三阶行列式 2、掌握全排列,逆序数,以及n阶方阵行列式的一般运算公式 3、掌握特殊矩阵:对角矩阵,上(下)三角矩阵行列式的公式 4、熟练掌握行列式的性质,以及如何通过变换转为上(下)三角矩阵来简化行列式的计算 5、掌握行列式的按行按列展开,余子式和代数余子式 6、了解克莱姆法则,掌握n*n方程组的解的个数的定理 1.行列式的引入 二阶行列式行列式最早是从解方程组的角度来的,例如二阶行列式: 用消元法解二元线性方程组: { a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases}a_{11}x_{1}+a_{12}x_{2}=b_{1}\\\\a_{21}x_{1}+a_{22}x_{2}=b_{2}\end{cases} ⎩⎪⎨⎪⎧a11x1+a12x2=b1a21x1+a22x2=b2 为消去未知数 x 2 x_2 x2,以 a 22 a_{22} a22与 a 12 a_{12} a12分别乘上列两方程的两端,然后两个方程相减,得: ( a 11 a 22 − a 12 a 21 ) x 1 = b 1 a 22 − a 12 b 2 (a_{11}a_{22}-a_{12}a_{21})x_{1}=b_{1}a_{22}-a_{12}b_{2} (a11a22−a12a21)x1=b1a22−a12b2 消去未知数
x
1
x_1
x1得:
(
a
11
a
22
−
a
12
a
21
)
x
2
=
a
11
b
2
−
b
1
a
21
(a_{11}a_{22}-a_{12}a_{21})x_{2}=a_{11}b_{2}-b_{1}a_{21}
(a11a22−a12a21)x2=a11b2−b1a21 求得方程组的解为
x
1
=
b
1
a
22
−
a
12
b
2
a
11
a
22
−
a
12
a
21
x_{1}=\frac{b_{1}a_{22}-a_{12}b_{2}}{a_{11}a_{22}-a_{12}a_{21}}
x1=a11a22−a12a21b1a22−a12b2
x
2
=
a
11
b
2
−
b
1
a
21
a
11
a
22
−
a
12
a
21
x_{2}=\frac{a_{11}b_{2}-b_{1}a_{21}}{a_{11}a_{22}-a_{12}a_{21}}
x2=a11a22−a12a21a11b2−b1a21 公式输入好累,还是截图方便。 若记(D) 下面称为3* 3数表的三阶行列式。按照此式的定义,三元一次方程组也是满足前面二元一次方程组的行列式表达形式,后面更加通用的克莱姆法则。 1.全排列:比如1,2,3的全排列有哪些。 123/132/213/231/312/321, 也就是n个数的全排列有n!种 2.逆序数:记为t,直接看例子 求排列32514的逆序数. 解在排列32514中: 3排在首位,逆序数为0; 2的前面比2大的数有一个(3),故逆序数为1; 5是最大数,逆序数为0; 1的前面比1大的数有三个(3、2、5),故逆序数为3; 4的前面比4大的数有一个(5),故逆序数为1; 于是这个排列的逆序数为t=0+1+0+3+1=5. 下面来计算三阶行列式: 性质1:行列式与它的转置行列式相等:
∣
A
T
∣
=
∣
A
∣
|A^T|=|A|
∣AT∣=∣A∣ 性质2:互换行列式的两行(列),行列式变号 以上两个性质要很熟悉! 推论:如果行列式有两行(列)完全相同,则此行列式等于零. 性质3:行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘此行列式. 性质4:行列式中如果有两行(列)元素成比例,则此行列式等于零. 性质5:若行列式的某一列(行)的元素都是两数之和,例如第i列的元素都是两数之和: 降阶处理,用低阶的行列式来算高阶的行列式 先导概念:余子式,代数余子式 克莱姆法则如下图所示,注意两点: 1、D(系数行列式不能为0); 2、
D
j
D_j
Dj是把常数项
b
b
b替换第j列得到的行列式。 |
【本文地址】
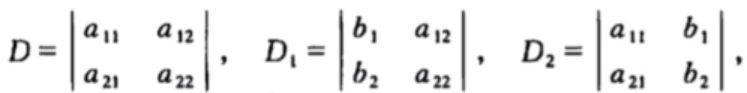 则方程组的解可以写为
则方程组的解可以写为 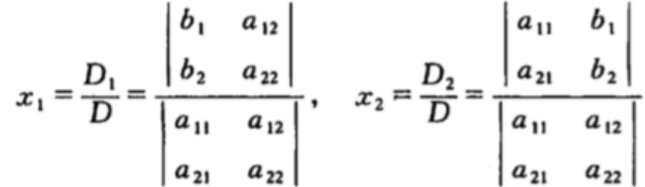 以上就是引入行列式的内容,那行列式和矩阵什么关系? 如果矩阵记为A,则行列式记为|A|,行列式的值是一个实数,例如: 设有9个数排成3行3列的数表
以上就是引入行列式的内容,那行列式和矩阵什么关系? 如果矩阵记为A,则行列式记为|A|,行列式的值是一个实数,例如: 设有9个数排成3行3列的数表  记为:
记为: 
 注意: 我们已经学过矩阵,所以这里的数表我们就认为是一个3*3的矩阵,对应的行列式称为矩阵的行列式
注意: 我们已经学过矩阵,所以这里的数表我们就认为是一个3*3的矩阵,对应的行列式称为矩阵的行列式 可以看到,总共有六项,每项的
a
i
j
a_{ij}
aij的第一个系数i都是1.2.3 每项
a
i
j
a_{ij}
aij的第二个系数j是123这三个数字的全排列,各个全排列的逆序数t为: 123(t=0) 231(t=2) 312(t=2) —kawayiの分割线—上偶下奇 132(t=1) 213(t=1) 321(t=3) 可以看到逆序数为偶数的为正,奇数为负。所以可以写成:
可以看到,总共有六项,每项的
a
i
j
a_{ij}
aij的第一个系数i都是1.2.3 每项
a
i
j
a_{ij}
aij的第二个系数j是123这三个数字的全排列,各个全排列的逆序数t为: 123(t=0) 231(t=2) 312(t=2) —kawayiの分割线—上偶下奇 132(t=1) 213(t=1) 321(t=3) 可以看到逆序数为偶数的为正,奇数为负。所以可以写成: 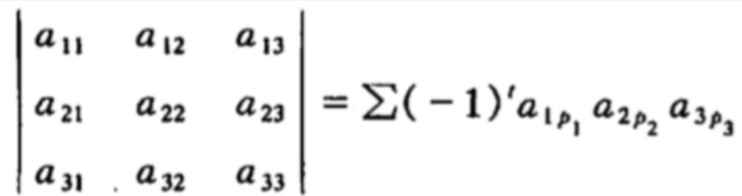 对于n阶行列式:
对于n阶行列式:  推论:对于对角矩阵(主对角矩阵)有
推论:对于对角矩阵(主对角矩阵)有  副对角矩阵有:
副对角矩阵有: 
 性质6:把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.
性质6:把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.  上式可以根据性质4分两项,第一项和原来的行列式一样,第二项因为后面加上那个部分是成比例,根据性质4为0. 下面是一个行列式计算的例子,总体的思想是把三角区域变成0,最后的行列式的值等于对角线的元素的乘积。其中c是column,r是row。为了避免分数,要计算的元素最好是1.例如刚开始的时候把第二列和第一列互换位置
上式可以根据性质4分两项,第一项和原来的行列式一样,第二项因为后面加上那个部分是成比例,根据性质4为0. 下面是一个行列式计算的例子,总体的思想是把三角区域变成0,最后的行列式的值等于对角线的元素的乘积。其中c是column,r是row。为了避免分数,要计算的元素最好是1.例如刚开始的时候把第二列和第一列互换位置 
 引理一个n阶行列式,如果其中第i行所有元素除(i,j)元
a
i
j
a_{ij}
aij外都为零,那么这行列式等于
a
i
j
a_{ij}
aij与它的代数余子式的乘积,即
D
=
a
i
j
A
i
j
D=a_{ij}A_{ij}
D=aijAij 这个引理的证明过程大概思路如下: 第一步,先可以证明这个: 如果有一个行列式,可以分为四块,其中一块为0
引理一个n阶行列式,如果其中第i行所有元素除(i,j)元
a
i
j
a_{ij}
aij外都为零,那么这行列式等于
a
i
j
a_{ij}
aij与它的代数余子式的乘积,即
D
=
a
i
j
A
i
j
D=a_{ij}A_{ij}
D=aijAij 这个引理的证明过程大概思路如下: 第一步,先可以证明这个: 如果有一个行列式,可以分为四块,其中一块为0  记左上和右下为:
记左上和右下为:  则有:
D
=
D
1
D
2
D=D_1D_2
D=D1D2 第二步,根据上面的推论,先证(i,j)=(1,1)的情形,此时
则有:
D
=
D
1
D
2
D=D_1D_2
D=D1D2 第二步,根据上面的推论,先证(i,j)=(1,1)的情形,此时  这个好证,可以把推论中的
D
1
D_1
D1看做是
a
11
a_{11}
a11,其他的
这个好证,可以把推论中的
D
1
D_1
D1看做是
a
11
a_{11}
a11,其他的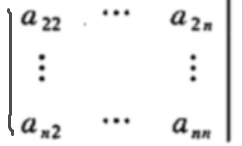 看做是
D
2
D_2
D2 根据推论的结果就可以得到
D
=
a
i
j
A
i
j
D=a_{ij}A_{ij}
D=aijAij 第三步,再证明
a
i
j
a_{ij}
aij在任意位置的情况:
看做是
D
2
D_2
D2 根据推论的结果就可以得到
D
=
a
i
j
A
i
j
D=a_{ij}A_{ij}
D=aijAij 第三步,再证明
a
i
j
a_{ij}
aij在任意位置的情况:  这个时候,把
a
i
j
a_{ij}
aij所在的行和列进行交换,是的
a
i
j
a_{ij}
aij变到
a
11
a_{11}
a11位置(每交换一次就要乘一次-1),再利用第二步的结果就可以得证。原文描述如下:
这个时候,把
a
i
j
a_{ij}
aij所在的行和列进行交换,是的
a
i
j
a_{ij}
aij变到
a
11
a_{11}
a11位置(每交换一次就要乘一次-1),再利用第二步的结果就可以得证。原文描述如下:  上面啰嗦这么多,主要是为了这个定理3:行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即
上面啰嗦这么多,主要是为了这个定理3:行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即 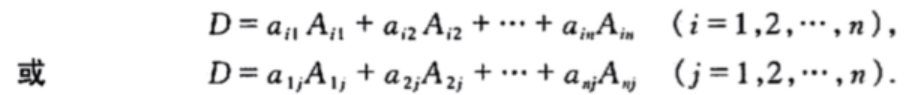 这个东西的证明要用到行列式的性质5.然后把下面式子拆分为n项
这个东西的证明要用到行列式的性质5.然后把下面式子拆分为n项  接下来拆分
接下来拆分  上面的第一项可以写为
a
i
1
A
i
1
a_{i1}A_{i1}
ai1Ai1,第二项为
a
i
2
A
i
2
a_{i2}A_{i2}
ai2Ai2,…第n项为
a
i
n
A
i
n
a_{in}A_{in}
ainAin。也就是定理得证。 推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.即
上面的第一项可以写为
a
i
1
A
i
1
a_{i1}A_{i1}
ai1Ai1,第二项为
a
i
2
A
i
2
a_{i2}A_{i2}
ai2Ai2,…第n项为
a
i
n
A
i
n
a_{in}A_{in}
ainAin。也就是定理得证。 推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.即 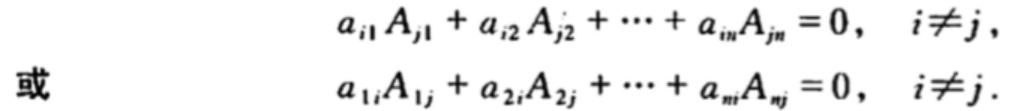 证明过程思想是这样,如果一个正常的行列式要展开,按定理三有:
证明过程思想是这样,如果一个正常的行列式要展开,按定理三有:  这个等式左边和推论中的东西不一样,如果我们把行列式中的第j行替换为第i行,变成:
这个等式左边和推论中的东西不一样,如果我们把行列式中的第j行替换为第i行,变成:  也就是上面等式中的左边的
a
j
1
a_{j1}
aj1换成了
a
i
1
a_{i1}
ai1,
a
j
2
a_{j2}
aj2换成了
a
i
2
a_{i2}
ai2,…,
a
j
n
a_{jn}
ajn换成了
a
i
n
a_{in}
ain,所以等式左边变成了:
也就是上面等式中的左边的
a
j
1
a_{j1}
aj1换成了
a
i
1
a_{i1}
ai1,
a
j
2
a_{j2}
aj2换成了
a
i
2
a_{i2}
ai2,…,
a
j
n
a_{jn}
ajn换成了
a
i
n
a_{in}
ain,所以等式左边变成了: 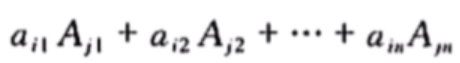 也就是推论的左边形式出来了。 这个时候观察第j行替换为第i行后的行列式,根据行列式的推论可知,该行列式为0,本推论都证。 以上三节都是讲行列式的基础知识,下面是行列式的一个重要法则,以及矩阵的逆方面的知识点
也就是推论的左边形式出来了。 这个时候观察第j行替换为第i行后的行列式,根据行列式的推论可知,该行列式为0,本推论都证。 以上三节都是讲行列式的基础知识,下面是行列式的一个重要法则,以及矩阵的逆方面的知识点
 定理4:如果线性方程组(11)的系数行列式D≠0,则(11)一定有解,且解是惟一的. 定理4的逆否定理为: 定理4’:如果线性方程组(11)无解或有两个不同的解,则它的系数行列式必为零。 对于齐次线性方程组
定理4:如果线性方程组(11)的系数行列式D≠0,则(11)一定有解,且解是惟一的. 定理4的逆否定理为: 定理4’:如果线性方程组(11)无解或有两个不同的解,则它的系数行列式必为零。 对于齐次线性方程组  PS:齐次线性方程组的解一定是有x1~ n都等于0. 定理5:如果齐次线性方程组(13)的系数行列式D≠0,则齐次线性方程组(13)没有非零解. 定理5’:如果齐次线性方程组(13)有非零解,则它的系数行列式必为零
PS:齐次线性方程组的解一定是有x1~ n都等于0. 定理5:如果齐次线性方程组(13)的系数行列式D≠0,则齐次线性方程组(13)没有非零解. 定理5’:如果齐次线性方程组(13)有非零解,则它的系数行列式必为零