Metropolis

假设我们有一个矩形区域\(R\)，面积为\(S_0\)。在此区域中，有一个不规则区域\(M\)，其面积\(S\)待求。

方法1：把不规则区域\(M\)划分为多个小的规则区域，由这些规则区域的面积总和\(S'\)近似。

方法2：抓一把黄豆，均匀铺在\(R\)中，再统计落在不规则区域\(M\)中的黄豆比例。该比例可近似\(\frac{S}{S_0}\)。 方法2采用的是抽样（采样）解决问题的思想，即随机模拟。

因此，随机模拟的关键，在于如何将实际复杂问题，转化为抽样可以解决的问题。当然，这非常灵活，也考验我们的创造力。

我们接下来的核心问题，是利用计算机可直接实现的均匀抽样，借助随机模拟的方法，实现满足特定概率分布\(p(x)\)的抽样。

当我们的概率分布很简单时，如\([0,1]\)上的均匀分布，抽样是很好实现的。现成的随机算法非常多。

但是，对于其他更复杂的分布，如果我们还想借助简单的均匀随机抽样，就需要换换思路了。

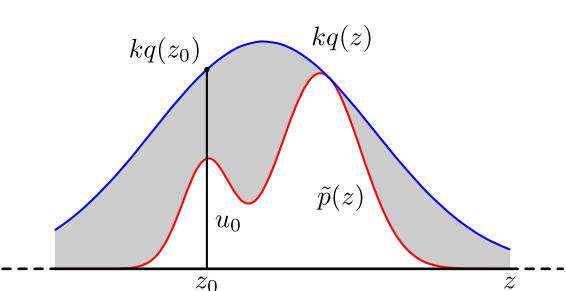
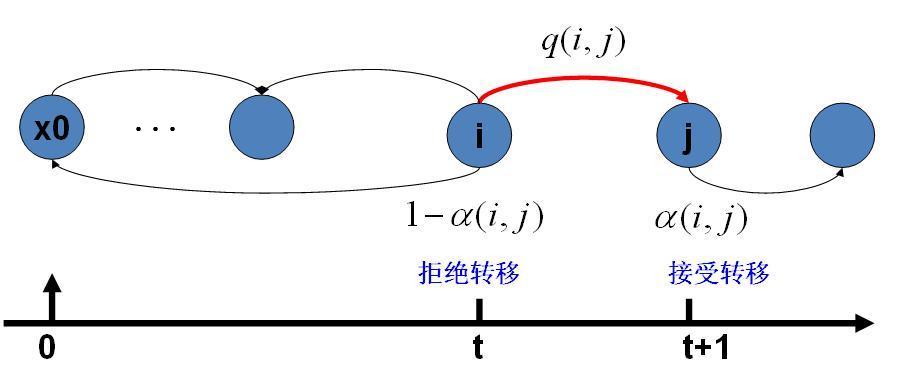
例如上图中的\(p(z)\)（忽略波浪号），是较为复杂的概率密度函数。

我们先构造比较简单的、容易抽样的高斯分布\(q(z)\)，乘一个常数\(k\)，使之满足：

拒绝抽样的方法是：

对高斯分布的样本进行采样，得到一个\(z_0\)，如图；

在\([0,kq(z_0)]\)上均匀采样，得到\(u_0\)；

如果\(u_0 > p(z)\)，就拒绝该采样结果；反之接受；

重复直到接受足够多的样本。

我们理解一下为什么拒绝抽样是可行的，这对我们之后运用随机模拟思想非常关键！

该简单分布与高斯分布的趋势大致相同，中间大两头小，因此取到中间的\(z\)的概率比较大；

通过\(u_0\)进一步筛选\(z\)，\(p(z)\)较低时拒绝率较大，反之接受率较高，大致符合\(p(z)\)分布要求。

一句话，通过简单抽样和设置接受率，“强迫”结果趋于复杂分布。

这样，我们就通过简单的高斯分布采样，以及计算机可直接实现的均匀采样，间接实现了复杂的\(p(z)\)采样。

然而，在高维情况下，该方法的劣势很明显：

合适的简单分布\(q(z)\)很难找到。

合适的\(k\)值很难找到。

这两个问题会导致拒绝率极高，计算效率很低。其根本缺陷在于：样本之间是独立无关的。

结合马氏链知识（参考信息论相关书籍），我们知道： 对于遍历的马尔可夫链，当其转移次数足够多时，将会进入稳态分布\(\pi (x)\)，即各状态的出现概率趋于稳定。

进一步，假设变量\(\boldsymbol X\)所有可能的取值，构成某遍历马氏链的状态空间。 则无论从什么状态出发，只要转移步数足够大，该马氏链将趋于稳定，即逐渐开始依次输出符合\(p(x)\)分布的状态\(X_i\)。 这样，通过收集马氏链收敛后产生的\(X_i\)，我们就得到了符合分布\(p(x)\)的样本。 此时稳态分布即\(\pi (x)=p(x)\)。

比如，我们希望抽样样本满足指数分布。此时，整数0到正无穷都是状态，但整数0的出现概率最大，随着数增大，出现概率越来越小。我们构造一个稳定输出服从指数分布状态的马氏链，则得到的样本服从指数分布。

这个绝妙的想法在1953年由Metropolis提出。为了研究粒子系统的平稳性质，Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法（Metropolis算法），并在最早的计算机上编程实现。

Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法，所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中， Metropolis算法也被选为二十世纪的十个最重要的算法之一。

我们接下来介绍的MH算法是Metropolis 算法的一个常用的改进变种。 由于马氏链的收敛性质主要由转移矩阵\(\boldsymbol P\)决定, 所以基于马氏链做采样的关键问题是：如何构造转移矩阵\(\boldsymbol P\)，使平稳分布恰好是我们要的分布\(p(x)\)。

定理——细致平稳条件：

若非周期马氏链的转移矩阵\(\boldsymbol P\)和分布\(\pi (x)\)满足：

则分布\(\pi (x)\)是马氏链的平稳分布。

证明：

这说明：

因此\(\pi (x)\)是平稳分布。

物理意义：

对于任意两个状态\(i,j\)，从状态\(i\)流失到状态\(j\)的概率质量，等于反向流动的概率质量，因此是状态概率是稳定的。

假设我们已经有了一个转移矩阵\(\boldsymbol Q\)。一般情况下，该转移矩阵不满足细致平稳条件：

我们引入接受率\(\alpha(i,j)\)，满足：

其中：

\(P(i)\)是状态\(i\)出现的概率，是假设马氏链满足复杂分布时输出状态的概率。

\(\boldsymbol Q\)是初始转移概率矩阵，满足任意一个给定的简单分布，便于抽样即可。

显然，接受率最简单的构造方法是：

此时，细致平稳条件成立，该马氏链输出的状态满足稳态分布\(p(x)\)！

综上，有几个要点必须要理解，有助于我们编程实现：

我们引入接受率，使得该马氏链以转移概率\(\boldsymbol Q_{ij}\alpha(i,j)\)从状态\(i\)转移到状态\(j\)。

该转移概率的实现方式是：我们先按\(\boldsymbol Q_{ij}\)生成新状态，再按\(\alpha(i,j)\)的概率接受转移结果，乘积即为\(\boldsymbol Q_{ij}\alpha(i,j)\)转移概率。

一定要理解这个接受率！在拒绝抽样中，如果\(u_0 > p(z)\)，我们会放弃抽样结果，不纳入最终的统计。正是因为如此，抽样才会逼近复杂分布。而这里的接受是“接受转移”，如果\(u>\alpha\)，意味着\(t+1\)时刻状态和\(t\)时刻相同，并且应该纳入统计而不是放弃结果！！

由于状态出现概率和转移概率满足细致平稳条件，因此状态出现概率即稳态分布概率。长期转移后，我们会得到想要的抽样分布效果。

图解转移过程：

要注意的是，当马氏链处在状态\(i\)时，我们并不知道如何选择下一个状态\(j\)。 我们在这里采用抽样的方法，并借助接受率，“强迫”转移过程逼近理想的遍历马氏链转移过程。

算法描述如下：

初始化马氏链状态\(X_0=x_0\)

从\(t=0\)开始，重复以下步骤：

假设该\(t\)时刻状态为\(X_t=x_t\)；

对\(Q_{x_t,x}\)抽样，随机得到一个状态\(x_{next}\)；

在\([0,1]\)上均匀抽样，得到一个\(u\)；

若\(u