（四）【矩阵论】（线性变换）线性变换的定义

【矩阵论专栏】

（1）定义1（线性变换）设 V ! ， V 2 V_!，V_2 V!​，V2​是同一数域 F F F上的线性空间， T T T是 V 1 → V 2 V_1\rightarrow V_2 V1​→V2​的映射，若对 V 1 V_1 V1​中任意向量 α ， β \alpha，\beta α，β，以及数域 F F F中任意元素 k k k，有： T ( α + β ) = T α + T β T(\alpha+\beta)=T\alpha+T\beta T(α+β)=Tα+Tβ T ( k α = k T α ) T(k\alpha=kT\alpha) T(kα=kTα) 则称 T T T为线性空间 V 1 V_1 V1​到 V 2 V_2 V2​的线性变换（或线性算子）。

例1： 例2：

例3：

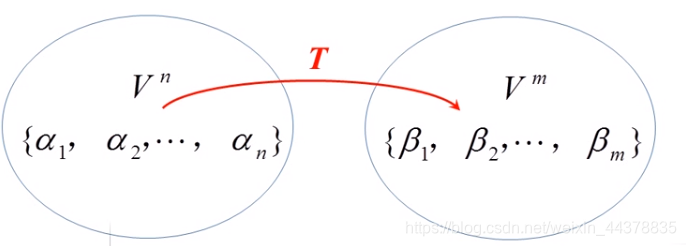
设 T T T是 V n → V m V^n\rightarrow V^m Vn→Vm的线性变换， B α = { α 1 , α 2 , . . . , α n } \Beta_\alpha=\{\alpha_1,\alpha_2,...,\alpha_n\} Bα​={α1​,α2​,...,αn​}与 B β = { β 1 , β 2 , . . . , β m } \Beta_\beta=\{\beta_1,\beta_2,...,\beta_m\} Bβ​={β1​,β2​,...,βm​}分别是 V n V^n Vn与 V m V^m Vm的基。 因为 T α i ∈ V m , i = 1 , 2 , . . , n . T\alpha_i\in V^m,i=1,2,..,n. Tαi​∈Vm,i=1,2,..,n.设 T α i T\alpha_i Tαi​在基 B β = { β 1 , β 2 , . . . , β m } \Beta_\beta=\{\beta_1,\beta_2,...,\beta_m\} Bβ​={β1​,β2​,...,βm​}下的坐标为： A i = [ a 1 i . . a m i ] , i = 1 , 2 , . . . , n . A_i=\begin{bmatrix}a_{1i}\\.\\.\\a_{mi}\end{bmatrix},i=1,2,...,n. Ai​=⎣⎢⎢⎡​a1i​..ami​​⎦⎥⎥⎤​,i=1,2,...,n.即有 T α i = B β A i T\alpha_i=\Beta_\beta A_i Tαi​=Bβ​Ai​，i=1,2,…,n.

记 T B α = { T α 1 , T α 2 , . . . , T α n } T\Beta_{\alpha}=\{T\alpha_1,T\alpha_2,...,T\alpha_n\} TBα​={Tα1​,Tα2​,...,Tαn​}

则有： T B α = { T α 1 , T α 2 , . . . , T α n } = { B β A 1 , B β A 2 , . . . , B β A n } = B β { A 1 , A 2 , . . . , A n } = B β A T\Beta_\alpha=\{T\alpha_1,T\alpha_2,...,T\alpha_n\}=\{\Beta_\beta A_1,\Beta_\beta A_2,...,\Beta_\beta A_n\}=\Beta_\beta\{A_1,A_2,...,A_n\}=\Beta_\beta A TBα​={Tα1​,Tα2​,...,Tαn​}={Bβ​A1​,Bβ​A2​,...,Bβ​An​}=Bβ​{A1​,A2​,...,An​}=Bβ​A

其中 A = [ A 1 , A 2 , . . . , A n ] A=[A_1,A_2,...,A_n] A=[A1​,A2​,...,An​]

A A A：每一列对应的都是 B α 里 的 向 量 α i 做 完 线 性 变 换 T 后 ， T α i 在 基 B β 下 的 坐 标 \Beta_\alpha里的向量\alpha_i做完线性变换T后，T\alpha_i在基\Beta_\beta 下的坐标 Bα​里的向量αi​做完线性变换T后，Tαi​在基Bβ​下的坐标

定义2 称矩阵 A A A为线性变换 T T T在基偶 { B α ， B β } \{\Beta_{\alpha}，\Beta_{\beta}\} {Bα​，Bβ​}下的矩阵。若 T T T是 V n → V n V^n\rightarrow V^n Vn→Vn（自身）的线性变换，则取 B β = B α \Beta_{\beta}=\Beta_{\alpha} Bβ​=Bα​，此时 A A A是方阵，简称为 T T T在基 B α \Beta_{\alpha} Bα​下的矩阵。 A = [ A 1 ， A 2 ， . . . ， A n ] A=[A_1，A_2，...，A_n] A=[A1​，A2​，...，An​] 其中 A i A_i Ai​是 T α i T\alpha_i Tαi​在像空间 B β \Beta_{\beta} Bβ​下的坐标。

基到基的过渡矩阵P与线性变换在基偶下的矩阵A的联系：

例子：

2)中的 [ 1 , 0 , 0 ] T [1 ,0, 0]^T [1,0,0]T：取A第一列

（1）定义3（零空间和值空间）设 T T T是 V n → V m V^n\rightarrow V^m Vn→Vm的线性变换，记 N ( T ) = { ξ ∈ V n ∣ T ξ = 0 } N(T)=\{\xi\in V^n|T\xi=0\} N(T)={ξ∈Vn∣Tξ=0} R ( T ) = { T ξ ∈ V m ∣ ξ ∈ V n } R(T)=\{T\xi\in V^m|\xi\in V^n\} R(T)={Tξ∈Vm∣ξ∈Vn}称 N ( T ) N(T) N(T)为T的零空间（核） 称 R ( T ) R(T) R(T)为T的值空间（值域） 易知， N ( T ) N(T) N(T)是 V n V^n Vn的子空间； R ( T ) R(T) R(T)是 V m V^m Vm的子空间。

（2）定义4（零度与秩）设 T T T是 V n → V m V^n\rightarrow V^m Vn→Vm的线性变换，记 n u l l ( T ) = d i m N ( T ) null(T)=dimN(T) null(T)=dimN(T) r a n k ( T ) = d i m R ( T ) rank(T)=dimR(T) rank(T)=dimR(T)称 n u l l ( T ) 为 null(T)为 null(T)为 T T T的零度, 称 r a n k ( T ) rank(T) rank(T)为 T T T的秩。

（3）定理1设 T T T是 V n → V m V^n\rightarrow V^m Vn→Vm的线性变换， B α = { α 1 , α 2 , . . . , α n } \Beta_\alpha=\{\alpha_1,\alpha_2,...,\alpha_n\} Bα​={α1​,α2​,...,αn​}与 B β = { β 1 , β 2 , . . . , β m } \Beta_\beta=\{\beta_1,\beta_2,...,\beta_m\} Bβ​={β1​,β2​,...,βm​}分别是 V n V^n Vn与 V m V^m Vm的基， T T T在基偶 { B α , B β } \{\Beta_\alpha,\Beta_\beta \} {Bα​,Bβ​}下的矩阵为 A A A，则有： 1 ) n u l l ( T ) = d i N ( A ) = n − r a n k ( A ) 1)null(T)=diN(A)=n-rank(A) 1)null(T)=diN(A)=n−rank(A) 2 ) r a n k ( T ) = d i m R ( A ) = r a n k ( A ) 2)rank(T)=dimR(A)=rank(A) 2)rank(T)=dimR(A)=rank(A) 3 ) r a n k ( T ) + n u l l ( T ) = n 3)rank(T)+null(T)=n 3)rank(T)+null(T)=n

例题：

（4）求零空间 N ( T ) N(T) N(T)与值空间 R ( T ) R(T) R(T)的基的一般方法：

设 T T T是 V n → V m V^n\rightarrow V^m Vn→Vm的线性变换， B α = { α 1 , α 2 , . . . , α n } \Beta_\alpha=\{\alpha_1,\alpha_2,...,\alpha_n\} Bα​={α1​,α2​,...,αn​}与 B β = { β 1 , β 2 , . . . , β n } \Beta_\beta=\{\beta_1,\beta_2,...,\beta_n\} Bβ​={β1​,β2​,...,βn​}分别是 V n V^n Vn与 V m V^m Vm的基。 1）求零空间 N ( T ) N(T) N(T)的基：

2）求值空间 R ( T ) R(T) R(T)的基：

例子：