| 如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程) | 您所在的位置:网站首页 › 阻抗函数怎么求 › 如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程) |
如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程)
|
目录
如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程)一. 打颗栗子二. 求幅度1. 快速傅里叶变换2. 求出复数的绝对值3. 归一化小结
三. 求频率1. 频率公式2. 删去重复值小结
附录:完整代码附录:原理解释 & 推导过程
如何 FFT(快速傅里叶变换) 求幅度、频率(超详细 含推导过程)
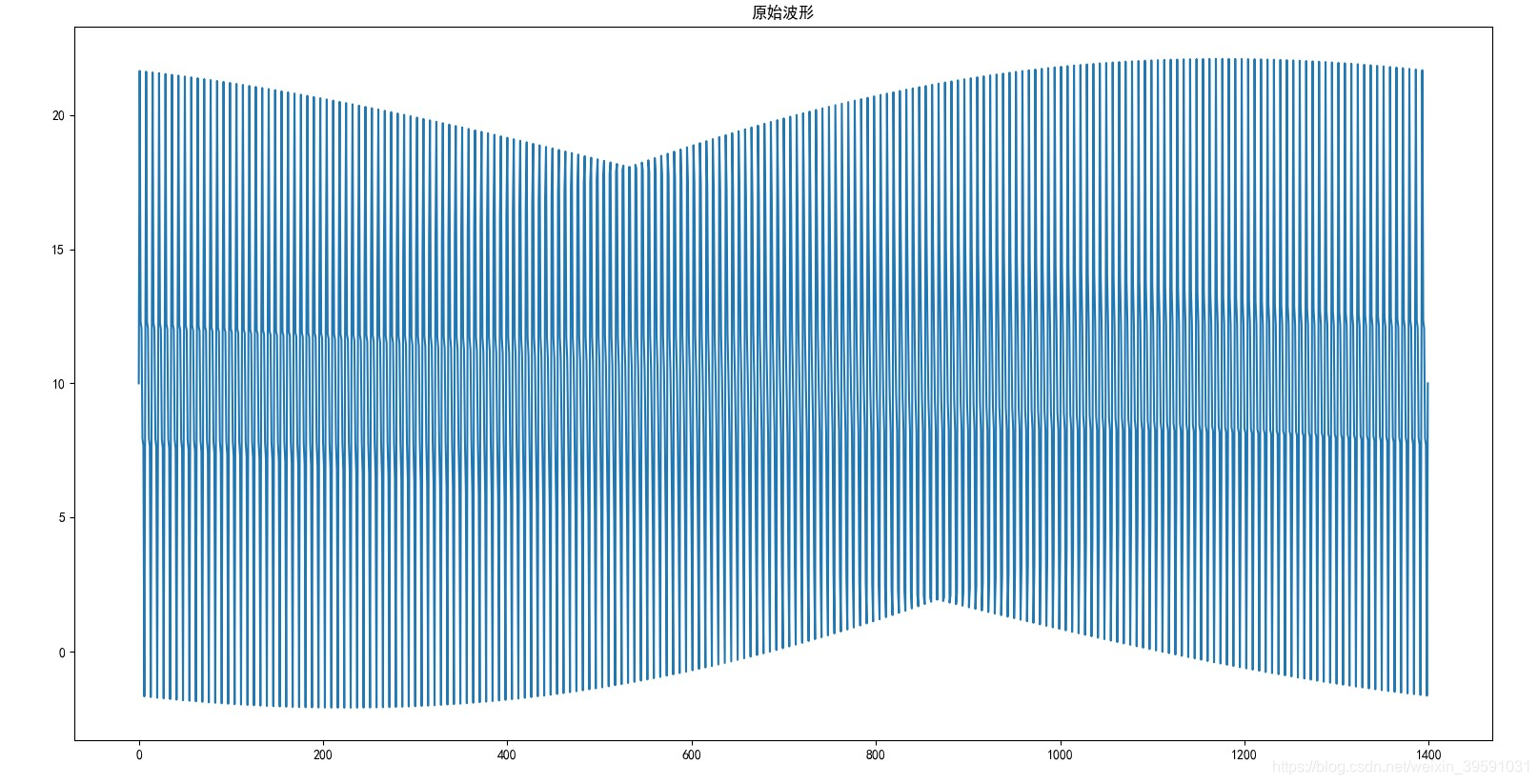
为知道这个答案查了很多资料,总结一下。 注:本文代码的头文件等如下 import numpy as np from scipy.fftpack import fft import matplotlib.pyplot as plt from matplotlib.pylab import mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文 mpl.rcParams['axes.unicode_minus'] = False # 显示负号 一. 打颗栗子我们设 采样频率为Fs信号最高频率为F采样点数为N并且有如下波形的一个信号。该信号由频率分量为0Hz,200Hz,400Hz和600Hz的四个标准正弦函数组成。 对应完整代码 # 采样点选择1400个,因为设置的信号频率分量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍, # 所以这里设置采样频率为1400赫兹(即一秒内有1400个采样点) N = 1400 # 设置1400个采样点 x = np.linspace(0, 1, N) # 将0到1平分成1400份 # 设置需要采样的信号,频率分量有0,200,400和600 y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin( 2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x) + 10 # 构造一个演示用的组合信号 plt.plot(x, y) plt.title('原始波形') plt.show()可以看出,在这个例子中 采样频率Fs信号最高频率F采样点数N1400Hz600Hz1400个 二. 求幅度 1. 快速傅里叶变换在此基础上,我们进行快速傅里叶变换(FFT),得到N个复数。每一个复数值包含着一个特定频率的信息。根据这N个复数,可以知道拆分原始信号得到的各个频率和他们的幅度值。 对应代码 fft_y = fft(y) # 使用快速傅里叶变换,得到的fft_y是长度为N的复数数组根据此数据,可以画出下面这个不是很规则的图。 (在求幅度这一节,我们先把精力集中在纵轴,横轴将在下一节求频率的时候讲解。)
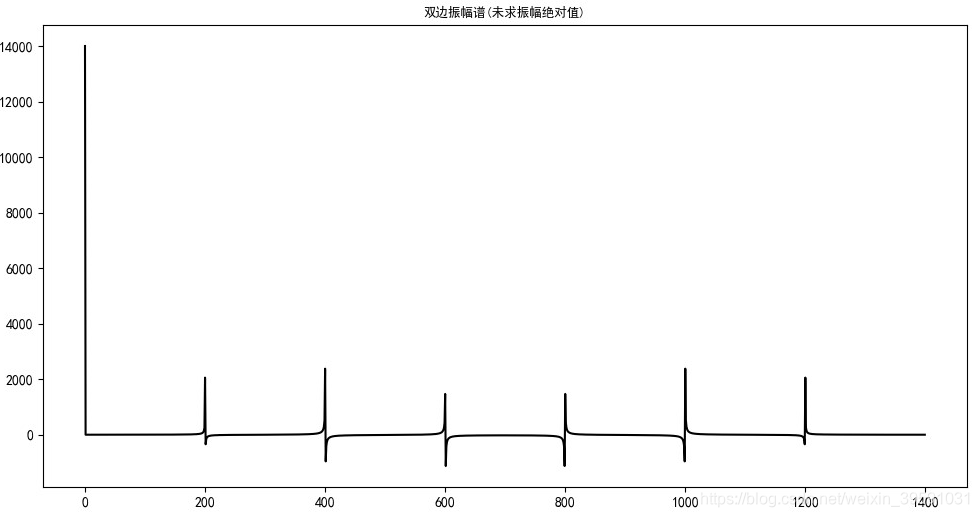
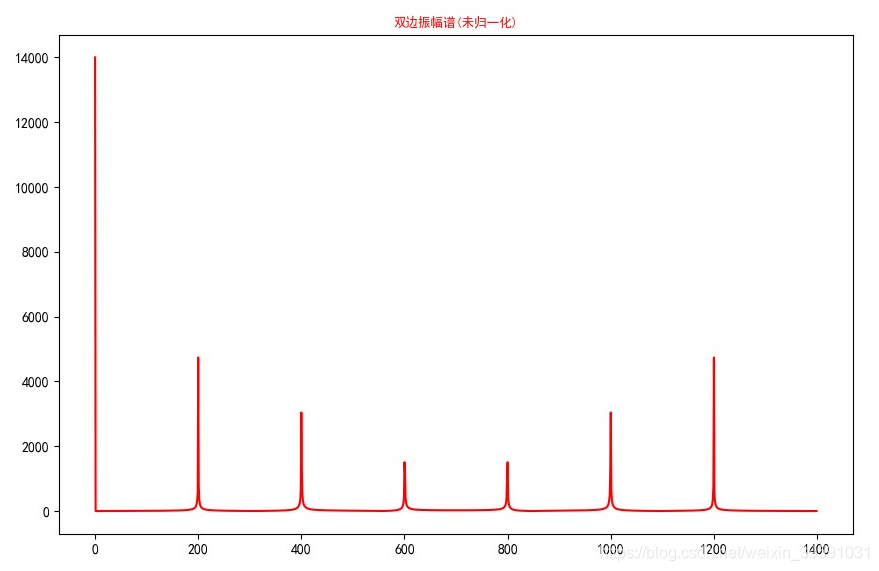
对应完整代码如下 N = 1400 # 设置1400个采样点 x = np.linspace(0, 1, N) # 将0到1平分成1400份 y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin( 2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x) + 10 # 构造一个演示用的组合信号 fft_y = fft(y) # 使用快速傅里叶变换,得到的fft_y是长度为N的复数数组 x = np.arange(N) # 频率个数 (x的取值涉及到横轴的设置,这里暂时忽略,在第二节求频率时讲解) plt.plot(x, fft_y, 'black') plt.title('双边振幅谱(未求振幅绝对值)', fontsize=9, color='black') plt.show() 2. 求出复数的绝对值用复数直接画出的图不是我们需要的。应先求出全部N个复数的绝对值(模长) abs_y = np.abs(fft_y) # 取复数的绝对值,即复数的模据此可画出下图
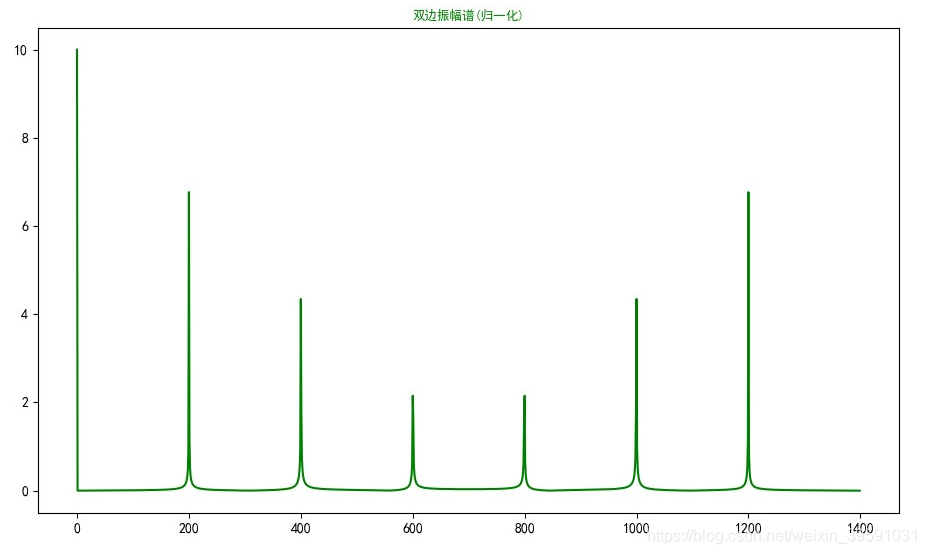
上图中,左侧第一个竖线的纵坐标值,是 从原始信号中提取出来的0Hz对应的信号强度(信号振幅),又称 直流分量。它对应的信号振幅为 当前值/FFT的采样点数N,即 0Hz对应振幅 = 当前值 / 采样点数N 注: 本例中,直流分量对应振幅 = 14000 / 1400 = 10当前值为根据当前复数求出的绝对值(模长),对应图中竖线的纵坐标最大值直流分量以外的分量所对应的信号振幅为 当前值/(采样点数N/2),即 其余频率对应的振幅 = 当前值 /(采样点数N / 2) 注: 本例中,200Hz对应振幅 = 5000 / (1400 / 2) ≈ 7.14(这里的5000是对200Hz对应纵坐标的估计值,只是为了举例,不一定准确),其余频率对应振幅算法相同。于是,在归一化后,我们得到下图
这里先放上一段文字,这段话较为形象的解释了求频率的方法。 举个例子,你有一个最高频率f = 32kHz的模拟信号,采样频率 64kHz,对这个信号做一个16个点的FFT分析,采样点下标 n 的范围是0, 1, 2, 3, …, 15。那么64kHz的模拟频率被分成了16份,每一份是4kHz,这个4kHz被称为频率分辨率。 所以,频率图的横坐标中: n=1 对应的f是4kHz n=2 对应的f是8kHz … n=15 对应的f是60kHz 而频谱是关于n=8对称的,只需关心n = 0 ~ 7的频谱就足够了。因为,原信号的最高频率是32kHz。 (本段改编自参考资料1) 1. 频率公式因此,在知道了采样频率Fs后,快速傅里叶变换(FFT)后的第x个(x从0开始)复数值对应的实际频率为 f(x) = x * (Fs / n) 于是,在这个例子中, 第0个点的频率 f(0) = 0 * (1400 / 1400) = 0 第1个点的频率 f(0) = 1 * (1400 / 1400) = 1 第2个点的频率 f(0) = 2 * (1400 / 1400) = 2 … 第200个点的频率 f(200) = 200 * (1400 / 1400) = 200 … 第1400个点的频率 f(200) = 1400 * (1400 / 1400) = 1400 (这里由于设置得很巧合,第x个点对应的频率恰好就是x) 现在便知,x轴坐标值为何如此设定。 2. 删去重复值而只有0 ~ N/2 这一半的频率是有效的,另一半与这一半对称。去重后,我们便得到下图
对应完整代码: N = 1400 # 设置1400个采样点 x = np.linspace(0, 1, N) # 将0到1平分成1400份 y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin( 2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x) + 10 # 构造一个演示用的组合信号 fft_y = fft(y) # 使用快速傅里叶变换,得到的fft_y是长度为N的复数数组 x = np.arange(N) # 频率个数(x的取值涉及到横轴的设置,这里暂时忽略,在第二节求频率时讲解) half_x = x[range(int(N / 2))] # 取一半区间 abs_y = np.abs(fft_y) # 取复数的绝对值,即复数的模 normalization_y = abs_y / (N / 2) # 归一化处理(双边频谱) normalization_y[0] /= 2 normalization_half_y = normalization_y[range(int(N / 2))] # 由于对称性,只取一半区间(单边频谱) plt.plot(half_x, normalization_half_y, 'blue') plt.title('单边振幅谱(归一化)', fontsize=9, color='blue') plt.show() 小结FFT后得到的n个复数值中,第x个(x从0开始)复数值对应的频率f(x)为 f(x) = x * (Fs / n) 附录:完整代码 import numpy as np from scipy.fftpack import fft import matplotlib.pyplot as plt from matplotlib.pylab import mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文 mpl.rcParams['axes.unicode_minus'] = False # 显示负号 # 采样点选择1400个,因为设置的信号频率分量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍, # 所以这里设置采样频率为1400赫兹(即一秒内有1400个采样点,一样意思的) N = 1400 x = np.linspace(0, 1, N) # 设置需要采样的信号,频率分量有0,200,400和600 y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin( 2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x) + 10 fft_y = fft(y) # 快速傅里叶变换 x = np.arange(N) # 频率个数 half_x = x[range(int(N / 2))] # 取一半区间 angle_y = np.angle(fft_y) # 取复数的角度 abs_y = np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱) normalization_y = abs_y / (N / 2) # 归一化处理(双边频谱) normalization_y[0] /= 2 # 归一化处理(双边频谱) normalization_half_y = normalization_y[range(int(N / 2))] # 由于对称性,只取一半区间(单边频谱) plt.subplot(231) plt.plot(x, y) plt.title('原始波形') plt.subplot(232) plt.plot(x, fft_y, 'black') plt.title('双边振幅谱(未求振幅绝对值)', fontsize=9, color='black') plt.subplot(233) plt.plot(x, abs_y, 'r') plt.title('双边振幅谱(未归一化)', fontsize=9, color='red') plt.subplot(234) plt.plot(x, angle_y, 'violet') plt.title('双边相位谱(未归一化)', fontsize=9, color='violet') plt.subplot(235) plt.plot(x, normalization_y, 'g') plt.title('双边振幅谱(归一化)', fontsize=9, color='green') plt.subplot(236) plt.plot(half_x, normalization_half_y, 'blue') plt.title('单边振幅谱(归一化)', fontsize=9, color='blue') plt.show() 附录:原理解释 & 推导过程深入浅出的原理解释视频请见:快速傅里叶变换(FFT)——有史以来最巧妙的算法□ 硬核直接的公式推导推荐这篇文章:傅里叶变换中,圆频率w与频率f之间的公式转化 参考资料: 数字信号处理中的归一化频率使用python(scipy和numpy)实现快速傅里叶变换(FFT)最详细教程FFT后得到复数,如何根据这个复数求频率?FFT之频率与幅值的确定傅里叶变换中,圆频率w与频率f之间的公式转化快速傅里叶变换(FFT)——有史以来最巧妙的算法 - 知乎 |
【本文地址】
 对应完整代码
对应完整代码