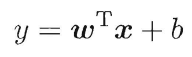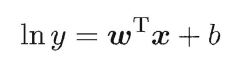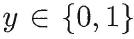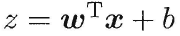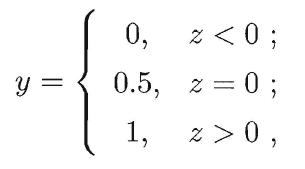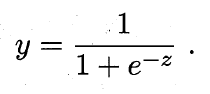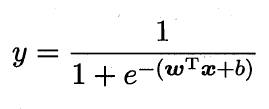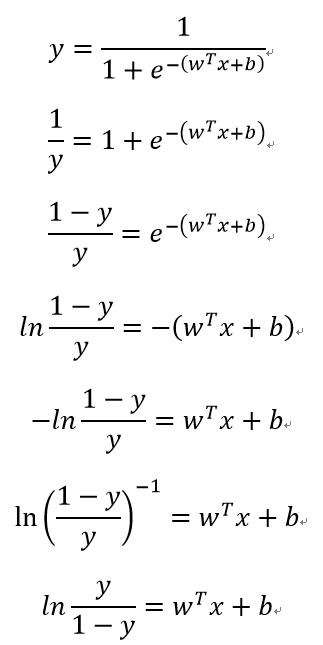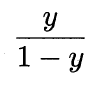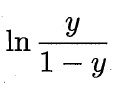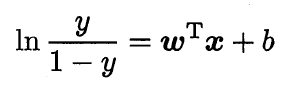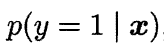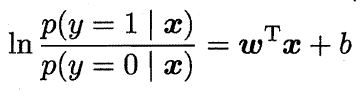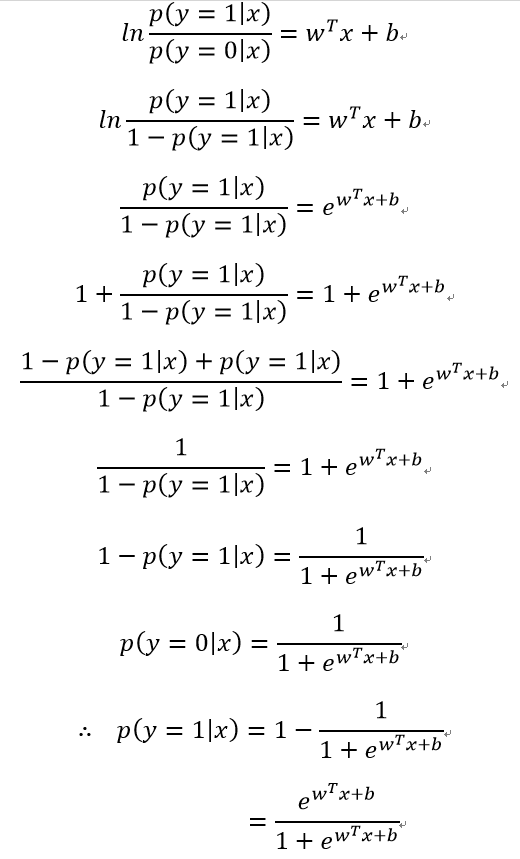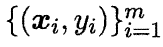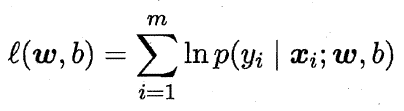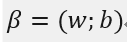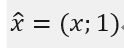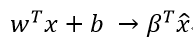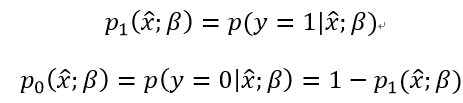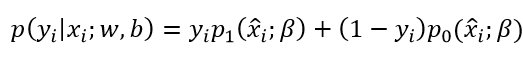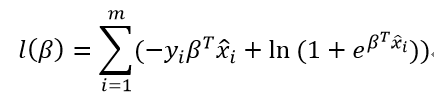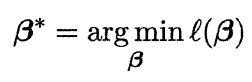| (数据科学学习手札24)逻辑回归分类器原理详解&Python与R实现 | 您所在的位置:网站首页 › 逻辑回归函数是指 › (数据科学学习手札24)逻辑回归分类器原理详解&Python与R实现 |
(数据科学学习手札24)逻辑回归分类器原理详解&Python与R实现
|
一、简介 逻辑回归(Logistic Regression),与它的名字恰恰相反,它是一个分类器而非回归方法,在一些文献里它也被称为logit回归、最大熵分类器(MaxEnt)、对数线性分类器等;我们都知道可以用回归模型来进行回归任务,但如果要利用回归模型来进行分类该怎么办呢?本文介绍的逻辑回归就基于广义线性模型(generalized linear model),下面我们简单介绍一下广义线性模型: 我们都知道普通线性回归模型的形式:
如果等号右边的输出值与左边y经过某个函数变换后得到的值比较贴切,如下面常见的“对数线性回归”(log-linear regression):
这里对数函数ln(y)起到的作用便是将y转换为其对数值,且这个对数值与右边的线性模型的预测值更为贴切接近,我们管类似这里对数函数的套在y外面的单调可微函数(因为只有单调可微函数才存在反函数)叫做“联系函数”(link function),引出下面更一般的形式:
我们在这里使用一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来; 考虑二分类任务,其输出标记:
而线性回归模型产出的预测值:
是连续域上的实值,因此我们需要把实值z转换为0/1值,最理想的是“单位阶跃函数”(unit-step function)
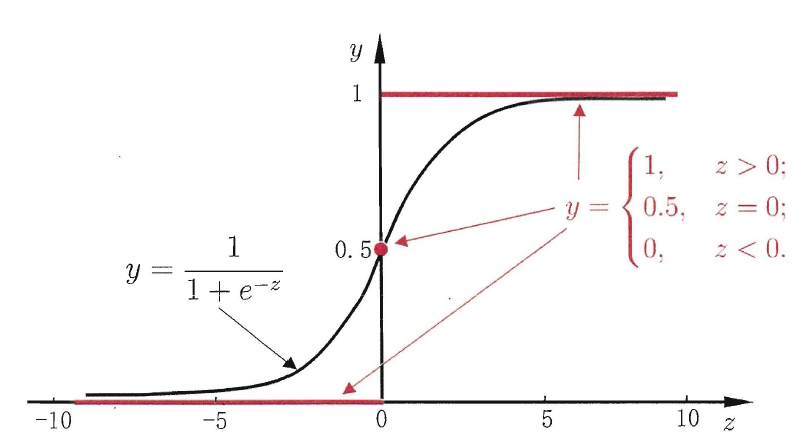
这里规定预测值z大于零就判为正例,小于零则判为反例,预测值为临界值零则可任意判别(事实上这种情况的样本本就存在一些问题而无法通过逻辑回归进行分类),下图展示了单位阶跃函数(红色)与对数几率函数(黑色):
从上图可以看出,单位阶跃函数不连续,数学性质差,因此不能直接用作广义线性模型中的link function,于是我们的目的是找到在一定程度上近似单位阶跃函数的“替代函数”(surrogate function),并希望它单调可微。对数几率函数(logistic function)正是这样一个常用的替代函数:
对数几率函数是一种“Sigmoid”函数(即形似S的函数,在神经网络的激励函数中有广泛应用),它将z值转化为一个接近0或1的y值,并且其输出值在z=0附近变化很陡。将该对数几率函数作为联系函数代入广义线性模型,可得:
我们对其进行如下推导变换:
若将y视为样本x作为正例的可能性,则1-y是其反例可能性,两者的比值:
称为“几率”(odds),反映了x作为正例的相对可能性。对几率取对数则得到“对数几率”(log odds,亦称logit):
由此可看出,这实际上是用线性回归模型的预测结果去逼近真实标记的对数几率,因此其对应的模型称为“对数几率回归”(logistic regression,亦称logit regression),这种方法具有诸多优点: 1.直接针对分类可能性进行建模,无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题; 2.不仅输出预测类别,还输出了近似的预测概率,这对许多需要利用预测概率进行辅助决策的任务很有用; 3.对率函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可直接用于求取最优解
二、训练方法 根据一个样本集训练逻辑回归模型,实际上是要得到参数w与截距b,下面我们来仔细推导训练的思想: 前面我们得到了:
将其中的y视为类后验概率估计:
则前面的式子可改写为:
下面根据上式对正例和反例的后验概率估计进行推导:
因此,我们可以通过“极大似然法”(maximum likelihood method)来估计w与b,给定数据集:
对率回归模型最大化“对数似然”(log-likelihood):
即令每个样本属于其真实标记的概率越大越好。令:
则:
再令:
则:
则最大化“对数似然”转换为:
因为上式为关于β的高阶可导连续凸函数,由凸优化理论,使用经典的数值优化算法如梯度下降法(gradient decent method)、牛顿法(Newton method)等均可求得其最优解,即得到:
则我们的逻辑回归模型训练完成。
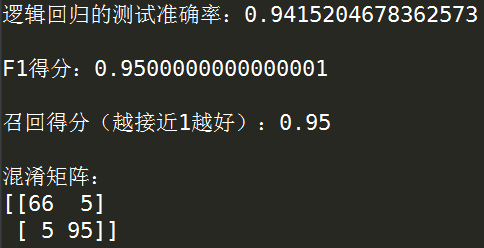
三、Python实现 我们使用sklearn.linear_model中的LogisticRegression方法来训练逻辑回归分类器,其主要参数如下: class_weight:用于处理类别不平衡问题,即这时的阈值不再是0.5,而是一个再缩放后的值; fit_intercept:bool型参数,设置是否求解截距项,即b,默认True; random_state:设置随机数种子; solver:选择用于求解最大化“对数似然”的算法,有以下几种及其适用场景: 1.对于较小的数据集,使用"liblinear"更佳; 2.对于较大的数据集,"sag"、"saga"更佳; 3.对于多分类问题,应使用"newton-cg"、"sag"、"saga"、"lbfgs"; max_iter:设置求解算法的迭代次数,仅适用于solver设置为"newton-cg"、"lbfgs"、"sag"的情况; multi_class:为多分类问题选择训练策略,有"ovr"、"multinomial" ,后者不支持"liblinear"; n_jobs:当处理多分类问题训练策略为'ovr'时,在训练时并行运算使用的CPU核心数量。当solver被设置为“liblinear”时,不管是否指定了multi_class,这个参数都会被忽略。如果给定值-1,则所有的核心都被使用,所以推荐-1,默认项为1,即只使用1个核心。 下面我们以威斯康辛州乳腺癌数据为例进行演示: from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import f1_score as f1 from sklearn.metrics import recall_score as recall from sklearn.metrics import confusion_matrix as cm '''导入威斯康辛州乳腺癌数据''' X,y = datasets.load_breast_cancer(return_X_y=True) '''分割训练集与验证集''' X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,test_size=0.3) '''初始化逻辑回归分类器,这里对类别不平衡问题做了处理''' cl = LogisticRegression(class_weight='balanced') '''利用训练数据进行逻辑回归分类器的训练''' cl = cl.fit(X_train,y_train) '''打印训练的模型在验证集上的正确率''' print('逻辑回归的测试准确率:'+str(cl.score(X_test,y_test))+'\n') '''打印f1得分''' print('F1得分:'+str(f1(y_test,cl.predict(X_test)))+'\n') '''打印召回得分''' print('召回得分(越接近1越好):'+str(recall(y_test,cl.predict(X_test)))+'\n') '''打印混淆矩阵''' print('混淆矩阵:'+'\n'+str(cm(y_test,cl.predict(X_test)))+'\n')
四、R实现 在R中实现逻辑回归的过程比较细致,也比较贴近于统计学思想,我们使用glm()来训练逻辑回归模型,这是一个训练广义线性模型的函数,注意,这种方法不像sklearn中那样主要在乎的是输出的分类结果,而是更加注重模型的思想以及可解释性(即每个变量对结果的影响程度),下面对glm()的主要参数进行介绍: formula:这里和R中常见的算法格式一样,传递一个因变量~自变量的形式; family:这个参数可以传递一个字符串或family函数形式的输入,默认为gaussian,表示拟合出的函数的误差项服从正态分布,若使用family则可同时定义误差服从的分布和广义线性模型中的联系函数,例如本文所需的逻辑回归函数,就可以有两种设定方式: 1.传入gaussian 2.传入binomial(link='logit') data:指定变量所属的数据框名称; weights:传入一个numeric型向量,用于类别不平衡问题的再缩放,默认无,即将1与0类视作平衡; model:逻辑型变量,用于控制是否输出最终训练的模型; 下面我们对威斯康辛州乳腺癌数据集进行逻辑回归分类训练,该数据集下载自https://archive.ics.uci.edu/ml/datasets.html > rm(list=ls()) > setwd('C:\\Users\\windows\\Desktop')> > #read data > data data[,1] = as.numeric(data[,1])-1 > > #spilt the datasets into train-dataset and test-dataset with a proportion of 7:3 > sam train test > #method 1 to train the logistic regression model > cl1 summary(cl1) Call: glm(formula = V2 ~ ., family = gaussian, data = train, model = T) Deviance Residuals: Min 1Q Median 3Q Max -0.5508 -0.1495 -0.0289 0.1313 0.8827 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.5799840 0.5155747 -3.065 0.002342 ** V3 -0.2599482 0.2154418 -1.207 0.228370 V4 -0.0079273 0.0095174 -0.833 0.405427 V5 0.0081528 0.0305549 0.267 0.789754 V6 0.0013896 0.0006602 2.105 0.035995 * V7 1.4228253 2.5709862 0.553 0.580315 V8 -3.6635584 1.5680864 -2.336 0.020012 * V9 0.7080702 1.2295130 0.576 0.565039 V10 3.1537615 2.3451202 1.345 0.179514 V11 0.1732304 0.8911542 0.194 0.845979 V12 -1.9387489 6.7295898 -0.288 0.773438 V13 0.7726866 0.4147097 1.863 0.063233 . V14 -0.0279811 0.0410619 -0.681 0.496025 V15 -0.1233500 0.0552559 -2.232 0.026195 * V16 0.0004280 0.0017295 0.247 0.804693 V17 12.4604521 9.3370259 1.335 0.182861 V18 3.4109051 2.5982124 1.313 0.190074 V19 -3.2029680 1.4955409 -2.142 0.032877 * V20 5.8114764 6.7403058 0.862 0.389142 V21 6.3245471 3.5132301 1.800 0.072649 . V22 -3.8548911 13.9312795 -0.277 0.782160 V23 0.2085364 0.0725441 2.875 0.004281 ** V24 0.0163053 0.0082144 1.985 0.047892 * V25 0.0103947 0.0073762 1.409 0.159613 V26 -0.0015405 0.0004029 -3.823 0.000155 *** V27 0.3199127 1.7892352 0.179 0.858195 V28 -0.2059715 0.5003384 -0.412 0.680826 V29 0.3228923 0.3129524 1.032 0.302863 V30 0.4349610 1.1458239 0.380 0.704458 V31 0.0973530 0.6204197 0.157 0.875398 V32 3.6376056 2.9501115 1.233 0.218350 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for gaussian family taken to be 0.0537472) Null deviance: 91.048 on 397 degrees of freedom Residual deviance: 19.725 on 367 degrees of freedom AIC: -2.3374 Number of Fisher Scoring iterations: 2 > pre predict 0.5,1,0)) > #print the confusion matrix > table(predict) predict true 0 1 0 99 1 1 10 61 > #print the accuracy > cat('Accuracy:',sum(diag(prop.table(table(predict)))),'\n') Accuracy: 0.9356725 > > #method 2 to train the logistic regression model > cl2 summary(cl2) Call: glm(formula = V2 ~ ., family = binomial(link = "logit"), data = train, model = T) Deviance Residuals: Min 1Q Median 3Q Max -2.220e-04 -2.100e-08 -2.100e-08 2.100e-08 2.033e-04 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -8.758e+02 8.910e+05 -0.001 0.999 V3 -2.024e+02 1.990e+05 -0.001 0.999 V4 3.032e+00 9.058e+03 0.000 1.000 V5 4.306e+01 2.243e+04 0.002 0.998 V6 2.976e-01 8.733e+02 0.000 1.000 V7 5.400e+03 1.824e+06 0.003 0.998 V8 -6.629e+03 9.677e+05 -0.007 0.995 V9 4.722e+03 1.151e+06 0.004 0.997 V10 -1.708e+03 2.175e+06 -0.001 0.999 V11 -1.363e+03 6.115e+05 -0.002 0.998 V12 6.584e+03 7.757e+06 0.001 0.999 V13 -2.640e+01 6.282e+05 0.000 1.000 V14 -1.098e+02 7.760e+04 -0.001 0.999 V15 1.270e+02 1.013e+05 0.001 0.999 V16 4.578e+00 5.046e+03 0.001 0.999 V17 -1.474e+04 6.903e+06 -0.002 0.998 V18 1.068e+04 3.621e+06 0.003 0.998 V19 -5.032e+03 8.410e+05 -0.006 0.995 V20 4.981e+02 6.488e+06 0.000 1.000 V21 -1.025e+04 3.006e+06 -0.003 0.997 V22 -6.005e+04 2.600e+07 -0.002 0.998 V23 -2.170e+01 5.623e+04 0.000 1.000 V24 1.412e+01 1.030e+04 0.001 0.999 V25 -1.807e+01 7.861e+03 -0.002 0.998 V26 4.411e-01 4.646e+02 0.001 0.999 V27 4.996e+02 9.163e+05 0.001 1.000 V28 -4.239e+02 4.489e+05 -0.001 0.999 V29 1.159e+02 1.815e+05 0.001 0.999 V30 1.786e+03 1.018e+06 0.002 0.999 V31 2.349e+03 3.750e+05 0.006 0.995 V32 -8.331e+02 3.861e+06 0.000 1.000 (Dispersion parameter for binomial family taken to be 1) Null deviance: 5.1744e+02 on 397 degrees of freedom Residual deviance: 4.1036e-07 on 367 degrees of freedom AIC: 62 Number of Fisher Scoring iterations: 25 > pre predict 0.5,1,0)) > #print the confusion matrix > table(predict) predict true 0 1 0 94 6 1 7 64 > #print the accuracy > cat('Accuracy:',sum(diag(prop.table(table(predict)))),'\n') Accuracy: 0.9239766
可以看出,方法1效果更佳;
以上就是关于逻辑回归的基本内容,今后也会不定时地在本文中增加更多内容,敬请期待。
|
【本文地址】