| 数值分析实验四 线性方程组数值解法 | 您所在的位置：网站首页 › 贝克德尔实验结果分析 › 数值分析实验四 线性方程组数值解法 |
数值分析实验四 线性方程组数值解法
|
一、实验目的
1、熟悉求解线性方程组的有关理论和方法； 2、会编制LU 分解法、雅可比及高斯—塞德尔迭代法德程序； 3、通过实际计算，进一步了解各种方法的优缺点，选择合适的数值方法。 二、算法描述3.1 矩阵直接三角分解法 算法 将方程组Ax=b 中的A分解为A=LU，其中L为单位下三角矩阵，U为上三角矩阵，则方程组Ax=b化为解2个方程组Ly=b，Ux=y，具体算法如下： 1、矩阵直接三角分解法 #include #include #include using namespace std; /* 1 2 -12 8 5 4 7 -2 -3 7 9 5 6 -12 -8 3 27 4 11 49 */ int main() { cout u[i] = new double[n + 1]; } for (int i = 1; i u[i][j]=0; } } //单位下三角矩阵 double** l = new double* [n + 1]; for (int i = 0; i for (int j = 1; j for (int j =1 ; j cin >> b[i]; } for (int j = 1; j l[i][1] = a[i][1]*1.0 / a[1][1]; } for (int k = 1; k u[k][j] = a[k][j]; for (int q = 1; q l[i][k] = a[i][k]; for (int q = 1; q y[k] = b[k]; for (int q = 1; q x[k] = y[k]; for (int q = k + 1; q cout a[i] = new int[n + 1]; } double* b = new double[n + 1]; cout cin >> a[i][j]; } } for (int i = 1; i if (i == j && a[i][j] == 0) { cout x[i] = new double[count+1]; } double* x1 = new double[n + 1];//最终结果 //设置初始向量 for (int i = 1; i int sum = 0; for (int i = 1; i if (j != i) { x[i][k + 1] -= a[i][j] * x[j][k]; } } x[i][k + 1] /= a[i][i]; x1[i-1] = x[i][k + 1]; sum += abs(x[i][k + 1] - x[i][k]); } if (sum >= e) { if (k >= count) { //cout cout a[i] = new int[n + 1]; } double* b = new double[n + 1]; cout cin >> a[i][j]; } } for (int i = 1; i if (i == j && a[i][j] == 0) { cout x[i] = new double[count + 1]; } double* x1 = new double[n + 1];//最终结果 //设置初始向量 for (int i = 1; i int sum = 0; for (int i = 1; i x[i][k + 1] -= a[i][j] * x[j][k+1]; } for (int j = i+1; j if (k >= count) { //cout cout |
3.2 迭代法 3.2.1 雅可比迭代法 算法:设方程组Ax=b系数矩阵的对角线元素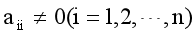
,M为迭代次数容许的最大值,ε为容许误差。 
3.2.2 高斯-塞尔德迭代法 算法:设方程组Ax=b的系数矩阵的对角线元素,
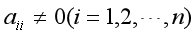,M为迭代次数容许的最大值,ε为容许误差 
【本文地址】
公司简介
联系我们