分段概率密度矩估计

在参数估计问题中，假定总体分布形式已知，未知的仅仅是一个或几个参数.

参数估计问题的一般提法

设有一个统计总体，总体的分布函数为

向量).现从该总体抽样，得样本

要依据该样本对参数θ作出估计，或估计θ的某个已知函数

这类问题称为参数估计.

假如我们要估计某队男生的平均身高.(假定身高服从正态分布N(μ,0.12))

现从该总体选取容量为5的样本，我们的任务是要根据选出的样本(5个数)求出总体均值μ的估计.而全部信息就由这5个数组成，设这5个数是:1.65，1.67，1.68，1.78，1.69

估计μ为1.68,这是点估计.

估计μ在区间[1.57, 1.84]内，这是区间估计.

一、点估计概念及讨论的问题

例1已知某地区新生婴儿的体重

而全部信息就由这100个数组成.据此，我们应如何估计u和σ呢?

为估计u，我们需要构造出适当的样本的函数

请注意，被估计的参数

我们知道，服从正态分布

自然想到把样本体重的平均值作为总体平均体重的一个估计.

用样本体重的均值

1.矩估计法

它是基于一种简单的“替换”思想建立起来的一种估计方法.

是英国统计学家K.皮尔逊最早提出的.其基本思想是用样本矩估计总体矩,理论依据:大数定律

记总体k阶矩为

样本k阶矩为

记总体k阶中心矩为

样本k阶中心矩为

用相应的样本矩去估计总体矩的估计方法,就称为矩估计法.

矩估计步骤：

设总体的分布函数中含有k个未知参数

(1)建立

前k阶一般都是这k个参数的函数,记为:

(2)从这k个方程中解出

(3)那么以样本各阶矩

例2设总体X的概率密度为

其中

解:数学期望是一阶原点矩

由矩法，样本矩

从中解得

例3设

解:由密度函数知,X一μ具有均值为θ的指数分布

故

即

解的：

矩法的优点是简单易行，并不需要事先知道总体是什么分布.

缺点是，当总体类型已知时，没有充分利用分布提供的信息.一般场合下，矩估计量不具有唯一性.

其主要原因在于建立矩法方程时，选取那些总体矩用相应样本矩代替带有一定的随意性.

是在总体类型已知条件下使用的一种参数估计方法。

它首先是由德国数学家高斯在1821年提出的，然而，这个方法常归功于英国统计学家费歇.

费歇在1922年重新发现了这一方法，并首先研究了这种方法的一些性质.

极大似然法的基本思想

先看一个简单例子:某位同学与一位猎人一起外出打猎.一只野兔从前方窜过.只听一声枪响，野兔应声倒下.

如果要你推测，是谁打中的呢?你会如何想呢?

你就会想，只发一枪便打中,猎人命中的概率一般大于这位同学命中的概率.看来这一枪是猎人射中的

这个例子所作的推断已经体现了极大似然法的基本思想，

下面我们再看一个例子，进一步体会 极大似然法的基本思想，

极大似然估计原理:

设

当给定样本

极大似然估计法就是用使

称

求极大似然估计(MLE)的一般步骤是:

(1)由总体分布导出样本的联合概率函数(或联合密度);

(2)把样本联合概率函数(或联合密度)中自变量看成已知常数,而把参数θ看作自变量，得到似然函数

(3)求似然函数

两点说明:

1、求似然函数L( θ)的最大值点，可以应用微积分中的技巧。由于In(x)是x的增 函数，

可以得到

若

2、用上述求导方法求参数的MLE有时行不通，这时要用极大似然原则来求.

下面举例说明如何求极大似然估计

例6、设

解:似然函数为

对p求导并令其为0,

得，

例7设

解:似然函数为

对数似然函数为

对

得，

例8设

解:似然函数为

对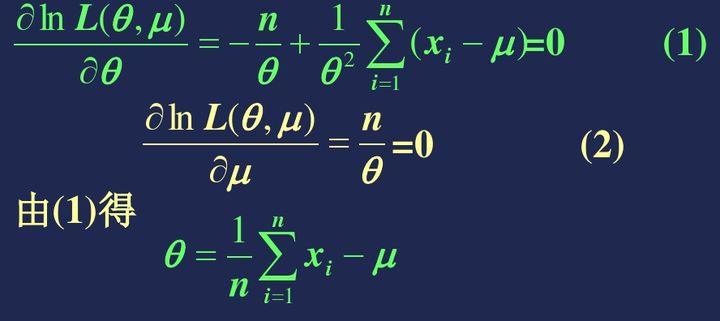

用求导方法无法最终确定

对

μ取其它值时,

于是

极大似然估计的一个性质

可证明极大似然估计具有下述性质:

设