| 【Unity】Unity 几何知识、弧度、三角函数、向量运算、点乘、叉乘 | 您所在的位置:网站首页 › 计算机算sin30 › 【Unity】Unity 几何知识、弧度、三角函数、向量运算、点乘、叉乘 |
【Unity】Unity 几何知识、弧度、三角函数、向量运算、点乘、叉乘
|
文章目录
基础几何知识角的度量方式角度弧度转换三角函数计算公式常用三角函数值使用方法Unity应用
向量向量加减法向量相减向量相加向量与标量的乘除点乘叉乘叉乘获得垂直向量左手规则叉乘计算角度
计算360°以内的角(点乘结合叉乘)Vector3
基础几何知识
角的度量方式
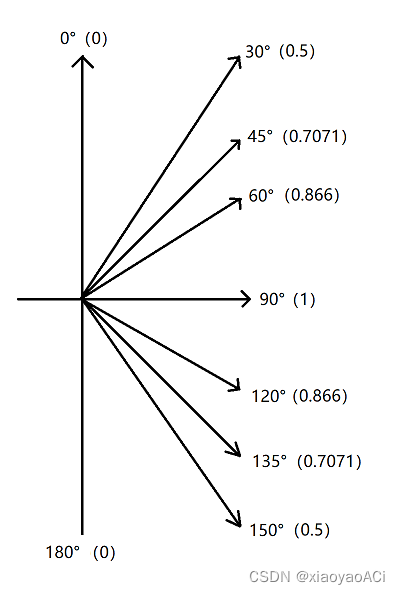
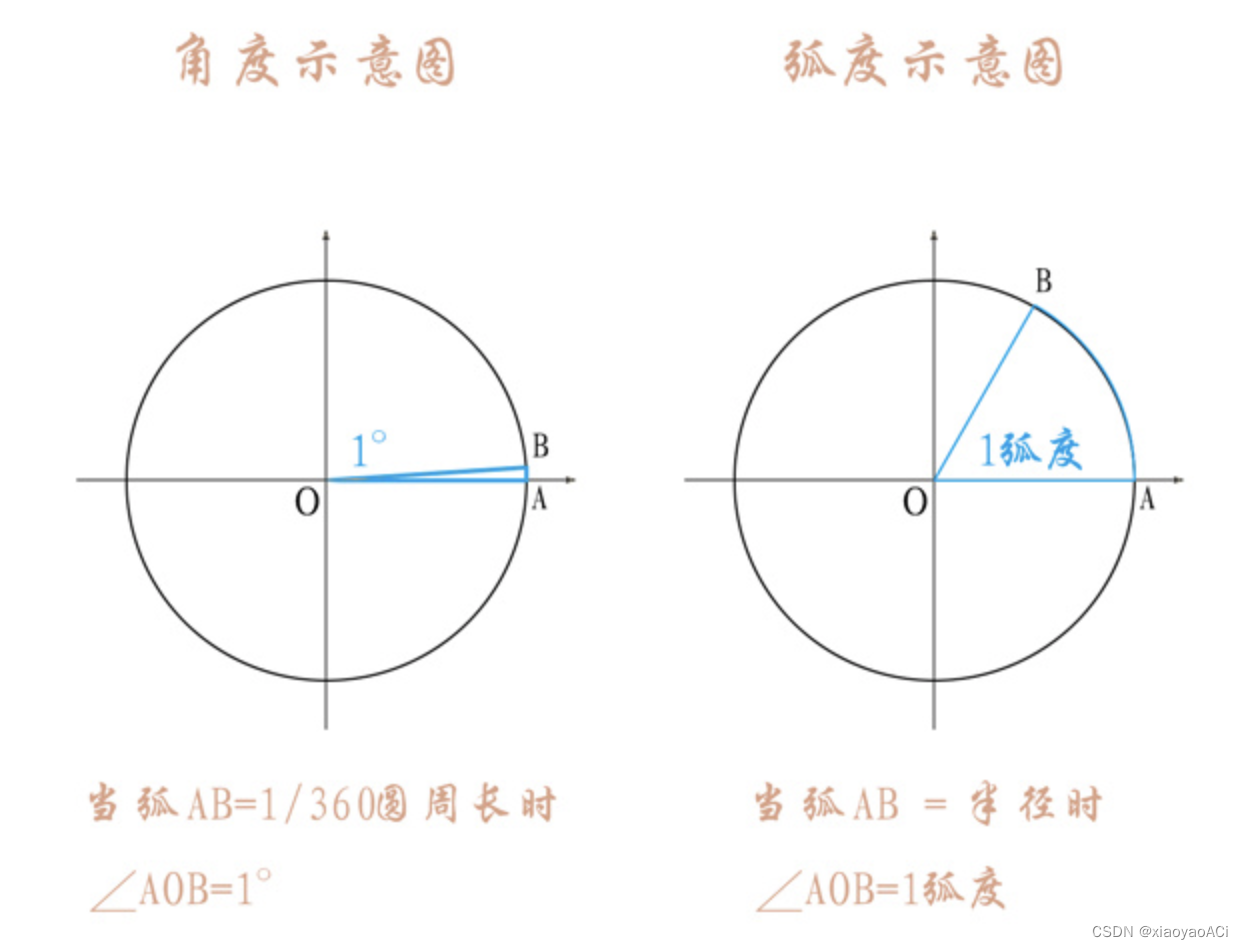
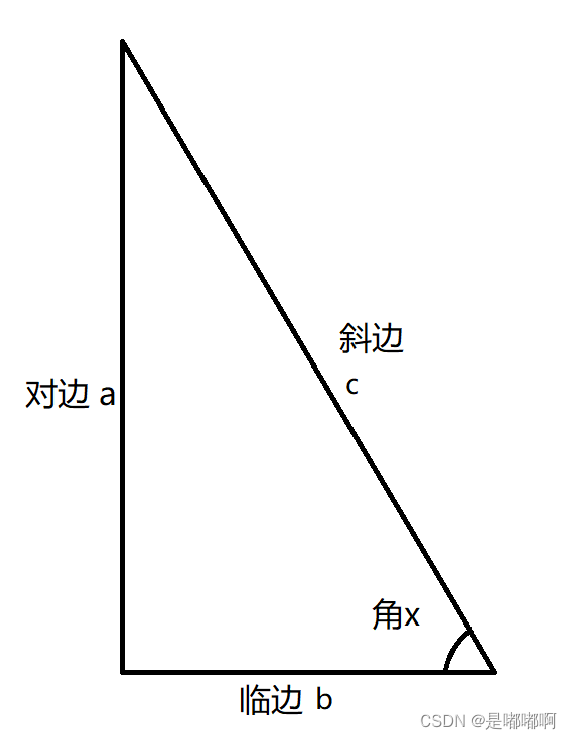
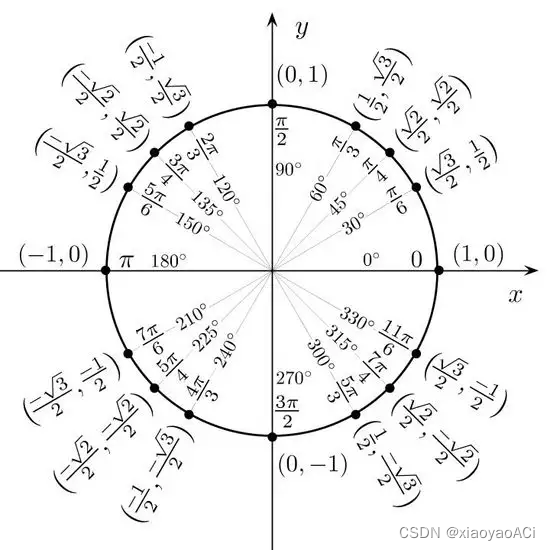
角的度量方式分为角度(Degree)和弧度(Radian)两种。角度就是将一个圆形切成360份,每一份就是1度角。弧度是当弧长等于圆的半径时即为1弧度。 如图所示: 常用换算: π = 180 度 \ \pi = 180度 π=180度 1 弧 度 = 180 度 / π \ 1弧度 = 180度 / \pi 1弧度=180度/π 1 角 度 = π / 180 度 \ 1角度 = \pi / 180度 1角度=π/180度 角度转弧度: 转换公式: 弧 度 = 角 度 数 ∗ π / 180 \ 弧度 = 角度数 * \pi / 180 弧度=角度数∗π/180Unity代码:radian = x * Mathf.Deg2Rad;弧度转角度: 转换公式: 角 度 = 弧 度 数 ∗ 180 / π \ 角度 = 弧度数 * 180 / \pi 角度=弧度数∗180/πUnity代码:degree = x * Mathf.Rad2Deg; 三角函数在直角三角形中(下图为例),如果 a 、 b 、 c 、 x \ a、b、c、x a、b、c、x中的两个变量已知则能计算出另外两个变量的值。
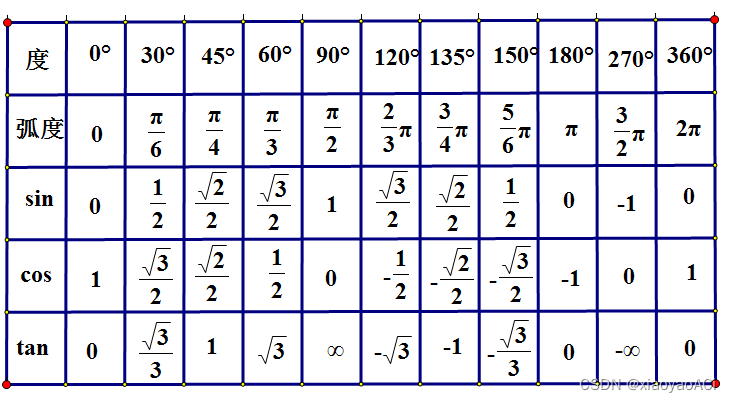
正弦: s i n ( x ) = a / c \ sin(x) = a / c sin(x)=a/c (对比斜) 余弦: c o s ( x ) = b / c \ cos(x) = b / c cos(x)=b/c (临比斜) 正切: t a n ( x ) = a / b \ tan(x) = a / b tan(x)=a/b (对比临) 余切: c o t ( x ) = b / a \ cot(x) = b / a cot(x)=b/a 正割: s e c ( x ) = c / b \ sec(x) = c / b sec(x)=c/b 余割: c s c ( x ) = c / a \ csc(x) = c / a csc(x)=c/a 反正弦: a r c s i n ( a / c ) = x \ arcsin(a / c) = x arcsin(a/c)=x 反余弦: a r c c o s ( b / c ) = x \ arccos(b / c) = x arccos(b/c)=x 反正切: a r c t a n ( a / b ) = x \ arctan(a / b) = x arctan(a/b)=x 已知一角和一边,求另外两边,用sin、cos、tan。 已知两边,求角,用arcsin、arccos、arctan。 常用三角函数值
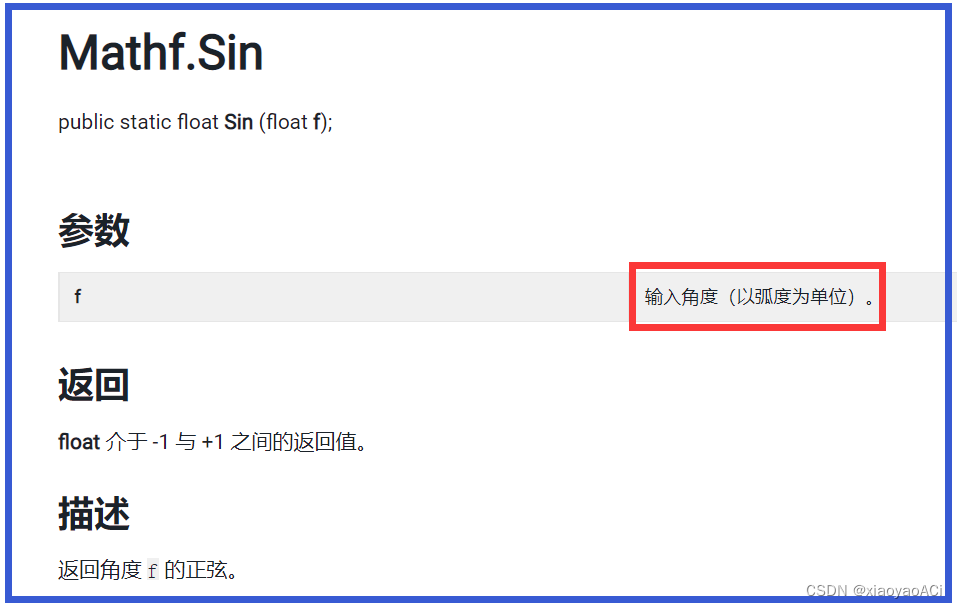
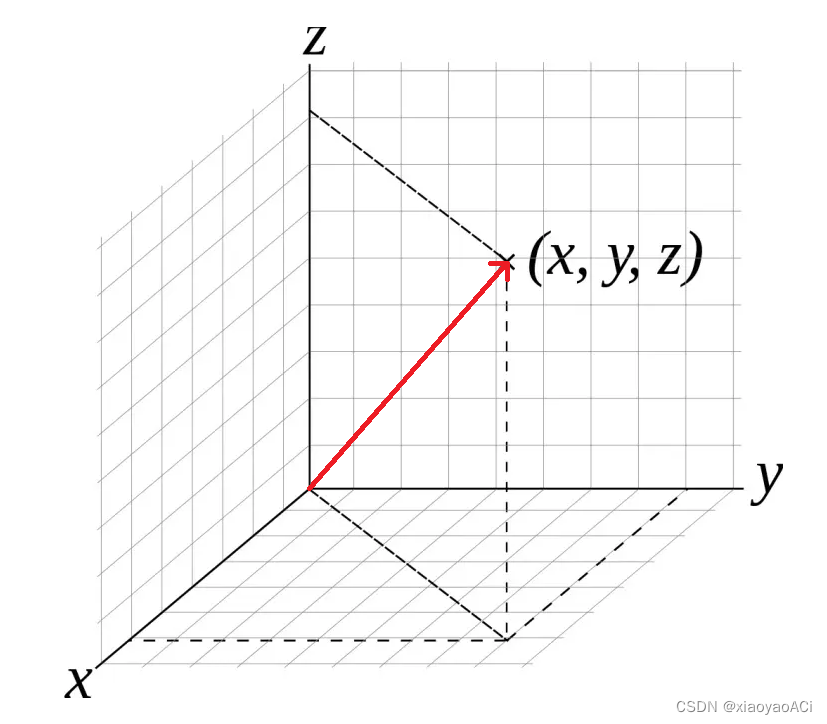
已知一个角和一条边,用 s i n 、 c o s 、 t a n \ sin、cos、tan sin、cos、tan 。 已知两条边求角度,用 A r c S i n 、 A r c C o s 、 A r c T a n \ ArcSin、ArcCos、ArcTan ArcSin、ArcCos、ArcTan 。 Unity应用在代码中调用Mathf.Sin等三角函数方法时传入的参数并不是角度,而是弧度。 比如如果我们想要获取sin30度的值不能这样写:Mathf.Sin(30)。这样是错的。 正确的写法应该是Mathf.Sin(30 * Mathf.Deg2Rad),将角度转为弧度再传参,得到的结果就是0.5了。 下图为官方API的描述。 要求输入的角度是以弧度为单位的,所以要用这些方法时经常要用到角度和弧度的转换。 向量向量是一个数字列表,表示各个维度上的有向位移。它是一个有大小有方向的物理量。大小就是方向的模长,方向描述了空间中向量的指向。向量可以用来表示物体的位置和方向。 向量的大小:也就是向量的长度(一般称作为 模),向量a的模记为 ∣ a ⃗ ∣ \ | \vec a | ∣a ∣ ,若 a ⃗ = ( x , y , z ) \ \vec a = (x, y, z) a =(x,y,z) 则 ∣ a ⃗ ∣ = x 2 + y 2 + z 2 \ | \vec a | = \sqrt {x^2 + y^2 + z^2} ∣a ∣=x2+y2+z2 。代码中使用myVector.magnitude来获取向量的大小。 单位向量:即模为1的向量,在Unity中单位向量也就代表了向量的方向。可以记作 a ^ \widehat{a} a 。一个向量的单位向量,可以通过除以它模得到,即 a ^ = a ⃗ ∣ a ⃗ ∣ \widehat{a} = \frac {\vec a} {| \vec a |} a =∣a ∣a 。代码中使用myVector.normalized来获取向量的单位向量,也就是向量的方向。 零向量:即模为0的向量,零向量的方向是任意的。 相反向量:长度相等方向相反的向量, a ⃗ \ \vec a a 的相反向量为 − a ⃗ \ -\vec a −a 。 平行(共线)向量:方向相同或相反的非零向量,记作 a ⃗ / / b ⃗ \ \vec a // \vec b a //b 。 向量加减法向量的加减就是向量对应分量的加减,类似于物理学中力的正交分解。 向量相减等于各分量相减。 [ x 1 , y 1 , z 1 ] − [ x 2 , y 2 , z 2 ] = [ x 1 − x 2 , y 1 − y 2 , z 1 − z 2 ] \ [x1,y1,z1] - [x2,y2,z2] = [x1-x2 , y1-y2 , z1-z2] [x1,y1,z1]−[x2,y2,z2]=[x1−x2,y1−y2,z1−z2] 几何意义:向量a与向量b相减,结果理解为以b的终点为起点,以a的终点为终点的向量。方向由b指向a。 注意:我们可以把向量相减理解为a、b终点的连接,但实际上该向量准确起始位置应该是坐标原点。 实际应用:计算两点之间的距离和相对方向。 向量相加向量相加等于各分量相加。 [ x 1 , y 1 , z 1 ] + [ x 2 , y 2 , z 2 ] = [ x 1 + x 2 , y 1 + y 2 , z 1 + z 2 ] \ [x1,y1,z1] + [x2,y2,z2] = [x1+x2 , y1+y2 , z1+z2] [x1,y1,z1]+[x2,y2,z2]=[x1+x2,y1+y2,z1+z2] 几何意义:如下图,假设空间中有两个向量a和b,a与a’平行且长度相等,b与b’平行且长度相等。a+b就相当于a,b,a’,b’所围成的平行四边形的对角线。 实际应用:物体的移动。 向量与标量的乘除乘法:该向量的各分量与标量相乘
k
[
x
,
y
,
z
]
=
[
x
k
,
y
k
,
z
k
]
\ k[x, y, z] = [xk, yk, zk]
k[x,y,z]=[xk,yk,zk] 。 除法:该向量的各分量与标量相除
[
x
,
y
,
z
]
/
k
=
[
x
/
k
,
y
/
k
,
z
/
k
]
\ [x, y, z]/k = [x/k , y/k , z/k]
[x,y,z]/k=[x/k,y/k,z/k] 。 几何意义:缩放向量长度。 点乘又称点积或内积。表示为各分量的乘积和。 [ x 1 , y 1 , z 1 ] ⋅ [ x 2 , y 2 , z 2 ] = x 1 x 2 + y 1 y 2 + z 1 z 2 \ [x1,y1,z1] \cdot [x2,y2,z2] = x1x2+y1y2+z1z2 [x1,y1,z1]⋅[x2,y2,z2]=x1x2+y1y2+z1z2 注意结果不是一个向量,而是一个标量(Scalar),可以是负数。 几何意义: a ⋅ b = ∣ a ∣ ∣ b ∣ cos ( a , b ) \ a \cdot b = |a||b|\cos(a, b) a⋅b=∣a∣∣b∣cos(a,b) 当a、b的模为1时,ab的点乘值为∠ab的cos值,再通过反余弦就可以获得角度。 // 计算点乘值 float dot = Vector3.Dot(a.position.normalized, b.position.normalized); // 计算夹角 float angle = Mathf.Acos(dot) * Mathf.Rad2Deg;第一步计算点乘值,第二步计算夹角。 实际应用:计算两向量的夹角。 点乘常用结果:对于标准化后的向量,方向相同,则点乘为1;方向相反,则点乘为-1;互相垂直,则点乘为0。 总结:点乘可以用于计算向量夹角,但只能用于计算内夹角,也就是小于180°的夹角。若想超过180°,则需要与叉乘结合。点乘的结果为单个数值。 叉乘叉乘又称 “叉积” 或 “外积” ,与点乘结果不同,叉乘结果是一个向量,一个垂直于两个向量所组成平面的向量。模长为两向量模长乘积再乘夹角的正弦值。 公式: [ x 1 , y 1 , z 1 ] × [ x 2 , y 2 , z 2 ] = [ y 1 ∗ z 1 − z 1 ∗ y 2 , z 1 ∗ x 2 − x 1 ∗ z 2 , x 1 ∗ y 2 − y 1 ∗ x 2 ] \ [x1,y1,z1] \times [x2,y2,z2] = [y1*z1 - z1*y2 , z1*x2 - x1*z2 , x1*y2 - y1*x2] [x1,y1,z1]×[x2,y2,z2]=[y1∗z1−z1∗y2,z1∗x2−x1∗z2,x1∗y2−y1∗x2] 代码:Vector3 cross = Vector3.Cross(a.position, b.position); 注意:叉乘不需要加normalized,加不加都不会影响结果。 应用: 创建垂直于平面的向量;判断两条向量的相对位置。 叉乘获得垂直向量当 a 到 b 顺时针,则 a x b 朝上。 当 a 到 b 逆时针,则 a x b 朝下。 代码判断:叉乘结果 y > 0 ,则朝上,则小于180°;叉乘结果 y < 0 ,则朝下,则大于180°; 左手规则a、b向量叉乘获得的垂直向量遵循左手规则,以下图为例: 叉乘也可以用来计算角度,但只能计算0° ~ 90°。 // 计算叉乘结果,叉乘不需要加normalized,但加了也不会有影响 Vector3 cross = Vector3.Cross(a.position, b.position); // 用叉乘结果换算角度 float angle = Mathf.Asin(cross.magnitude) * Mathf.Rad2Deg;叉乘常用结果: 点乘结合叉乘,可以计算出360°以内的角。 |
【本文地址】
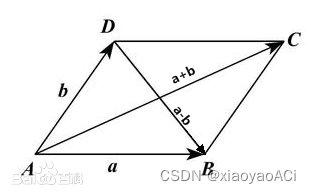
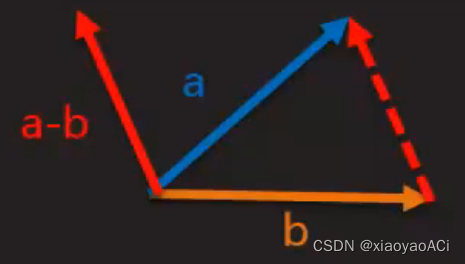
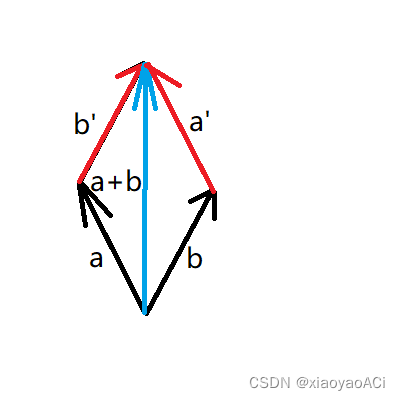 也可以这么说,由向量a的起点出发,沿着a的方向走a的长度,然后沿着b的方向走b的长度,达到的点相当于从a的起点沿着a+b的方向走a+b的长度。
也可以这么说,由向量a的起点出发,沿着a的方向走a的长度,然后沿着b的方向走b的长度,达到的点相当于从a的起点沿着a+b的方向走a+b的长度。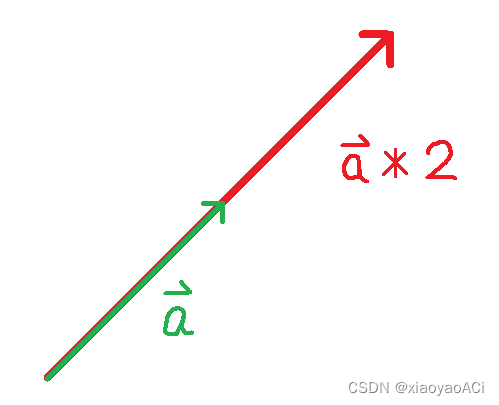 实际应用:加速、减速、放大、缩小。
实际应用:加速、减速、放大、缩小。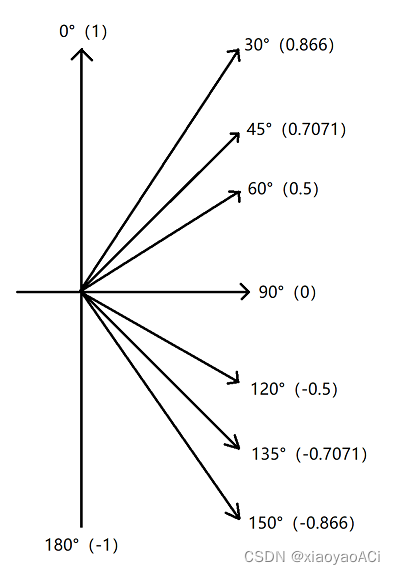
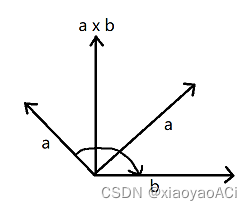
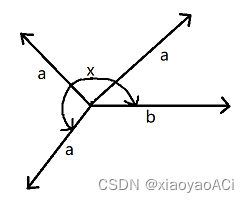
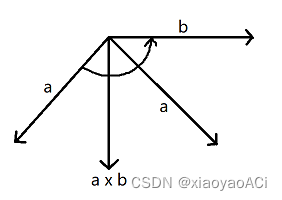 也可以这样理解:当a、b顺时针夹角小于180时, a x b 朝上;当a、b顺时针夹角大于180时, a x b 朝下。
也可以这样理解:当a、b顺时针夹角小于180时, a x b 朝上;当a、b顺时针夹角大于180时, a x b 朝下。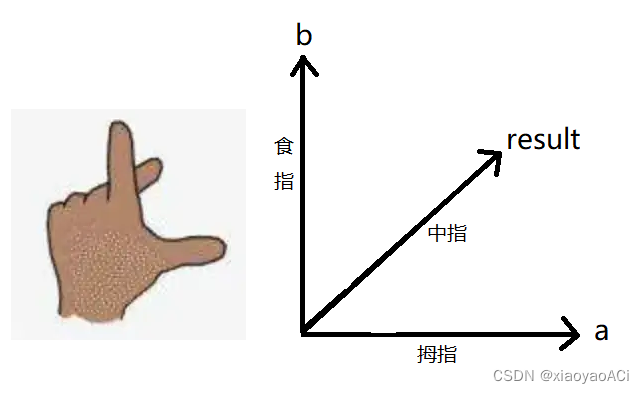 以上图手势为标准,垂直于拇指a和食指b形成的平面的向量result就是a、b叉乘的结果。
以上图手势为标准,垂直于拇指a和食指b形成的平面的向量result就是a、b叉乘的结果。