| 【数字逻辑】学习笔记 第四章 组合逻辑电路 | 您所在的位置:网站首页 › 编码器是常用的组合逻辑电路 › 【数字逻辑】学习笔记 第四章 组合逻辑电路 |
【数字逻辑】学习笔记 第四章 组合逻辑电路
|
文章目录
一、组合逻辑电路概述二、组合逻辑电路分析三、组合逻辑电路设计四、实际练习
一、组合逻辑电路概述
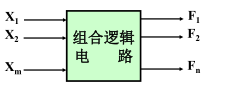
数字逻辑电路 组合逻辑电路时序逻辑电路组合电路特点 功能上:输出仅与该时刻的输入有关结构上:由门电路组成主要内容 组合电路的分析、设计方法(对小规模集成电路)常用集成组合逻辑电路(对中规模集成电路)组合逻辑电路:输出跟随输入的变化 逻辑关系: F 1 = f 1 ( X 1 , X 2 , . . . , X m ) F 2 = f 2 ( X 1 , X 2 , . . . , X m ) F n = f n ( X 1 , X 2 , . . . , X m ) \begin{aligned} F_1 &= f_1(X_1,X_2,...,X_m)\\ F_2 &= f_2(X_1,X_2,...,X_m)\\ F_n &= f_n(X_1,X_2,...,X_m)\\ \end{aligned} F1F2Fn=f1(X1,X2,...,Xm)=f2(X1,X2,...,Xm)=fn(X1,X2,...,Xm) 组合电路的特点: : 电路中不包含记忆元件输出无反馈到输入的回路任意时刻 , 电路的输出仅取决于当时的输入 二、组合逻辑电路分析分析目的 找出输出函数与输入变量的逻辑关系,确定电路所实现的逻辑功能 分析方法从输入级开始,逐级写出门的逻辑表达式对表达式进行化简列真值表描述电路的逻辑功能组合逻辑电路的级数:输入信号从输入端到输出端所经历的逻辑门的最大数目 
例1:试分析下图所示逻辑电路的功能。 例2 :试分析图中所示逻辑电路的功能。 因此,该电路为少数服从多数电路,也称多数表决电路。 例3:试分析图中所示电路逻辑,写出表达式。 设计目标: 根据逻辑功能的要求,得到实现该功能的最优逻辑电路。最优标准: 小规模 SSI —— 逻辑门数最少, 逻辑门级数最少, 逻辑门之间的连线最少中大规模 MSI —— 集成块数最少设计方法 传统方法 —— 用逻辑函数实现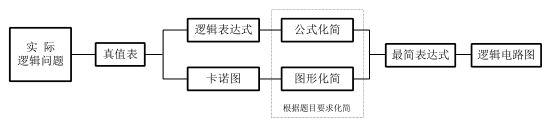 编程方法 —— 用硬件描述语言编程实现 编程方法 —— 用硬件描述语言编程实现
例1 在举重比赛中,有两名副裁判,一名主裁判。 当两名以上裁判(必须包括主裁判在内)认为运动员上举杠铃合格,按动电钮,裁决合格信号灯亮,则该运动员成绩有效。试设计该电路。 解: (1)确定输入输出:根据题意,有 3 3 3 个输入变量, 1 1 1 个输出变量。设 3 3 3 个输入变量分别为 A A A、 B B B、 C C C,其中 A A A 表示主裁判输入: 1 1 1 表示同意, 0 0 0 表示不同意;设输出变量为 F F F,输出: 1 1 1 表示通过, 0 0 0 表示不通过。 (2)列出真值表 (5)画出逻辑电路图 F = A B + A C F=AB+AC F=AB+AC 同一个电路可用不同的逻辑门来实现,需要根据所用的逻辑门对化简后的逻辑函数进行变形处理。 除了基本逻辑门电路之外,常用的逻辑门电路有与非门、或非门、与或非门等。 方法1:用与门、或门实现: 方法2:用与非门实现:与非-与非表达式:
F
=
A
B
+
A
C
=
A
B
+
A
C
‾
‾
=
A
B
‾
⋅
A
C
‾
‾
F=AB+AC = \overline{ \overline { AB +AC}} = \overline {\overline {AB} \cdot \overline {AC}}
F=AB+AC=AB+AC=AB⋅AC 方法3:用或非门实现:
F
=
A
B
+
A
C
=
A
B
+
A
C
‾
‾
=
A
(
B
+
C
)
‾
‾
=
A
‾
+
B
+
C
‾
‾
=
A
+
A
‾
+
B
+
C
‾
‾
F = AB+AC = \overline{ \overline { AB +AC}} = \overline{ \overline { A(B +C)}} = \overline{ \overline A + \overline { B +C}} = \overline{ \overline {A+A} + \overline{ B +C}}
F=AB+AC=AB+AC=A(B+C)=A+B+C=A+A+B+C 通过卡诺图求或非 - 或非表达式: 例2:设计一个可以实现 4 4 4 位 格雷码和 4 4 4 位二进制编码的相互转换电路,有一个控制端 S S S:当 S = 1 S=1 S=1 时,可以将输入的 4 4 4 位格雷码转换成 4 4 4 位二进制编码;当 S = 0 S=0 S=0 时,实现将输入的 4 4 4 位二进制编码转换成 4 4 4 位格雷码。 解 (1)确定输入输出:根据题意,有 5 5 5 个输入变量, 4 4 4 个输出变量。 5 5 5 个输入变量分别为控制变量 S S S 和 4 4 4 位输入码(格雷码或者 4 4 4 位二进制码);输出变量为 4 4 4 位输出码( 4 4 4 位二进制码或者格雷码)。 (2)列出真值表
S
=
0
S=0
S=0 时真值表:
S
=
0
S=0
S=0 时真值表:
S
=
0
S=0
S=0 时真值表:
S
=
0
S=0
S=0 时真值表:
S
=
1
S=1
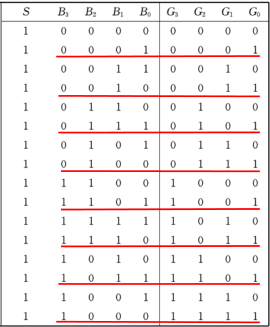
S=1 时真值表:
S
=
1
S=1
S=1 时真值表:
S
=
1
S=1
S=1 时真值表:
S
=
1
S=1
S=1 时 真值表 (4)画出逻辑电路图 1.试写出习题图所示组合逻辑电路的输出逻辑表达式,并画出与之功能相同的简化逻辑电路。 解:可得 F = ( A B + A + B ‾ ‾ ) ⋅ C ‾ + ( A B + A + B ‾ ) ⋅ C ‾ = ( A B + A + B ‾ ) ⊙ C ‾ = ( A B + A + B ‾ ) ‾ ⊕ C ‾ = ( A ‾ + B ‾ ) ⋅ ( A + B ) ⊕ C ‾ = ( A ‾ B + A B ‾ ) ⊕ C ‾ = A ⊕ B ⊕ C ‾ \begin{aligned} F&= \overline {(\overline {AB + \overline {A+B}}) \cdot \overline C +\ (AB+\overline {A+B}) \cdot C}\\ &= \overline {(AB + \overline {A+B})\odot C}\\ &= \overline { (AB+\overline {A+B})} \oplus \overline C\\ &= (\overline A+\overline B) \cdot (A+B) \oplus \overline C\\ &=(\overline AB+A\overline B) \oplus \overline C\\ &= A \oplus B \oplus \overline C \end{aligned} F=(AB+A+B)⋅C+ (AB+A+B)⋅C=(AB+A+B)⊙C=(AB+A+B)⊕C=(A+B)⋅(A+B)⊕C=(AB+AB)⊕C=A⊕B⊕C 列出真值表如下: ABC A ⊕ B ⊕ C ‾ A\oplus B\oplus \overline C A⊕B⊕C00010010010001111000101111011110从真值表可以看出,这个电路是判断三个输入中
0
0
0 信号是否为奇数个,是则结果为
1
1
1,否则结果为
0
0
0 。可以用非门和异或门进行电路简化: 3.设 A , B , C A,B,C A,B,C 为某保密锁的三个按键,当 A A A 被单独按下时,锁既不打开也不报警,只有当 A , B , C A,B,C A,B,C,或者 A , B A,B A,B,或者 A , C A,C A,C 分别同时按下时,锁才能被打开;当不符合上述组合状态时,将发出报警信息,试用门电路实现此保密锁电路。 解:设三个按键 A , B , C A,B,C A,B,C 为输入量,按下为 1 1 1,不按下为 0 0 0;设 Y , G Y,G Y,G 分别为打开信号和报警信号,打开为 1 1 1,不打开为 0 0 0,报警为 1 1 1,不报警为 0 0 0。 真值表如下: ABCYG0000000101010010110110000101101101011110根据真值表写表达式并化简:
F
=
A
B
‾
C
+
A
B
C
‾
+
A
B
C
=
A
B
‾
C
+
A
B
=
A
(
B
‾
C
+
B
)
=
A
(
B
+
B
‾
)
⋅
(
B
+
C
)
=
A
B
+
A
C
G
=
A
‾
B
‾
C
+
A
‾
B
C
‾
+
A
‾
B
C
=
A
‾
B
‾
C
+
A
‾
B
=
A
‾
(
B
‾
C
+
B
)
=
A
‾
(
B
+
B
‾
)
⋅
(
B
+
C
)
=
A
‾
B
+
A
‾
C
\begin{aligned} F &= A\overline BC + AB\overline C + ABC\\ &= A\overline BC + AB\\ &=A(\overline BC+B)\\ &= A(B +\overline B) \cdot (B + C)\\ &= AB + AC\\ G &= \overline A\ \overline BC + \overline AB\overline C + \overline A BC\\ &=\overline A\ \overline BC +\overline AB\\ &= \overline A(\overline BC+B)\\ &= \overline A(B +\overline B) \cdot (B + C)\\ &= \overline AB + \overline AC \end{aligned}
FG=ABC+ABC+ABC=ABC+AB=A(BC+B)=A(B+B)⋅(B+C)=AB+AC=A BC+ABC+ABC=A BC+AB=A(BC+B)=A(B+B)⋅(B+C)=AB+AC 用与门、或门和非门实现如下: |
【本文地址】
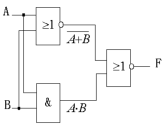 解 : 该电路为二级组合电路。 (1) 写出电路的逻辑表达式
F
=
A
+
B
‾
+
A
B
‾
=
(
A
+
B
)
(
A
‾
+
B
‾
)
=
A
‾
B
+
A
B
‾
\begin{aligned} F &= \overline {\overline {A+B} + AB}\\ &= (A+B)(\overline A + \overline B)\\ &= \overline AB + A\overline B \end{aligned}
F=A+B+AB=(A+B)(A+B)=AB+AB (2) 描述电路的逻辑功能:该函数表达式比较简单,不用列真值表,由表达式可知此电路是一个异或电路 。
解 : 该电路为二级组合电路。 (1) 写出电路的逻辑表达式
F
=
A
+
B
‾
+
A
B
‾
=
(
A
+
B
)
(
A
‾
+
B
‾
)
=
A
‾
B
+
A
B
‾
\begin{aligned} F &= \overline {\overline {A+B} + AB}\\ &= (A+B)(\overline A + \overline B)\\ &= \overline AB + A\overline B \end{aligned}
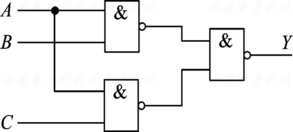
F=A+B+AB=(A+B)(A+B)=AB+AB (2) 描述电路的逻辑功能:该函数表达式比较简单,不用列真值表,由表达式可知此电路是一个异或电路 。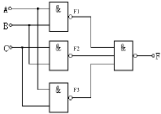 (1) 写出电路的逻辑表达式
F
=
F
1
⋅
F
2
⋅
F
3
‾
=
A
B
‾
⋅
B
C
‾
⋅
A
C
‾
‾
=
A
B
+
B
C
‾
+
A
C
\begin{aligned} F&=\overline {F_1 \cdot F_2 \cdot F_3}\\ &=\overline {\overline {AB} \cdot \overline {BC} \cdot \overline {AC}}\\ &= AB +B\overline C+AC \end{aligned}
F=F1⋅F2⋅F3=AB⋅BC⋅AC=AB+BC+AC (2) 列真值表
(1) 写出电路的逻辑表达式
F
=
F
1
⋅
F
2
⋅
F
3
‾
=
A
B
‾
⋅
B
C
‾
⋅
A
C
‾
‾
=
A
B
+
B
C
‾
+
A
C
\begin{aligned} F&=\overline {F_1 \cdot F_2 \cdot F_3}\\ &=\overline {\overline {AB} \cdot \overline {BC} \cdot \overline {AC}}\\ &= AB +B\overline C+AC \end{aligned}
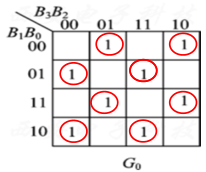
F=F1⋅F2⋅F3=AB⋅BC⋅AC=AB+BC+AC (2) 列真值表  (3) 描述电路的逻辑功能:
(3) 描述电路的逻辑功能: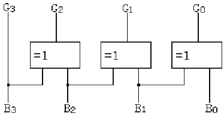 (1) 写出电路的逻辑表达式
G
3
=
B
3
G
2
=
B
3
⊕
B
2
G
1
=
B
2
⊕
B
1
G
0
=
B
1
⊕
B
0
\begin{aligned} G_3 &= B_3\\ G_2 &= B_3 \oplus B_2\\ G_1 &= B_2 \oplus B_1\\ G_0 &= B_1 \oplus B_0 \end{aligned}
G3G2G1G0=B3=B3⊕B2=B2⊕B1=B1⊕B0 (2) 列写真值表
(1) 写出电路的逻辑表达式
G
3
=
B
3
G
2
=
B
3
⊕
B
2
G
1
=
B
2
⊕
B
1
G
0
=
B
1
⊕
B
0
\begin{aligned} G_3 &= B_3\\ G_2 &= B_3 \oplus B_2\\ G_1 &= B_2 \oplus B_1\\ G_0 &= B_1 \oplus B_0 \end{aligned}
G3G2G1G0=B3=B3⊕B2=B2⊕B1=B1⊕B0 (2) 列写真值表  (3) 描述电路的逻辑功能:自然二进制码到格雷码的转换电路。
(3) 描述电路的逻辑功能:自然二进制码到格雷码的转换电路。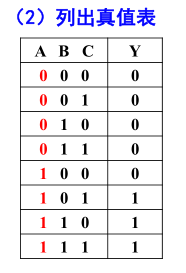 (3)由真值表写出表达式
F
=
A
B
‾
C
+
A
B
C
‾
+
A
B
C
F = A\overline BC + AB\overline C +ABC
F=ABC+ABC+ABC (4)化简表达式
F
=
A
B
‾
C
+
A
B
C
‾
+
A
B
C
=
A
B
‾
C
+
A
B
(
C
+
C
‾
)
=
A
B
‾
C
+
A
B
=
A
(
B
+
B
‾
C
)
=
A
(
B
+
C
)
=
A
B
+
A
C
\begin{aligned} F &= A\overline BC + AB\overline C +ABC\\ &=A\overline BC + AB(C +\overline C)\\ &= A\overline BC+ AB\\ &= A(B+\overline BC)\\ &= A(B+C)\\&= AB +AC \end{aligned}
F=ABC+ABC+ABC=ABC+AB(C+C)=ABC+AB=A(B+BC)=A(B+C)=AB+AC
(3)由真值表写出表达式
F
=
A
B
‾
C
+
A
B
C
‾
+
A
B
C
F = A\overline BC + AB\overline C +ABC
F=ABC+ABC+ABC (4)化简表达式
F
=
A
B
‾
C
+
A
B
C
‾
+
A
B
C
=
A
B
‾
C
+
A
B
(
C
+
C
‾
)
=
A
B
‾
C
+
A
B
=
A
(
B
+
B
‾
C
)
=
A
(
B
+
C
)
=
A
B
+
A
C
\begin{aligned} F &= A\overline BC + AB\overline C +ABC\\ &=A\overline BC + AB(C +\overline C)\\ &= A\overline BC+ AB\\ &= A(B+\overline BC)\\ &= A(B+C)\\&= AB +AC \end{aligned}
F=ABC+ABC+ABC=ABC+AB(C+C)=ABC+AB=A(B+BC)=A(B+C)=AB+AC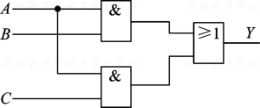
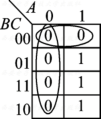 圈
0
0
0 ,得到或-与表达式
F
=
(
B
+
C
)
A
F=(B+C)A
F=(B+C)A;将或-与表达式两次求非
F
=
(
B
+
C
)
A
‾
‾
F = \overline {\overline {(B+C)A}}
F=(B+C)A;通过公式法求或非-或非表达式
F
=
B
+
C
‾
+
A
‾
‾
F=\overline {\overline{B+C}+\overline A}
F=B+C+A。
圈
0
0
0 ,得到或-与表达式
F
=
(
B
+
C
)
A
F=(B+C)A
F=(B+C)A;将或-与表达式两次求非
F
=
(
B
+
C
)
A
‾
‾
F = \overline {\overline {(B+C)A}}
F=(B+C)A;通过公式法求或非-或非表达式
F
=
B
+
C
‾
+
A
‾
‾
F=\overline {\overline{B+C}+\overline A}
F=B+C+A。 
 (3)根据卡诺图写函数表达式 本题涉及
5
5
5 个变量,采用卡诺图化简逻辑表达式比较麻烦。为了减少变量个数,可以分为
S
=
0
S=0
S=0 和
S
=
1
S=1
S=1 两种情况来处理。
(3)根据卡诺图写函数表达式 本题涉及
5
5
5 个变量,采用卡诺图化简逻辑表达式比较麻烦。为了减少变量个数,可以分为
S
=
0
S=0
S=0 和
S
=
1
S=1
S=1 两种情况来处理。
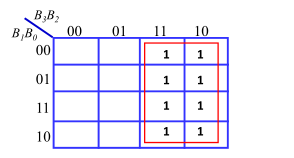 可以得到:
G
3
=
B
3
G_3 = B_3
G3=B3;
可以得到:
G
3
=
B
3
G_3 = B_3
G3=B3;
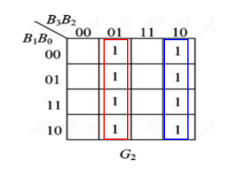 可以得到:
G
2
=
B
3
‾
B
2
+
B
3
B
2
‾
=
B
3
⊕
B
2
G_2 = \overline {B_3} B_2 + B_3 \overline{B_2} = B_3 \oplus B_2
G2=B3B2+B3B2=B3⊕B2。
可以得到:
G
2
=
B
3
‾
B
2
+
B
3
B
2
‾
=
B
3
⊕
B
2
G_2 = \overline {B_3} B_2 + B_3 \overline{B_2} = B_3 \oplus B_2
G2=B3B2+B3B2=B3⊕B2。
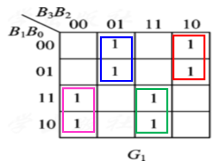
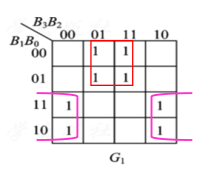 可以得到
G
1
=
B
2
‾
B
1
+
B
2
B
1
‾
=
B
2
⊕
B
1
G_1 = \overline {B_2}B_1 + B_2\overline{B_1} = B_2\oplus B_1
G1=B2B1+B2B1=B2⊕B1。
可以得到
G
1
=
B
2
‾
B
1
+
B
2
B
1
‾
=
B
2
⊕
B
1
G_1 = \overline {B_2}B_1 + B_2\overline{B_1} = B_2\oplus B_1
G1=B2B1+B2B1=B2⊕B1。
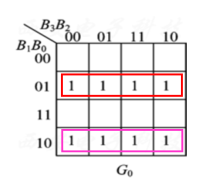 可得:
G
0
=
B
‾
1
B
0
+
B
1
B
‾
0
=
B
1
⊕
B
0
G_0 = \overline B_1B_0 + B_1\overline B_0 = B_1 \oplus B_0
G0=B1B0+B1B0=B1⊕B0 。
可得:
G
0
=
B
‾
1
B
0
+
B
1
B
‾
0
=
B
1
⊕
B
0
G_0 = \overline B_1B_0 + B_1\overline B_0 = B_1 \oplus B_0
G0=B1B0+B1B0=B1⊕B0 。
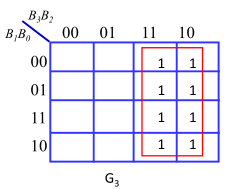 则
G
3
=
B
3
G_3 = B_3
G3=B3 。
则
G
3
=
B
3
G_3 = B_3
G3=B3 。
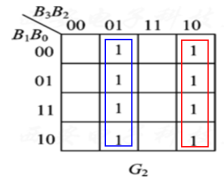 G
2
=
B
3
‾
B
2
+
B
3
B
2
‾
=
B
3
⊕
B
2
G_2 = \overline {B_3} B_2 + B_3 \overline{B_2} = B_3 \oplus B_2
G2=B3B2+B3B2=B3⊕B2。
G
2
=
B
3
‾
B
2
+
B
3
B
2
‾
=
B
3
⊕
B
2
G_2 = \overline {B_3} B_2 + B_3 \overline{B_2} = B_3 \oplus B_2
G2=B3B2+B3B2=B3⊕B2。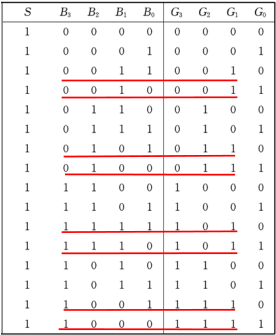
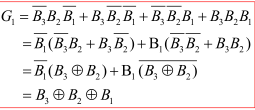
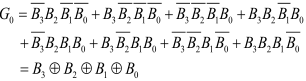

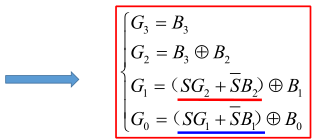

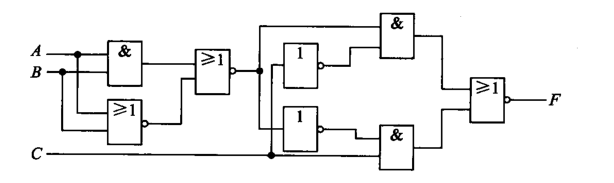
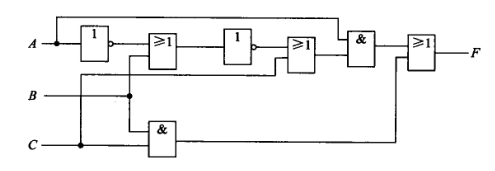 解:输出逻辑表达式如下:
F
=
(
A
‾
+
B
‾
+
C
)
⋅
A
+
B
C
=
(
A
⋅
B
‾
+
C
)
⋅
A
+
B
C
=
A
B
‾
+
A
C
+
B
C
=
A
B
‾
+
B
C
+
A
(
B
+
B
‾
)
C
=
A
B
‾
+
B
C
+
A
B
C
+
A
B
‾
C
=
A
B
‾
+
B
C
\begin{aligned} F &= (\overline {\overline A+B} + C) \cdot A + BC \\ &= (A\cdot \overline B + C) \cdot A + BC\\ &= A\overline B + AC +BC\\ &= A\overline B + BC + A(B + \overline B)C\\ &= A\overline B +BC + ABC + A\overline BC\\ &= A\overline B + BC \end{aligned}
F=(A+B+C)⋅A+BC=(A⋅B+C)⋅A+BC=AB+AC+BC=AB+BC+A(B+B)C=AB+BC+ABC+ABC=AB+BC 与之功能相同的简化逻辑电路:
解:输出逻辑表达式如下:
F
=
(
A
‾
+
B
‾
+
C
)
⋅
A
+
B
C
=
(
A
⋅
B
‾
+
C
)
⋅
A
+
B
C
=
A
B
‾
+
A
C
+
B
C
=
A
B
‾
+
B
C
+
A
(
B
+
B
‾
)
C
=
A
B
‾
+
B
C
+
A
B
C
+
A
B
‾
C
=
A
B
‾
+
B
C
\begin{aligned} F &= (\overline {\overline A+B} + C) \cdot A + BC \\ &= (A\cdot \overline B + C) \cdot A + BC\\ &= A\overline B + AC +BC\\ &= A\overline B + BC + A(B + \overline B)C\\ &= A\overline B +BC + ABC + A\overline BC\\ &= A\overline B + BC \end{aligned}
F=(A+B+C)⋅A+BC=(A⋅B+C)⋅A+BC=AB+AC+BC=AB+BC+A(B+B)C=AB+BC+ABC+ABC=AB+BC 与之功能相同的简化逻辑电路:  2.试分析习题图所示组合逻辑电路的功能,并用数量最少、品种最少的门电路实现。
2.试分析习题图所示组合逻辑电路的功能,并用数量最少、品种最少的门电路实现。