| 专题 直线与圆的最值问题 | 您所在的位置:网站首页 › 绝对值最值问题视频讲解 › 专题 直线与圆的最值问题 |
专题 直线与圆的最值问题
|
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义! \(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\) 选择性必修第一册同步提高,难度4颗星! 模块导图 知识剖析
1 最值模型
知识剖析
1 最值模型
(1) 三点共线模型(三角形三边的关系)
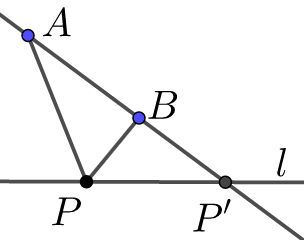
\((i)\)点\(A\)、\(B\)在直线\(l\)同侧,点\(P\)在直线\(l\)上,则\((A P+B P)_{\min }=A B^{\prime}\)(当点\(A\)、\(P\)、\(B'\)共线时取到),点\(B'\)是点\(B\)关于直线l的对称点.
\((ii)\)点\(A\)、\(B\)在直线\(l\)同侧,点\(P\)在直线\(l\)上,则\(| A P-\left.B P\right|_{\max }=A B\)(当点\(A\)、\(P\)、\(B\)共线时取到).
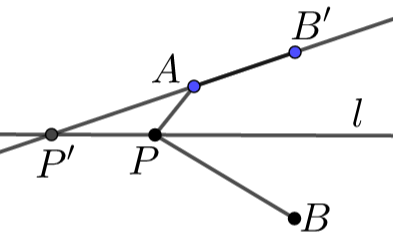
\((iii)\)点\(A\)、\(B\)在直线\(l\)异侧,点\(P\)在直线\(l\)上,则\(|A P-B P|_{\max }=A B^{\prime}\)(当点\(A\)、\(P\)、\(B\)共线时取到),点\(B'\)是点\(B\)关于直线\(l\)的对称点.
(2) 某点\(M\)到圆\(⊙O\)上点\(N\)的距离
\((i)\)若点\(M\)在圆内,则\(M N_{\min }=M N_{1}=r-O M\),\(M N_{\max }=M N_{2}=r+O M\);
\((ii)\)若点\(M\)在圆外,则\(M N_{\min }=M N_{1}=O M-r\),\(M N_{\max }=M N_{2}=r+O M\);
(3) 圆上一点到圆外一定直线的距离最值
若直线\(l\)与圆\(⊙O\)相离,圆上一点\(P\)到直线\(l\)的距离为\(PE\),\(d\)为圆心\(O\)到直线l的距离,\(r\)为圆半径,则\(P E_{\min }=P_{1} F=d-r\),\(P E_{\max }=P_{2} F=d+r\).
2 圆的参数方程 圆的标准方程\((x-a)^2+(y-b)^2=r^2\),圆心为\((a ,b)\),半径为\(r\),
它对应的圆的参数方程:\(\left\{\begin{array}{l}
x=r \cos \theta+a \\
y=r \sin \theta+b
\end{array}\right.\)(\(θ\)是参数).
【典题1】\(P\)是直线\(L:3x-y-1=0\)上一点,求
\((1)\)\(P\)到\(A(4 ,1)\)和\(B(0 ,4)\)的距离之差的最大值;
\((2)\)\(P\)到\(A(4 ,1)\)和\(C(3 ,4)\)的距离之和的最小值.
【解析】(1)显然\(A\)、\(B\)位于直线\(L\)两侧,
作\(B\)关于直线\(L\)的对称点\(B'\),连接\(B'A\),\(B'A\)所在直线与直线\(L\)交点为\(P_1\),
此时\(PA-PB\)的差值最大,最大值就是\(B'A\),
设\(B\)点关于\(L\)对称点\(B'(a ,b)\),
则\(\dfrac{b-4}{a-0} \times 3=-1\),\(3 a-(b+4)-2=0\),
\({\color{Red}{(k_{B B'} \cdot k_{l}=-1, BB'中点在l上) }}\)
得\(a=3\),\(b=3\),\(∴B'(3 ,3)\),
\(\therefore B^{\prime} A=\sqrt{(4-3)^{2}+(1-3)^{2}}=\sqrt{5}\),
即\(P\)到\(A(4 ,1)\)和\(B(0 ,4)\)的距离之差最大值为\(\sqrt{5}\);
(2)显然\(A\)、\(C\)位于直线\(L\)同侧, \({\color{Red}{(将军饮马模型) }}\)
作点\(C\)关于直线\(L\)对称点\(C'\),连接\(C'A\),\(C'A\)所在直线与直线\(L\)的交点为\(P_2\), 此时\(PA+PB\)之和最小,最小值为\(C'A\), 设\(C\)关于\(l\)的对称点为\(C'(m ,n)\), 可得\(\dfrac{n-4}{m-3}=-\dfrac{1}{3}\),\(\dfrac{3(m+3)}{2}-\dfrac{n+4}{2}-1=0\), 解得\(m=\dfrac{3}{5}\),\(n=\dfrac{24}{5}\),即\(C'\)的坐标为\(\left(\dfrac{3}{5}, \dfrac{24}{5}\right)\), \(\therefore C^{\prime} A=\sqrt{\left(\dfrac{3}{5}-4\right)^{2}+\left(\dfrac{24}{5}-1\right)^{2}}=\sqrt{26}\), 即\(P\)到\(A(4 ,1)\)和\(C(3 ,4)\)的距离之和最小值为\(\sqrt{26}\). 【点拨】三点共线模型,主要是利用三角形三边共线(任意两边之和大于第三边,任意两边之差小于第三边),当三点共线时取到最值,熟悉模型快速判断模型是关键. 情况2 斜率型最值【典题1】如果实数\(x\),\(y\)满足条件:\((x-2)^2+y^2=3\),那么\(\dfrac{y}{x}\)的最大值是\(\underline{\quad \quad}\) .
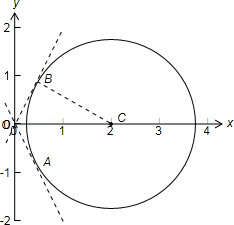
【解析】满足方程\((x-2)^2+y^2=3\)的图形是个圆,
\(\dfrac{y}{x}=\dfrac{y-0}{x-0}\)表示圆上动点\((x ,y)\)与原点\(O(0 ,0)\)连线的斜率, 由图可得动点与\(B\)重合时,此时\(OB\)与圆相切,\(\dfrac{y}{x}\)取最大值, 连接\(BC\),在\(Rt△OBC\)中,\(B C=\sqrt{3}\),\(OC=2,\) \(\because \sin \angle B O C=\dfrac{B C}{O C}=\dfrac{\sqrt{3}}{2}\),\(\therefore \angle B O C=60^{\circ}\), 此时\(\dfrac{y}{x}=\tan 60^{\circ}=\sqrt{3}\). 【点拨】 ① 本题很好地体现了数形结合,把代数问题转化为几何问题处理; ② 直线斜率公式是\(k=\dfrac{y_{1}-y_{2}}{x_{1}-x_{2}}\),对于形如\(\dfrac{y-a}{x-b}\)可理解为点\((x ,y)\)与点\((a ,b)\)之间的斜率,其最值问题可化为几何中斜率的最值问题. 情况3 两点距离型最值【典题1】已知点\(M(a ,b)\)在直线\(l:3x+4y=25\)上,则\(a^2+b^2\)的最小值为\(\underline{\quad \quad}\). 【解析】\(\because \sqrt{a^{2}+b^{2}}=\sqrt{(a-0)^{2}+(b-0)^{2}}\)的几何意义是点\(O(0 ,0)\)到点\(M\)的距离, \({\color{Red}{(而a^2+b^2是其距离的平方) }}\) 又点\(M\)在直线\(l\)上, \(\therefore \sqrt{a^{2}+b^{2}}\)的最小值为点\(O\)到直线l的距离\(d\), \({\color{Red}{ (垂线段最短) }}\) 又\(d=\dfrac{25}{\sqrt{3^{2}+4^{2}}}=5\),\(\therefore\left(\sqrt{a^{2}+b^{2}}\right)_{\min }=5,\), 则\(\left(a^{2}+b^{2}\right)_{\min }=25\). 【点拨】 ① 本题解法中很好利用两点距离公式\(A B=\sqrt{\left(x_{A}-x_{B}\right)^{2}+\left(y_{A}-y_{B}\right)^{2}}\). (以下\(x\)、\(y\)是变量,它们满足某些限制条件,\(a\),\(b\)是常数) 求形如\(\sqrt{(x-a)^{2}+(y-b)^{2}}\)或\((x-a)^2+(y-b)^2\)式子的最值,可理解为动点\((x ,y)与\)定点\((a ,b)\)的距离最值问题. ② 本题用代数的方法求解与之比较下,体会下两种方法的不同. 【典题2】 已知点\(P\),\(Q\)分别在直线\(l_1:x+y+2=0\)与直线\(l_2:x+y-1=0\)上,且\(PQ⊥l_1\),点\(A(-3 ,-3)\),\(B\left(\dfrac{3}{2}, \dfrac{1}{2}\right)\),则\(|AP|+|PQ|+|QB|\)的最小值为\(\underline{\quad \quad}\) .
【解析】
\({\color{Red}{方法1 }}\)由平行线距离公式得\(|P Q|=\dfrac{3}{\sqrt{2}}=\dfrac{3 \sqrt{2}}{2}\),
设\(P(a ,-a-2)\),
由图可知\(k_{P Q}=1\),即倾斜角为\(\dfrac{\pi}{4}\),
\(\therefore \sqrt{2}\left(x_{Q}-x_{P}\right)=|P Q|=\dfrac{3 \sqrt{2}}{2} \Rightarrow x_{Q}=a+\dfrac{3}{2}\),
则\(Q\left(a+\dfrac{3}{2},-a-\dfrac{1}{2}\right)\),
所以\(|AP|+|PQ|+|QB|\)
\(=\sqrt{(a+3)^{2}+(-a+1)^{2}}+\sqrt{a^{2}+(-a-1)^{2}}+\dfrac{3 \sqrt{2}}{2}\)
\(=\sqrt{(a+3)^{2}+(a-1)^{2}}+\sqrt{a^{2}+(a+1)^{2}}+\dfrac{3 \sqrt{2}}{2}\)
\({\color{Red}{(利用两点距离公式把所求的用a表示处理,此时若想用函数最值的方法求解较难) }}\)
设点\(M(a ,a)\),\(C(1 ,-3)\),\(D(-1 ,0)\),如图:
则有\(\sqrt{(a+3)^{2}+(a-1)^{2}}+\sqrt{a^{2}+(a+1)^{2}}\)
\(=|M C|+|M D| \geq|C D|=\sqrt{13}\)
(即当\(D\)、\(M\)、\(C\)三点共线时等号成立),
\({\color{Red}{ (此时巧妙的用两点距离公式把式子\sqrt{(a+3)^{2}+(a-1)^{2}}+\sqrt{a^{2}+(a+1)^{2}}为一动点到两定点的距离之和,}}\)
\({\color{Red}{达到了几何化的目的)}}\)
综上,\(|A P|+|P Q|+|Q B| \geq \sqrt{13}+\dfrac{3 \sqrt{2}}{2}\).
\({\color{Red}{方法2 }}\)
\({\color{Red}{(把点A向\overrightarrow{P Q}方向移动|PQ|长度单位到A_1,则问题“|AP|+|PQ|+|QB|的最小值”转化为}}\)
\({\color{Red}{求在l_2上找点Q使得A_1 Q+BQ最小,显然是A_1 B.) }}\)
如图,如方法\(1\)易得\(k_{P Q}=1\),\(P Q=\dfrac{3 \sqrt{2}}{2}\),
【典题1】已知\(x\)、\(y\)满足\((x-1)^2+y^2=1\),则\(S=x^2+y^2+2x-2y+2\)的最小值是\(\underline{\quad \quad}\) .
【解析】方程\((x-1)^2+y^2=1\)可理解为圆心\(M(1 ,0)\),半径\(r=1\)的圆,
而\(S=x^2+y^2+2x-2y+2= (x+1)^2+(y-1)^2\)
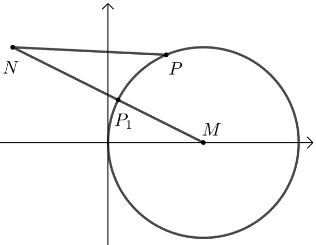
可理解为点\(P(x ,y)\)到点\(N(-1 ,1)\)的距离平方, 则问题转化为圆外一定点\(N(-1 ,1)\)到圆上点\(P(x ,y)\)距离最小值, 点\(N(-1 ,1)\)到圆\((x-1)^2+y^2=1\)上点的最短距离为 \(P_{1} N=M N-r=\sqrt{(1+1)^{2}+1}-1=\sqrt{5}-1\), 则\(S_{\min }=(\sqrt{5}-1)^{2}=6-2 \sqrt{5}\). 【点拨】 ① 本题把方程\((x-1)^2+y^2=1\)理解为圆,\(S= (x+1)^2+(y-1)^2\)理解为两点距离的平方; ② 注意点\(N\)在圆内还是圆外. 【典题2】已知点\(P(7 ,3)\),圆\(M:x^2+y^2-2x-10y+25=0\),点\(Q\)为在圆\(M\)上一点,点\(S\)在\(x\)轴上,则\(|SP|+|SQ|\)的最小值为\(\underline{\quad \quad}\) .
【解析】由题意知,圆的方程化为\((x-1)^{2}+(y-5)^{2}=1\),圆心\(M(1 ,5)\),半径为\(1\);
\({\color{Red}{ (本题是双动点问题,它们之间没有联系,可采取先“固定”一动点Q的方法)}}\)
分两步:
\({\color{Red}{第一步 }}\) 假设圆上点\(Q\)不动,此时点\(S\)在\(x\)轴上运动,
求\(|SP|+|SQ|\)的最小值,这就是“将军饮马问题”,
如图所示,作点\(P(7 ,3)\)关于\(x\)轴的对称点\(P'(7 ,-3)\);
此时\(|SP|+|SQ|\)的最小值为\(|P'Q|\)
(即说不管点\(Q\)在什么位置,最小值都是\(|P'Q|\)),
\({\color{Red}{第二步 }}\)再把动点\(Q\)动起来,
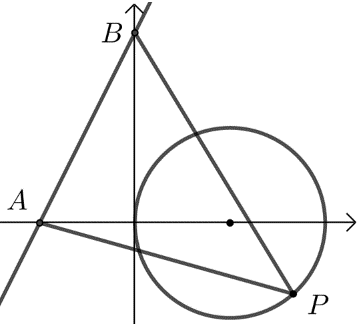
此时是圆外一定点\(P'\)到圆上一点的距离最值问题了, 显然\(\left|P^{\prime} Q\right|_{\min }=\left|P^{\prime} Q^{\prime}\right|\) \(=\left|P^{\prime} M\right|-r=\left|P^{\prime} M\right|-1\) \(=\sqrt{(1-7)^{2}+(5+3)^{2}}-1=9\), 故\(|SP|+|SQ|\)的最小值为\(9\). 【点拨】两动点\((A,B)\)问题,若两动点没内在联系的,可先“固定”一动点\(A\),思考点\(B\)运动时的最值,确定后再“释放”动点\(A\),求出最终的最值. 情况5 圆上一点到圆外一定直线的距离最值【典题1】已知两点\(A(-1,0)\)、\(B(0,2)\),若点\(P\)是圆\((x-1)^2+y^2=1\)上的动点,则\(△ABP\)面积的最大值和最小值之和为\(\underline{\quad \quad}\).
【解析】
\({\color{Red}{(S_{\triangle A B P}以AB为底,求其最值,即求点P到直线AB的距离最值) }}\)
由两点\(A(-1,0)\)、\(B(0,2)\), \(\therefore|A B|=\sqrt{(-1)^{2}+2^{2}}=\sqrt{5}\), 直线\(AB\)的方程为\(\dfrac{x}{-1}+\dfrac{y}{2}=1\),即\(2x-y+2=0\), 由圆\((x-1)^2+y^2=1\)可得圆心\(C(1,0)\),半径\(r=1\), 则圆心\(C\)到直线\(AB\)的距离\(d=\dfrac{|2-0+2|}{\sqrt{5}}=\dfrac{4}{\sqrt{5}}\), \(∵\)点\(P\)是圆\((x-1)^2+y^2=1\)上的动点, \(∴\)点\(P\)到直线\(AB\)的最大距离\(d_{\max }=d+r\);点\(P\)到直线\(AB\)的最小距离\(d_{\min }=d-r\). \(∴△ABP\)面积的最大值和最小值之和等于 \(\dfrac{1}{2}|A B| \cdot d_{\max }+\dfrac{1}{2}|A B| d_{\min }=\dfrac{1}{2}|A B| \cdot\left(d_{\max }+d_{\min }\right)=\dfrac{1}{2} \times \sqrt{5} \cdot \dfrac{8}{\sqrt{5}}=4\). 【点拨】圆上一点\(P\)到圆外一直线\(l\)距离\(d\)与圆心\(O\)到直线\(l\)的距离\(d_1\)和圆的半径\(r\)有关,即\(d_{\min }=d_{1}-r\),\(d_{\max }=d_{1}+r\). 巩固练习1(★★)已知\(x^2+y^2=1\),则\(\dfrac{y}{x+2}\)的取值范围是\(\underline{\quad \quad}\). 2(★★)已知点\(P(x ,y)\)在圆\(x^2+y^2=1\)上,则\(\sqrt{(x-1)^{2}+(y-1)^{2}}\)的最大值为\(\underline{\quad \quad}\). 3(★★)已知圆\(x^2+(y-2)^2=1\)上一动点\(A\),定点\(B(6 ,1)\);\(x\)轴上一点\(W\),则\(|AW|+|BW|\)的最小值等于\(\underline{\quad \quad}\). 4(★★)已知两个同心圆的半径分别为\(3\)和\(4\),圆心为\(O\).点\(P\)、\(Q\)分别是大圆、小圆上的任意一点,线段\(PQ\)的中垂线为\(l\).若光线从点\(O\)射出,经直线\(l\)(入射光线与直线\(l\)的公共点为\(A\))反射后经过点\(Q\),则\(|OA|-|AQ|\)的取值范围是\(\underline{\quad \quad}\). 5(★★)已知点\(A(-2 ,0)\),\(B(0 ,2)\),若点\(P\)在圆\((x-3)^{2}+(y+1)^{2}=2\)上运动,则\(△ABP\)面积的最小值为\(\underline{\quad \quad}\). 6(★★)过动点\(P\)作圆:\((x-3)^2+(y-4)^2=1\)的切线\(PQ\),其中\(Q\)为切点,若\(|PQ|=|PO|\)(\(O\)为坐标原点),则\(|PQ|\)的最小值是\(\underline{\quad \quad}\). 7(★★)已知直线\(l:x-y+4=0\)与\(x\)轴相交于点\(A\),过直线\(l\)上的动点\(P\)作圆\(x^2+y^2=4\)的两条切线,切点分别为\(C\),\(D\)两点,记\(M\)是\(CD\)的中点,则\(|AM|\)的最小值为\(\underline{\quad \quad}\). 8(★★)已知圆\((x-a)^2+(y-b)^2=1\)经过原点,则圆上的点到直线\(y=x+2\)距离的最大值为\(\underline{\quad \quad}\). 9(★★★)如图,设圆\(C_{1}:(x-5)^{2}+(y+2)^{2}=4\),圆\(C_{2}:(x-7)^{2}+(y+1)^{2}=25\),点\(A\)、\(B\)分别是圆\(C_1\),\(C_2\)上的动点,\(P\)为直线\(y=x\)上的动点,则\(|PA|+|PB|\)的最小值为\(\underline{\quad \quad}\).
参考答案 1.\(\left[-\dfrac{\sqrt{3}}{3}, \dfrac{\sqrt{3}}{3}\right]\) 2.\(\sqrt{2}+1\) 3.\(3 \sqrt{5}-1\) 4.\([-4 ,3\)] 5.\(4\) 6.\(\dfrac{12}{5}\) 7.\(2 \sqrt{2}\) 8.\(\sqrt{2}+2\) 9.\(3 \sqrt{13}-7\) 【题型二】代数法处理最值问题【典题1】已知圆\(C\)的圆心在直线\(x-2y=0\)上,且经过点\(M(0 ,-1)\),\(N(1 ,6)\). (1)求圆\(C\)的方程; (2)已知点\(A(1 ,1)\),\(B(7 ,4)\),若\(P\)为圆\(C\)上的一动点,求\(|PA|^2+|PB|^2\)的取值范围. 【解析】(1)设圆心\(C(a ,b)\),则\(a-2b=0\), 由\(|MC|=|NC|\)得\(\sqrt{(a-0)^{2}+(b+1)^{2}}=\sqrt{(a-1)^{2}+(b-6)^{2}} \Rightarrow a+7 b=18\), 解得\(b=2\),\(a=4\), \(∴\)圆的半径\(r=MC=5\), 所以圆\(C\)的方程为\((x-4)^2+(y-2)^2=25\). (2) \({\color{Red}{方法1 }}\) 设\(P(x ,y)\), \({\color{Red}{(设元,引入变量x, y) }}\) 则\((x-4)^2+(y-2)^2=25\),即\(x^2+y^2=5+8x+4y\) 则\(|PA|^2+|PB|^2\) \({\color{Red}{(利用两点距离公式用x, y表示|PA|^2+|PB|^2) }}\) \(=(x-1)^2+(y-1)^2+(x-7)^2+(y-4)^2 \quad (*)\) \({\color{Red}{(问题转化为求式子(*)的取值范围,但是存在、两个变量,故想到消元) }}\) \(=2x^2+2y^2-16x-10y+67\) \(=10+16x+8y-16x-10y+67\)\({\color{Red}{(消元) }}\) \(=77-2y\), \(∵-3≤y≤7\),\({\color{Red}{(注意定义域的范围) }}\) \(∴63≤77-2y≤83\) 故\(|PA|^2+|PB|^2\)的取值范围是\([63 ,83]\). \({\color{Red}{方法2 }}\) 点\(P\)为\((x-4)^2+(y-2)^2=25\)上的一动点, 设\(P(4+5 \cos \alpha, 2+5 \sin \alpha)\), \({\color{Red}{(利用圆的参数方程,引入三角函数) }}\) 则\(|P A|^{2}+|P B|^{2}\) \(=(3+5 \cos \alpha)^{2}+(1+5 \sin \alpha)^{2}+(5 \cos \alpha-3)^{2}+(5 \sin \alpha-2)^{2}\) \(=73-10 \sin \alpha\) 所以\(63≤|PA|^2+|PB|^2≤83\), 即\(|PA|^2+|PB|^2\)的取值范围是\([63 ,83]\). 【点拨】本题注意是利用函数思想求解,把所求几何量用某个(或某些)变量表示,故设元引入变量很重要,本题是设\(P(x ,y)\)或\(P(4+5 \cos \alpha, 2+5 \sin \alpha)\),最后达到几何问题代数化. 【典题2】已知直线\(l:y=x\),圆\(C:x^2+y^2-4x+3=0\),在\(l\)上任意取一点\(A\),向圆\(C\)作切线,切点分别为\(M\),\(N\),则原点\(O\)到直线\(MN\)的距离\(d\)的最大值为\(\underline{\quad \quad}\).
【解析】
\({\color{Red}{(代数法思路:要求d的最大值,则把直线MN的方程求出,再用点到直线距离公式把d用某个或某些变量表示出来,那点M, N是怎么产生的呢?是由点A确定的,故设元A(a ,a)) }}\)
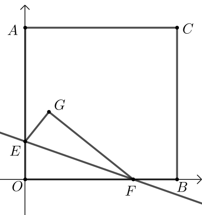
【典题3】已知实数\(x\)、\(y\)满足方程\(x^2+y^2-4x+1=0\). (1)求\(y-x\)的最大值和最小值; (2)求\(x^2+y^2\)的最大值和最小值; (3)求\(\dfrac{y}{x+1}\)的取值范围. 【解析】实数\(x\)、\(y\)满足方程\(x^2+y^2-4x+1=0\),化为\((x-2)^2+y^2=3\), 它表示一个圆,其参数方程为\(\left\{\begin{array}{c} x=2+\sqrt{3} \cos \alpha \\ y=\sqrt{3} \sin \alpha \end{array}\right.\); (1)\(y-x=\sqrt{3} \sin \alpha-(2+\sqrt{3} \cos \alpha)\)\(=\sqrt{3} \sin \alpha-\sqrt{3} \cos \alpha-2=\sqrt{6} \sin \left(\alpha-\dfrac{\pi}{4}\right)-2\) \(\because-1 \leq \sin \left(\alpha-\dfrac{\pi}{4}\right) \leq 1\), \(∴y-x\)的最小值为\(-2-\sqrt{6}\),最大值为\(-2+\sqrt{6}\); (2)\(x^{2}+y^{2}=(2+\sqrt{3} \cos \alpha)^{2}+(\sqrt{3} \sin \alpha)^{2}=4 \sqrt{3} \cos \alpha+7\), \(∴x^2+y^2\)的最大值为\(7+4 \sqrt{3}\),最小值为\(7-4 \sqrt{3}\); (3)\(\dfrac{y}{x+1}=\dfrac{\sqrt{3} \sin \alpha}{3+\sqrt{3} \cos \alpha}=\dfrac{\sin \alpha}{\sqrt{3}+\cos \alpha}\), 令\(t=\dfrac{\sin \alpha}{\sqrt{3}+\cos \alpha}\), \({\color{Red}{ (整体代换) }}\) \(\therefore t \cos \alpha-\sin \alpha=\sqrt{3} t \Rightarrow \sqrt{t^{2}+1} \sin (\alpha-\varphi)=\sqrt{3} t\), 则\(\sin (\alpha-\varphi)=\dfrac{\sqrt{3} t}{\sqrt{t^{2}+1}}\),由\(-1 \leq \dfrac{\sqrt{3} t}{\sqrt{t^{2}+1}} \leq 1\),解得\(-\dfrac{\sqrt{2}}{2} \leq t \leq \dfrac{\sqrt{2}}{2}\) 则\(\dfrac{y}{x+1}\)的最大值为\(\dfrac{\sqrt{2}}{2}\),最小值为\(-\dfrac{\sqrt{2}}{2}\). 【点拨】 ① 圆\((x-a)^2+(y-b)^2=r^2\)的参数方程\(\left\{\begin{array}{l} x=r \cos \theta+a \\ y=r \sin \theta+b \end{array}\right.\)(\(θ\)是参数); ② 本题方法是三角变换; ③ 这三个问题在前面也有所涉及,可以用几何方法求解,我们要比较下它们的优劣性. 【典题4】如图,在平面直角坐标系\(xOy\)中,正方形\(OABC\)的边长为\(4\),\(E(0 ,1)\),点\(F\)是正方形边\(OC\)上的一个动点,点\(O\)关于直线\(EF\)的对称点为\(G\)点,当\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\)取得最小值时,直线\(GF\)的方程为\(\underline{\quad \quad}\).
【解析】\({\color{Red}{方法一\quad 函数法 }}\)
\({\color{Red}{(利用对称性求点G坐标,进而求|\overrightarrow{G A}+3 \overrightarrow{G B}|的表达式,其运动“源头”是点F(t,0),则表达式是关于t的) }}\)
设\(F(t ,0)\),\((00)\).
则\(\dfrac{b}{a} \times\left(-\dfrac{1}{t}\right)=-1\),\(\dfrac{a}{2 t}+\dfrac{b}{2}=1\),
解得\(a=\dfrac{2 t}{1+t^{2}}\),\(b=\dfrac{2 t^{2}}{1+t^{2}}\),
\(\therefore G\left(\dfrac{2 t}{1+t^{2}}, \dfrac{2 t^{2}}{1+t^{2}}\right)\).
\(\because \overrightarrow{G A}+3 \overrightarrow{G B}=(-a, 4-b)+3(4-a, 4-b)=(12-4 a, 16-4 b)\).
\(\therefore|\overrightarrow{G A}+3 \overrightarrow{G B}|\)
\(=\sqrt{(12-4 a)^{2}+(16-4 b)^{2}}\)
\(=2 \sqrt{(3-a)^{2}+(4-b)^{2}}\)
\(=2 \sqrt{\left(3-\dfrac{2 t}{1+t^{2}}\right)^{2}+\left(4-\dfrac{2 t^{2}}{1+t^{2}}\right)^{2}}\)
\(=2 \sqrt{13-12 \cdot \dfrac{t-1}{1+t^{2}}}\),
令\(m=t-1∈(-1 ,3]\),则\(|\overrightarrow{G A}+3 \overrightarrow{G B}|=2 \sqrt{13-12 \cdot \dfrac{m}{m^{2}+2 m+2}}\)
易得\(f(m)=\dfrac{m}{m^{2}+2 m+2}=\left\{\begin{array}{cc}
0, & m=0 \\
\dfrac{1}{m+\dfrac{2}{m}+2} & , m \in(-1,0) \cup(0,3]
\end{array}\right.\)的最大值
在\(m=\sqrt{2}\),即\(t=\sqrt{2}+1\)时取到,
此时\(G\left(\dfrac{\sqrt{2}}{2}, 1+\dfrac{\sqrt{2}}{2}\right)\),\(F(\sqrt{2}+1,0)\),
易得直线\(GF\)方程为\(y=-x+1+\sqrt{2}\).
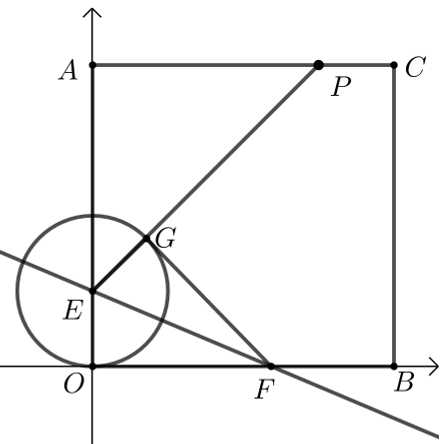
\({\color{Red} { 方法二\quad 几何法}}\)
设点\(G(a ,b)\),
\(∵\)点\(O\)关于直线\(EF\)的对称点为\(G\)点,\(∴EG=OE=1\),
\(∴\)点\(G\)的轨迹是以\(E\)为圆心,半径为\(1\)的圆\(\odot E:a^2+(b-1)^2 =1\),
\(\because \overrightarrow{G A}+3 \overrightarrow{G B}=(-a, 4-b)+3(4-a, 4-b)=(12-4 a, 16-4 b)\)
\(\therefore|\overrightarrow{G A}+3 \overrightarrow{G B}|=\sqrt{(12-4 a)^{2}+(16-4 b)^{2}}=2 \sqrt{(3-a)^{2}+(4-b)^{2}}\),
设点\(P(3 ,4)\), \({\color{Red}{(利用圆外一定点到圆上一点的距离最值模型) }}\)
则\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\)取到最小值时,即点\(P\)到圆\(\odot E\)上一点最短距离之时,
此时点\(G\)为直线\(EP:y=x+1\)与圆\(\odot E\)的交点,
由\(\left\{\begin{array}{c} y=x+1 \\ x^{2}+(y-1)^{2}=1 \end{array}\right.\)解得\(x=\dfrac{\sqrt{2}}{2}\),\(y=1+\dfrac{\sqrt{2}}{2}\), 即\(G\left(\dfrac{\sqrt{2}}{2}, 1+\dfrac{\sqrt{2}}{2}\right)\), 此时\(GF⊥EP\),故直线\(GF\)的斜率为\(-1\), 故直线\(GF\)方程为\(y=-x+1+\sqrt{2}\). \({\color{Red}{方法三\quad 三角代换 }}\) 如方法二,得到\(a^2+(b-1)^2 =1\),可设\(a=\sinα ,b=1+\cosα\), 则\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\) \(=\sqrt{(12-4 a)^{2}+(16-4 b)^{2}}\) \(=2 \sqrt{(3-\sin \alpha)^{2}+(3-\cos \alpha)^{2}}\) \(=2 \sqrt{19-6 \sqrt{2} \sin \left(\alpha+\dfrac{\pi}{4}\right)}\), 当\(\alpha=\dfrac{\pi}{4}\),即\(G\left(\dfrac{\sqrt{2}}{2}, 1+\dfrac{\sqrt{2}}{2}\right)\)时,\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\)取到最小值. 设点\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\), 由\(GF=OF\)得\(\sqrt{\left(t-\dfrac{\sqrt{2}}{2}\right)^{2}+\left(1+\dfrac{\sqrt{2}}{2}\right)^{2}}=t\),解得\(t=\sqrt{2}+1\), 易得直线\(GF\)方程为\(y=-x+1+\sqrt{2}\). 【点拨】 ① 题中\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\)看不出明显的几何意义,故用代数的方法处理这个条件; ② 细品三种方法,各有千秋, \((i)\)函数法思路朴素,易入手,要求出\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\),则设元\(G(a ,b)\),而点\(G\)是由点\(F\)确定的,转而设元\(F(t ,0)\),从而易得\(a\)、\(b\)用\(t\)表示,从而\(|\overrightarrow{G A}+3 \overrightarrow{G B}|\)用\(t\)表示,求出其最小值时\(t\)的取值问题较不难了,就计算量有些大; \((ii)\)几何法,重在发现图中几何变量内在关系,需要认真观察图象,有一定思考难度,若想到计算量上较函数法小不少;本题是确定了动点\(G\)的轨迹是圆,相当找到\(a\),\(b\)的关系,而\(|\overrightarrow{G A}+3 \overrightarrow{G B}|=2 \sqrt{(3-a)^{2}+(4-b)^{2}}\)联想到圆外一定点到圆上一点的距离最值模型. \((iii)\)方法三的三角代换只是在几何法的基础上作了一些计算的简化工作,体现到三角代换在某些情境中设元的优势. 巩固练习1(★★)若实数\(x\),\(y\)满足\(x^2+y^2+4x-2y-4=0\),则\(\sqrt{x^{2}+y^{2}}\)的最大值是( ) A.\(\sqrt{5}+3\) \(\qquad \qquad\)B.\(6 \sqrt{5}+14\) \(\qquad \qquad\) C.\(-\sqrt{5}+3\)\(\qquad \qquad\) D.\(-6 \sqrt{5}+14\) 2(★★★)[多选题]若实数\(x\),\(y\)满足条件\(x^2+y^2=1\),则下列判断正确的是( ) A.\(x+y\)的范围是\([0, \sqrt{2}]\) B.\(x^2-4x+y^2\)的范围是\([-3 ,5]\) C.\(xy\)的最大值为\(1\) D.\(\dfrac{y-2}{x+1}\)的范围是\(\left(-\infty,-\dfrac{3}{4}\right]\) 3(★★★)[多选题]已知点\(P(2 ,4)\),若过点\(Q(4 ,0)\)的直线\(l\)交圆\(C:(x-6)^{2}+y^{2}=9\)于\(A\),\(B\)两点,\(R\)是圆\(C\)上动点,则( ) A.\(|AB|\)的最小值为\(2 \sqrt{5}\) B.\(P\)到\(l\)的距离的最大值为\(2 \sqrt{5}\) C.\(\overrightarrow{P Q} \cdot \overrightarrow{P R}\)的最小值为\(12-2 \sqrt{5}\) D.\(|PR|\)的最大值为\(4 \sqrt{2}+3\) 4(★★)已知点\(A(1 ,1)\),\(B(2 ,2)\),点\(P\)在直线\(y=\dfrac{1}{2} x\)上,求\(|PA|^2+|PB|^2\)取得最小值时\(P\)点的坐标. 5(★★★)在平面直角坐标系\(xOy\)中,圆\(C\)的方程为\((x-2)^{2}+y^{2}=1\),\(M\)为圆\(C\)的圆心,过原点\(O\)的直线\(l\)与圆\(C\)相交于\(A\),\(B\)两点(\(A\),\(B\)两点均不在\(x\)轴上).求\(△ABM\)面积的最大值. 6(★★★)过点\(P(2,1)\)的直线\(l\)与\(x\)轴、\(y\)轴正半轴交于\(A\),\(B\)两点,求满足下列条件的直线\(l\)的方程,\(O\)为坐标原点, (1)\(△AOB\)面积最小时;(2)\(|OA|+|OB|\)最小时;(3)\(|PA|⋅|PB|\)最小时. 7(★★★)已知直线\(l\)过定点\(P(-2 ,1)\),且交\(x\)轴负半轴于点\(A\)、交\(y\)轴正半轴于点\(B\),点\(O\)为坐标原点. (1)若\(△AOB\)的面积为\(4\),求直线\(l\)的方程; (2)求\(|OA|+|OB|\)的最小值,并求此时直线\(l\)的方程; (3)求\(|PA|⋅|PB|\)的最小值,并求此时直线\(l\)的方程. 8(★★★)在平面直角坐标系\(xOy\)中.已知圆\(C\)经过\(A(0 ,2)\),\(O(0 ,0)\),\(D(t ,0)\)\((t>0)\)三点,\(M\)是线段\(AD\)上的动点,\(l_1\)\(,l_2\)是过点\(B(1 ,0)\)且互相垂直的两条直线,其中\(l_1\)交\(y\)轴于点\(E\),\(l_2\)交圆\(C\)于\(P\),\(Q\)两点. (1)若\(t=PQ=6\),求直线\(l_2\)的方程; (2)若\(t\)是使\(AM≤2BM\)恒成立的最小正整数,求\(△EPQ\)的面积的最小值. 参考答案1.\(A\) 2.\(BD\) 3.\(ABD\) 4.\(\left(\dfrac{9}{5}, \dfrac{9}{10}\right)\) 5.\(\dfrac{1}{2}\) 6.\((1) x+2y-4=0 \quad \text { (2) } x+\sqrt{2} y-2-\sqrt{2}=0 \quad (3) x+y-3=0\) 7.\((1) 4x-3y-1=0 \quad \text { (2) } \dfrac{\sqrt{15}}{2}\) |
【本文地址】




 \({\color{Red}{理解 }}\) 如图,易得\(r\cosθ=\)有向线段HM\(=x-a⇒x=r\cosθ+a\),
\(r\sinθ=\)有向线段\(HP=y-b⇒y=r\sinθ+b\).
\({\color{Red}{ Eg }}\)圆\((x+1)^2+(y-2)^2=9\)的参数方程为\(\left\{\begin{array}{l}
x=3 \cos \theta-1 \\
y=3 \sin \theta+2
\end{array}\right.\).
\({\color{Red}{理解 }}\) 如图,易得\(r\cosθ=\)有向线段HM\(=x-a⇒x=r\cosθ+a\),
\(r\sinθ=\)有向线段\(HP=y-b⇒y=r\sinθ+b\).
\({\color{Red}{ Eg }}\)圆\((x+1)^2+(y-2)^2=9\)的参数方程为\(\left\{\begin{array}{l}
x=3 \cos \theta-1 \\
y=3 \sin \theta+2
\end{array}\right.\).




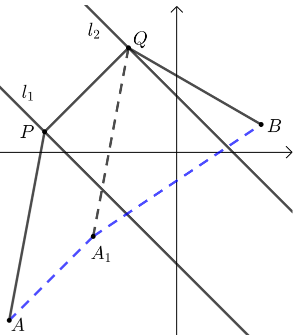 取点\(A_1 (m,n)\),使得\(k_{A A_{1}}=1\),\(A A_{1}=\dfrac{3 \sqrt{2}}{2}\),
则\(\dfrac{n+3}{m+3}=1 ,\sqrt{(m+3)^{2}+(n+3)^{2}}=\dfrac{3 \sqrt{2}}{2}\),
解得\(m=-\dfrac{3}{2}\),\(n=-\dfrac{3}{2}\),即\(A_{1}\left(-\dfrac{3}{2},-\dfrac{3}{2}\right)\),
此时四边形\(AA_1 QP\)是平行四边形,
则\(|A P|+|P Q|+|Q B|=\left|A A_{1}\right|+\left|A_{1} Q\right|+|Q B|=\dfrac{3 \sqrt{2}}{2}+\left|A_{1} Q\right|+|Q B|\),
显然\(\left(\left|A_{1} Q\right|+|Q B|\right)_{\min }=A_{1} B\),
所以\(|A P|+|P Q|+|Q B|\)的最小值\(\sqrt{13}+\dfrac{3 \sqrt{2}}{2}\).
【点拨】求形如\(\sqrt{(x-a)^{2}+(y-b)^{2}}+\sqrt{(x-c)^{2}+(y-d)^{2}}\)的式子最值,可理解为动点\((x ,y)\)与定点\((a ,b)\)、\((c ,d)\)的距离之和的最值问题;这充分把代数问题几何化,与斜率型的题型一样,我们要充分理解,比如求式子\(\dfrac{|3 x-4 y+1|}{5}\)的最值你又会想到我们学过的什么公式么?
取点\(A_1 (m,n)\),使得\(k_{A A_{1}}=1\),\(A A_{1}=\dfrac{3 \sqrt{2}}{2}\),
则\(\dfrac{n+3}{m+3}=1 ,\sqrt{(m+3)^{2}+(n+3)^{2}}=\dfrac{3 \sqrt{2}}{2}\),
解得\(m=-\dfrac{3}{2}\),\(n=-\dfrac{3}{2}\),即\(A_{1}\left(-\dfrac{3}{2},-\dfrac{3}{2}\right)\),
此时四边形\(AA_1 QP\)是平行四边形,
则\(|A P|+|P Q|+|Q B|=\left|A A_{1}\right|+\left|A_{1} Q\right|+|Q B|=\dfrac{3 \sqrt{2}}{2}+\left|A_{1} Q\right|+|Q B|\),
显然\(\left(\left|A_{1} Q\right|+|Q B|\right)_{\min }=A_{1} B\),
所以\(|A P|+|P Q|+|Q B|\)的最小值\(\sqrt{13}+\dfrac{3 \sqrt{2}}{2}\).
【点拨】求形如\(\sqrt{(x-a)^{2}+(y-b)^{2}}+\sqrt{(x-c)^{2}+(y-d)^{2}}\)的式子最值,可理解为动点\((x ,y)\)与定点\((a ,b)\)、\((c ,d)\)的距离之和的最值问题;这充分把代数问题几何化,与斜率型的题型一样,我们要充分理解,比如求式子\(\dfrac{|3 x-4 y+1|}{5}\)的最值你又会想到我们学过的什么公式么?



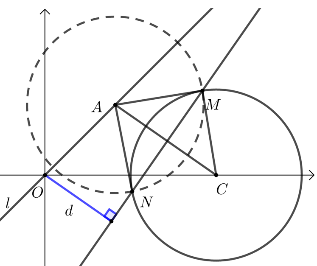 由题可得圆\(C\)的圆心坐标为\((2 ,0)\),半径为\(1\).
\(∵A\)在直线\(l\)上,设\(A(a ,a)\),
又\(M\)、\(N\)为过\(A\)点的圆的切线的切点,
故有\(AM^2=AN^2=AC^2-1\),
\(∴\)以\(A\)为圆心,\(AM\)为半径的圆方程为\((x-a)^{2}+(y-a)^{2}=(a-2)^{2}+a^{2}-1\),
化简得\(x^2+y^2-2ax-2ay-3+4a=0\),
\({\color{Red}{(把MN看成圆C与圆A的公共弦,可求出直线MN的直线方程) }}\)
\(∴MN\)所在直线方程为\((2-a)x-ay+2a-3=0\), \({\color{Red}{(圆A方程减去圆C方程便是) }}\)
\(∴O\)到\(MN\)的距离\(d=\dfrac{|2 a-3|}{\sqrt{(2-a)^{2}+a^{2}}}\), \({\color{Red}{ (问题最后变成求函数的最值)}}\)
\(\therefore d^{2}=2+\dfrac{1-4 a}{2 a^{2}-4 a+4}\),
令\(1-4a=t\),得\(d^{2}=2+\dfrac{8 t}{t^{2}+6 t+25}=2+\dfrac{8}{t+\dfrac{25}{t}+6}\),
由不等\(t+\dfrac{25}{t} \geq 10\),当且仅当\(t=5\),即\(a=-1\)时取等.
\(\therefore d \leq \dfrac{\sqrt{10}}{2}\),即原点\(O\)到直线\(MN\)的距离\(d\)的最大值为\(\dfrac{\sqrt{10}}{2}\).
【点拨】
① 代数法设元很重要,那我们首先要理解题意,明白几何问题中各量之间的“因果关系”方能找到“源头”;
② 过两圆\(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\),\(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为\(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\),此圆系不含\(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地,当\(λ=-1\)时,上述方程为一次方程;两圆相交时,表示公共弦方程;
③ 本题最后涉及到的函数是\(f(x)=\dfrac{a_{1} x^{2}+b_{1} x+c_{1}}{a_{2} x^{2}+b_{2} x+c_{2}}\))型,对其最值的求法要掌握好,它在高二也常考.
由题可得圆\(C\)的圆心坐标为\((2 ,0)\),半径为\(1\).
\(∵A\)在直线\(l\)上,设\(A(a ,a)\),
又\(M\)、\(N\)为过\(A\)点的圆的切线的切点,
故有\(AM^2=AN^2=AC^2-1\),
\(∴\)以\(A\)为圆心,\(AM\)为半径的圆方程为\((x-a)^{2}+(y-a)^{2}=(a-2)^{2}+a^{2}-1\),
化简得\(x^2+y^2-2ax-2ay-3+4a=0\),
\({\color{Red}{(把MN看成圆C与圆A的公共弦,可求出直线MN的直线方程) }}\)
\(∴MN\)所在直线方程为\((2-a)x-ay+2a-3=0\), \({\color{Red}{(圆A方程减去圆C方程便是) }}\)
\(∴O\)到\(MN\)的距离\(d=\dfrac{|2 a-3|}{\sqrt{(2-a)^{2}+a^{2}}}\), \({\color{Red}{ (问题最后变成求函数的最值)}}\)
\(\therefore d^{2}=2+\dfrac{1-4 a}{2 a^{2}-4 a+4}\),
令\(1-4a=t\),得\(d^{2}=2+\dfrac{8 t}{t^{2}+6 t+25}=2+\dfrac{8}{t+\dfrac{25}{t}+6}\),
由不等\(t+\dfrac{25}{t} \geq 10\),当且仅当\(t=5\),即\(a=-1\)时取等.
\(\therefore d \leq \dfrac{\sqrt{10}}{2}\),即原点\(O\)到直线\(MN\)的距离\(d\)的最大值为\(\dfrac{\sqrt{10}}{2}\).
【点拨】
① 代数法设元很重要,那我们首先要理解题意,明白几何问题中各量之间的“因果关系”方能找到“源头”;
② 过两圆\(C_1:x^2+y^2+D_1 x+E_1 y+F_1=0\),\(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为\(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\),此圆系不含\(C_2:x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地,当\(λ=-1\)时,上述方程为一次方程;两圆相交时,表示公共弦方程;
③ 本题最后涉及到的函数是\(f(x)=\dfrac{a_{1} x^{2}+b_{1} x+c_{1}}{a_{2} x^{2}+b_{2} x+c_{2}}\))型,对其最值的求法要掌握好,它在高二也常考.