| MATLAB线性规划学习笔记 | 您所在的位置：网站首页 › 线性规划问题实验心得体会 › MATLAB线性规划学习笔记 |
MATLAB线性规划学习笔记
|
目录
线性规划的标准型一般线性规划问题的数学表达式标准型：一般线性规划问题的matlab标准型：
线性规划例题例题1：线性回归问题的线性规划求解例题2：飞机轰炸
小结
线性规划的标准型
一般线性规划问题的数学表达式标准型：
a和b构成约束条件，用来约束决策变量。 一般线性规划问题的matlab标准型：
向量x 的值。还有其它的一些函数调用形式（在 Matlab 指令窗运行 help linprog 可以看到所有的函数调 用形式），如： OPTIONS 是控制参数。 线性规划例题 例题1：线性回归问题的线性规划求解
为了建立线性规划模型，我们引入绝对离差的概念 。用d 1 i _{1i} 1i表示正离差，d 2 i _{2i} 2i表示负离差 （离差值均大于0）。则我们可以得到如下线性规划约束等式： MATLAB代码求解如下： clear all x=[143,145,146,147,149,150,153,154,155,156,157,158,159,160,162,164]'; y=[88,85,88,91,92,93,93,95,96,98,97,96,98,99,100,102]'; n=ones(size(x)); Aeq=[n,x]; beq=y; A=[];b=[]; k=length(x); f=[0 0]; lb=[-100,-100];ub=[100,100]; for i=1:k%构造约束条件，和决策变量 p=zeros(k,2); f=[f,1,1]; lb=[lb,0,0]; ub=[ub,100,100]; p(i,:)=[1,-1]; Aeq=[Aeq,p]; end [d,fval]=linprog(f,A,b,Aeq,beq,lb,ub) h=140:0.1:164; g=d(1)+d(2).*h; X=[n,x]; b=regress(y,X);%调用线性回归的regress函数 g1=b(1)+b(2).*h; plot(x',y','*',h,g,'-',h,g1,'-','LineWidth',1); legend('实际投点','绝对值偏差','regress函数') grid onx和y的值是网上找的一个线性回归问题的数据。决策变量一共有34个，前两个为我们所需要的拟合直线 的系数，后面的变量均为正负离差值。就是b 0 _{0} 0,b 1 _{1} 1,d 11 _{11} 11,d 21 _{21} 21,d 12 _{12} 12,d 22 _{22} 22,… 这是Aeq的数据结构如下：
本文给出了线性规划的基本模型，和简单的求解方法。第一道例题侧重于约束函数的构造以及决策变量的构造技巧，第二道例题侧重于将非线性问题线性化。 参考文献：【1】线性规划在多元线性回归中的解法及应用。张爱兰，唐虹。昆明理工大学学报（自然科学版）39卷第1期，2014年2月。 |
其中z是目标函数，x是决策变量，c是决策权重。
一般求解线性规划问题采用 matlab中的linprog函数。基本函数形式为 linprog(c,A,b)，它的返回值是
这里fval 返回目标函数的值，LB 和UB 分别是变量x 的下界和上界，x
0
_{0}
0 是x 的初始值，
通常的回归问题会采用最小二乘法解决。但是最小二乘法的有时候并不理想
其中
ϵ
\epsilon
ϵ为拟合值与真实值的偏差的大小。
可以很容易推知，d
1
i
_{1i}
1i+d
2
i
_{2i}
2i就是第i组观测值y
i
_{i}
i与拟合值之间的绝对离差。因此可以用线性规划问题解决绝对离差和的最小估计问题。 
I
n
_{n}
n为n阶单位矩阵
这是f的数据结构： 
前两位归为0，是因为我们的目标函数中没有用到拟合直线的系数。 结果如下：
这个题目的约束条件比较明了，关键是构造目标函数。从题意得出，一共有8种选择，记每种选择的成功概率为a
i
_{i}
i,则根据概率论中独立事件的计算公式我们可以得到目标函数：
然而，线性规划只能接受线性的目标函数和约束条件，所以我们还要进一步将目标函数线性化。 
这样就将问题转化为可以用matlab标准型求解的问题了。 代码如下：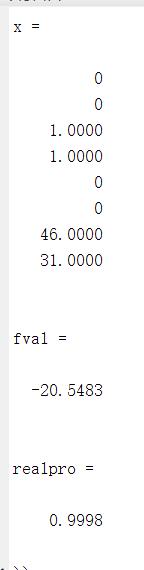
最后结果显示，最优方案可以使概率极为接近1.【本文地址】