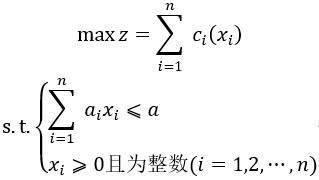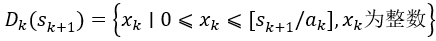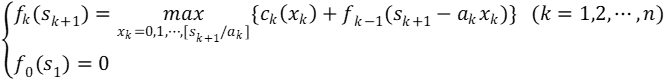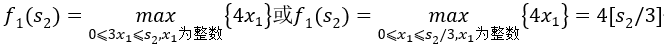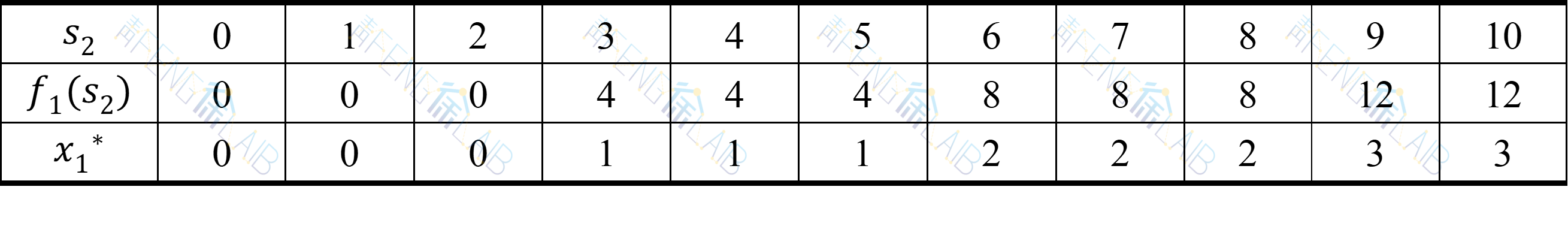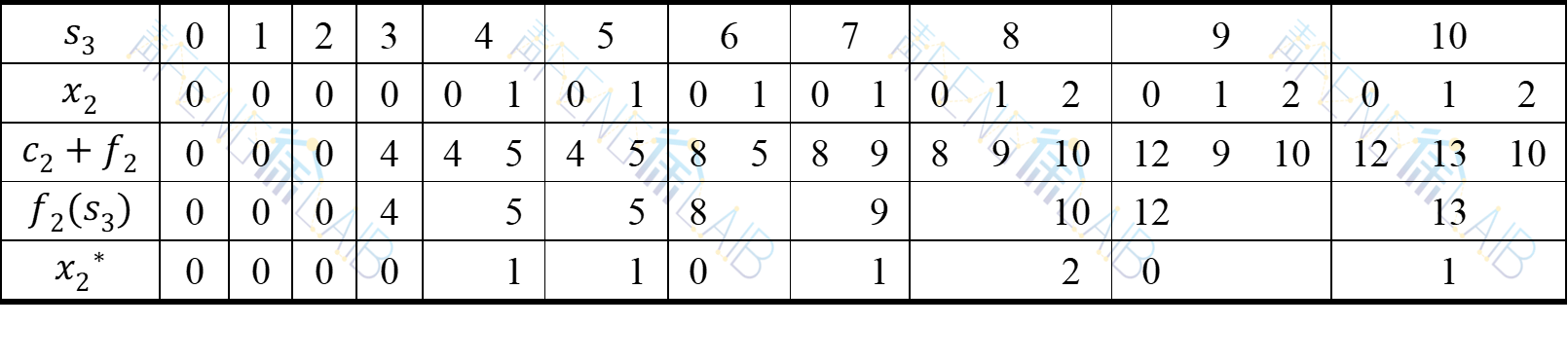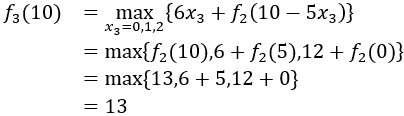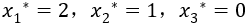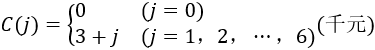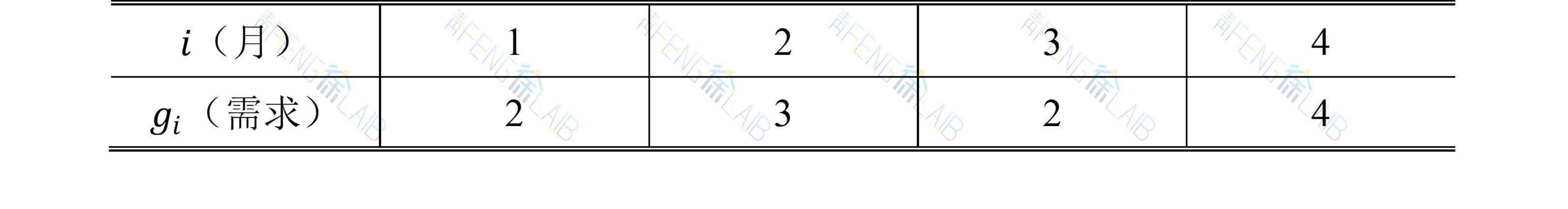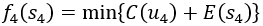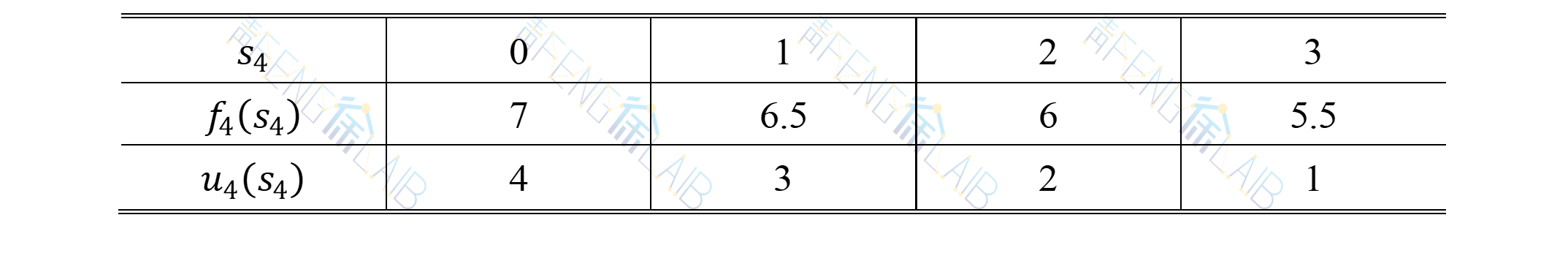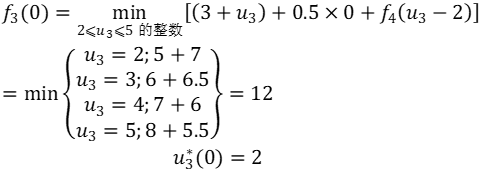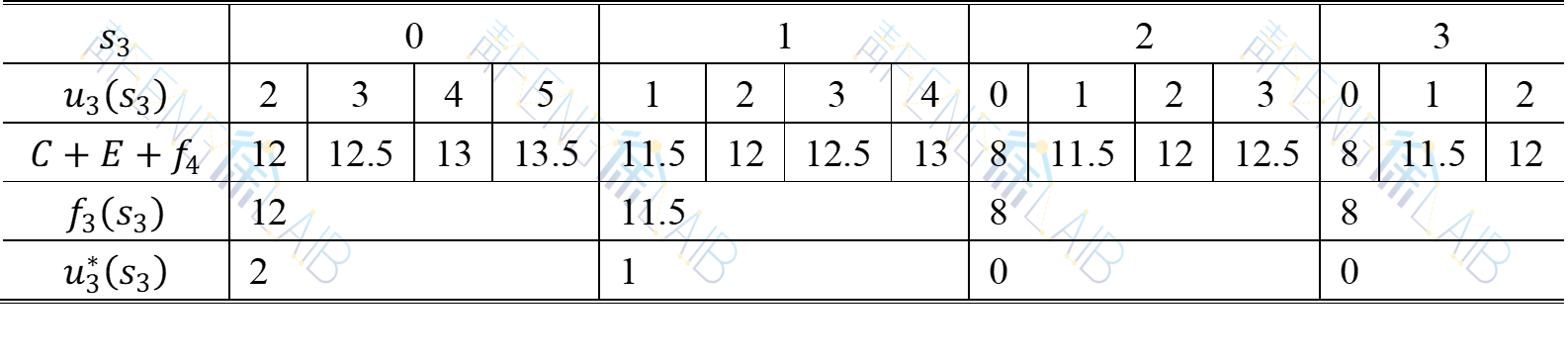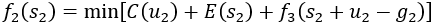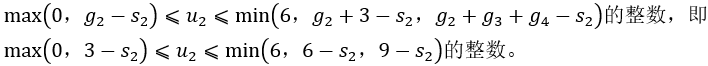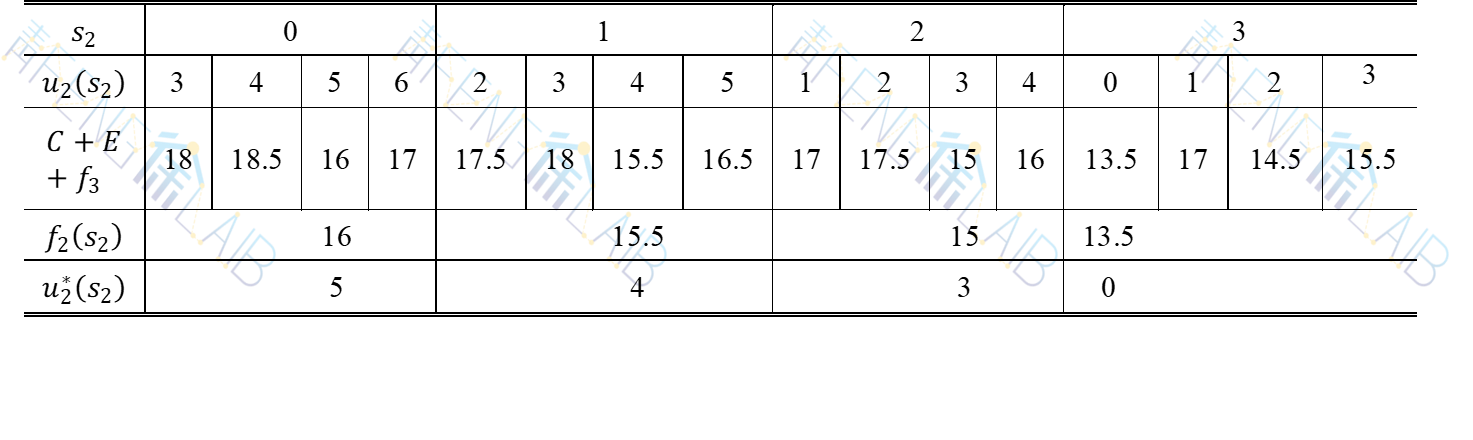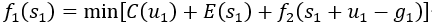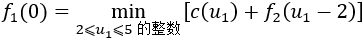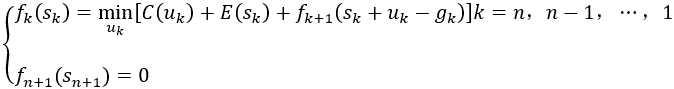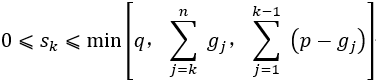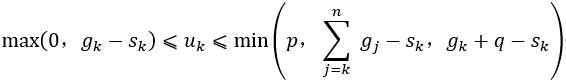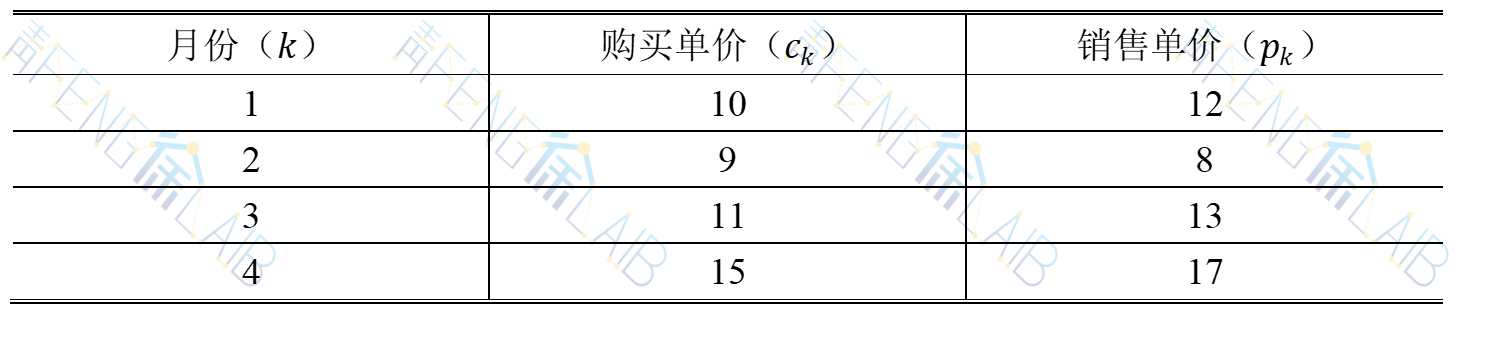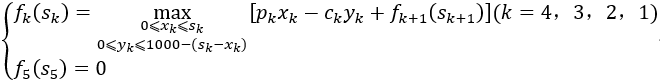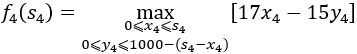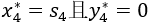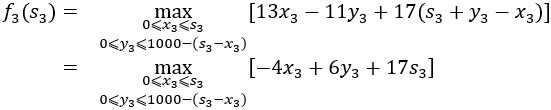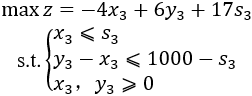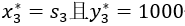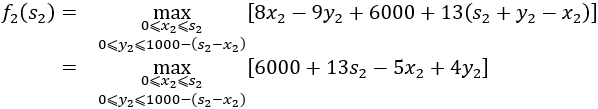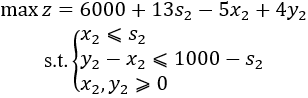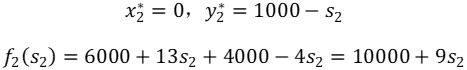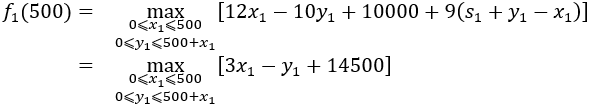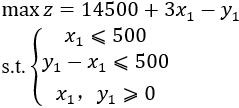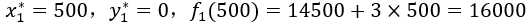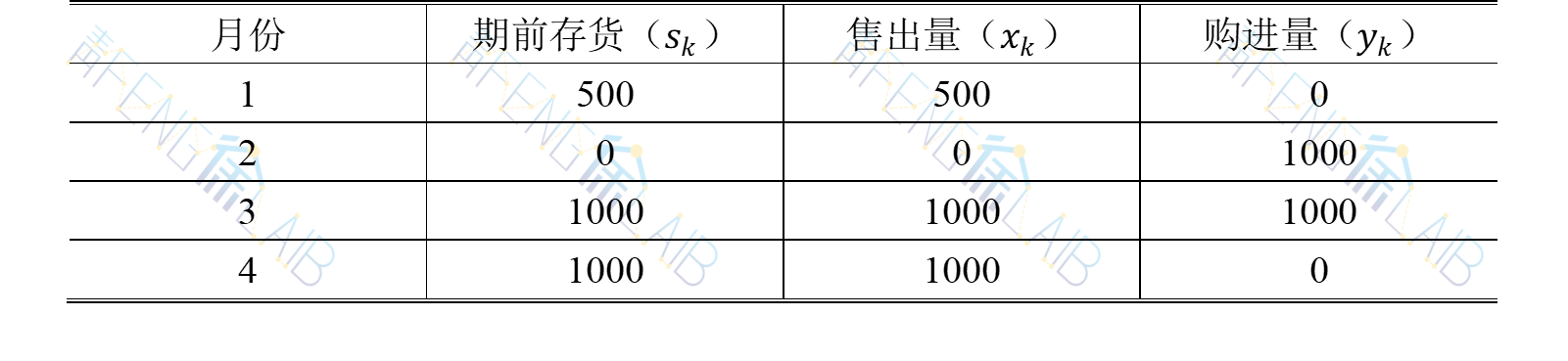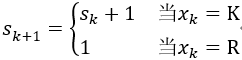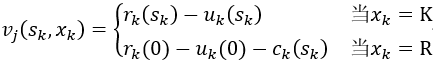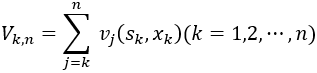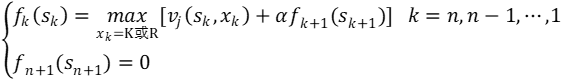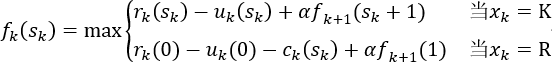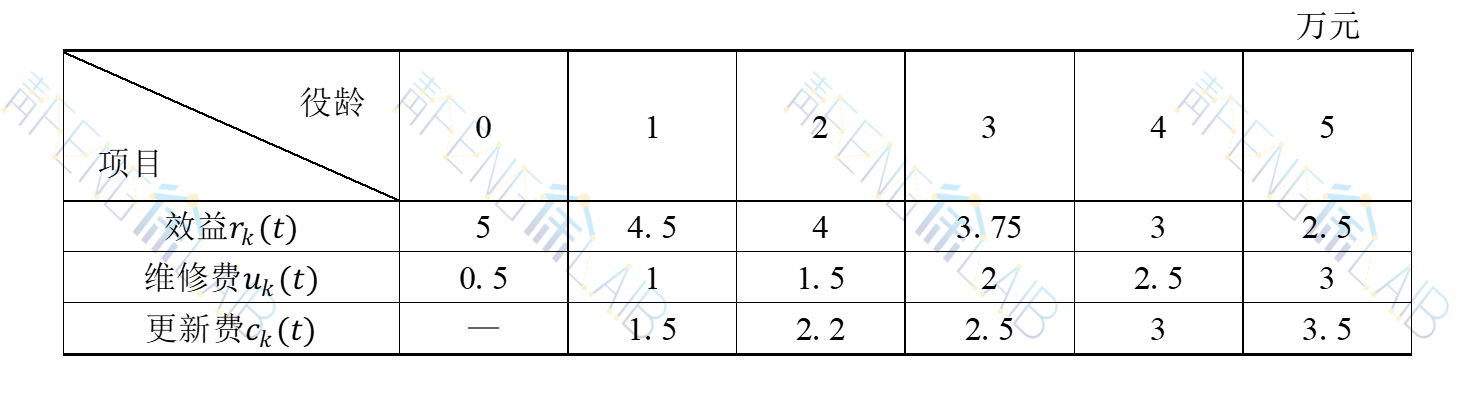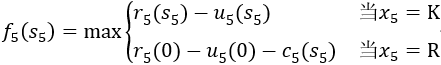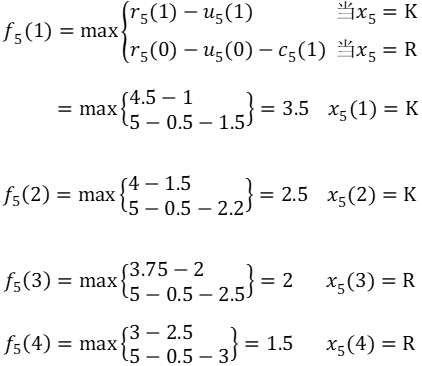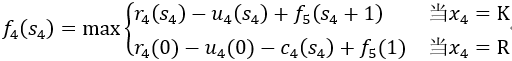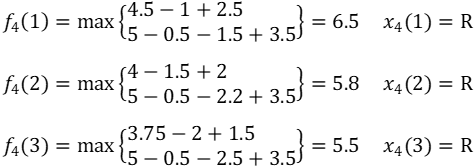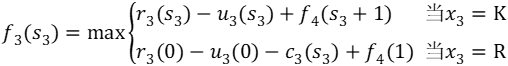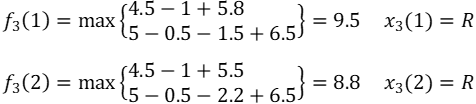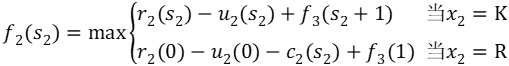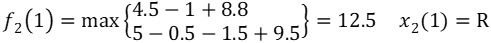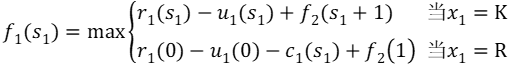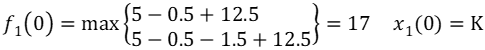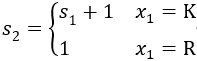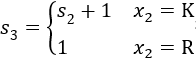运筹说第69期

2024-07-15 01:52| 来源: 网络整理| 查看: 265

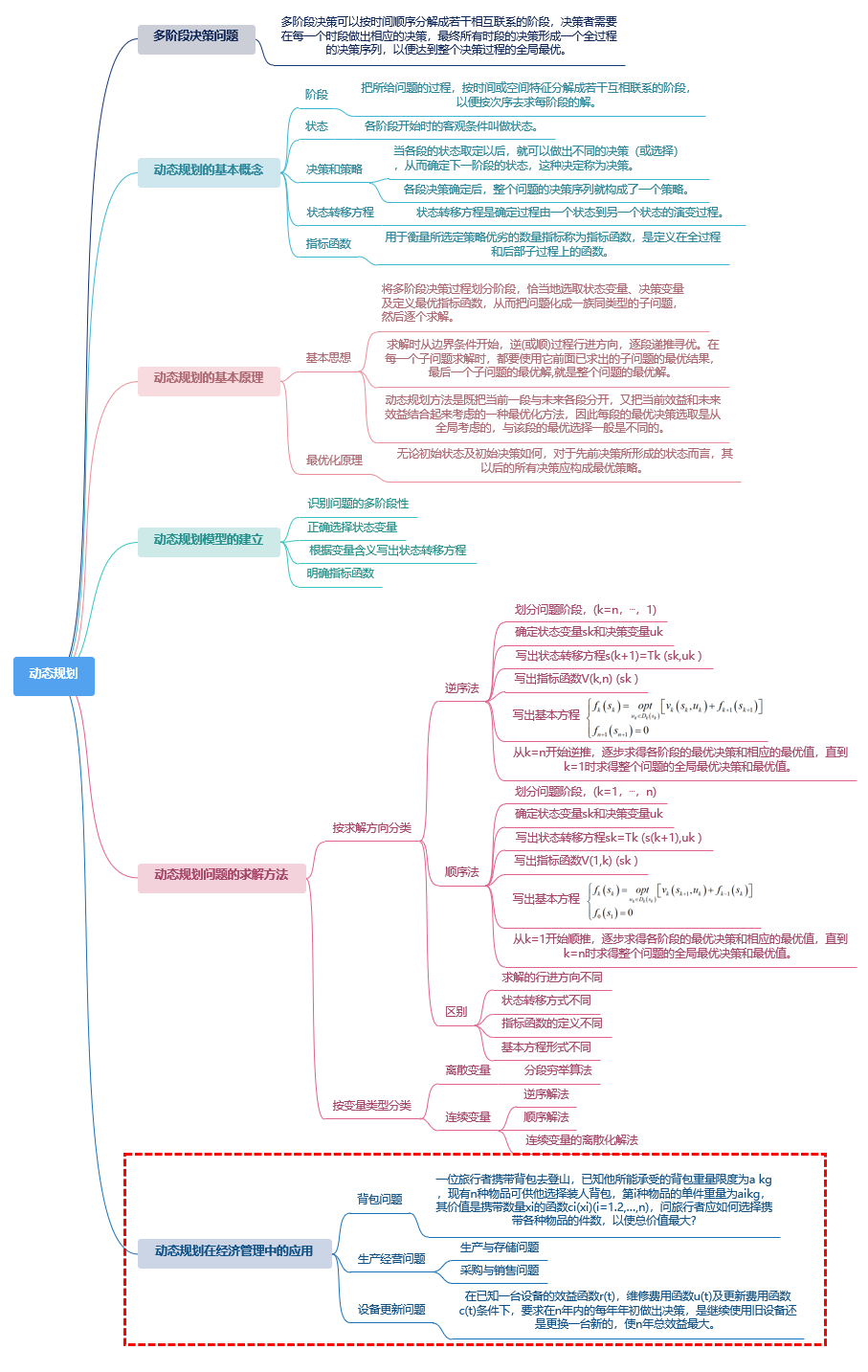
通过前几期的学习，我们已经学会了动态规划的基本概念和基本原理，并且掌握了动态规划模型的建立和具体的求解方法，本期小编带大家学习动态规划在经济管理中的应用。

除了前面讲到的最优路径、资源分配问题外，动态规划在经济管理中还有许多应用，小编选择了其中一些典型例子，包括背包问题、生产经营问题和设备更新问题，进行详细讲解。

1.背包问题

接下来我们先从经典的背包问题开始讲起。

背包问题又称装载问题，一般提法是：一位旅行者携带背包去登山，已知他所能承受的背包重量限度为akg，现有n种物品可供他选择装入背包，第i种物品的单件重量为aikg，其价值（可以是表明本物品对登山的重要性的数量指标）是携带数量xi的函数ci(xi)（i=1,2,…,n），问旅行者应如何选择携带各种物品的件数，以使总价值最大？

背包问题等同于车、船、人造卫星等工具的最优装载，有广泛的实用意义。

设xi为第i种物品装入的件数，则背包问题可归结为如下形式的整数规划模型：

下面用动态规划顺序解法来进行建模求解。

阶段k：将可装入物品按1，2，…，n排序，每段装一种物品，共划分为n个阶段，即k=1,2,…,n。

状态变量sk+1：在第k段开始时，背包中允许装入前k种物品的总重量。

决策变量xk：装入第k种物品的件数。

状态转移方程：sk=sk+1-akxk

允许决策集合：

其中[sk+1/ak]表示不超过sk+1/ak的最大整数。

最优指标函数fk(sk+1)表示在背包中允许装入物品的总重量不超过sk+1kg，采用最优策略只装前k种物品时的最大使用价值。

则可得到动态规划的顺序递推方程为

用顺序解法逐步计算出f1(s2)，f2(s3)，…，fk(sk+1)及相应的决策函数x1(s2)，x2(s3)，…，xn(sn+1)，最后得到的fn(a)即为所求的最大价值，相应的最优策略则由反推计算得出。

例1 背包问题

有一辆最大货运量为10t的卡车，用以装载3种货物，每种货物的单位重量及相应单位价值如下表所示。应如何装载可使总价值最大？

解：设第i种货物装载的件数为xi（i=1,2,3），则问题可表示为：

可按前述方式建立动态规划模型，由于决策变量取离散值，所以可以用列表法求解。

当k=1时，

计算结果如下表所示。

当k=2时，

计算结果见下表。

当k=3时，

此时有x3*=0，逆推可得全部策略为：

最大价值为13。

2.生产经营问题

生产经营问题又可以分为两类：生产与储存问题、采购与销售问题，下面我们通过两道例题来学习一下。

例2 生产与储存问题

某工厂生产并销售某种产品，已知今后四个月市场需求预测如下表所示，又每月生产j单位产品费用为

每月库存j单位产品的费用为E(j)=0.5j(千元)，该厂最大库存容量为3单位，每月最大生产能力为6单位，计划开始和计划期末库存量都是零。试制订四个月的生产计划，在满足用户需求条件下总费用最小。假设第i+1个月的库存量是第i个月可销售量与该月用户需求量之差；而第i个月的可销售量是本月初库存量与产量之和。

用动态规划法求解时，对有关概念做如下分析：

（1）阶段：每个月为一个阶段，k=1，2，3，4。

（2）状态变量：sk为第k个月初的库存量。

（3）决策变量：uk为第k个月的生产量。

（4）状态转移方程：sk+1=sk+uk-gk

（5）最优指标函数：fk(sk)表示第k月状态为sk时，采取最佳策略生产，从本月到计划结束（第4月末）的生产与存储最低费用。

考虑k=4，因为要求四月底库存为零，本月需求为4，所以本月产量应为u4=4-s4，由于库存量最大为3，所以s4取值只能是0，1，2，3。

可以列出f4(s4)和u4(s4)，见表1。

当k=3时，先分析状态变量s3的取值范围，它与库存能力、生产能力、需求量均有关，在此由最大库存量决定s3={0，1，2，3}。再分析决策变量u3的允许决策集合，为满足本月需求，产量u3至少为g3-s3=2-s3，若库存量s3>2，则u3应取0。为保证期末库存量为零，u3不能超过g3+g4-s3=6-s3，另外u3还受最大库存量3的限制，即不能超过g3+3-s3=5-s3，同时还受最大生产能力6的限制，总之有

我们对s3=0，1，2，3分别求出f3(s3)的值，当s3=0时，

这就是说，若第三个月初库存为零，则三、四两个月最低费用为12(千元)，第三个月最优产量为2个单位。依此类推，可得表2。

当k=2时，有

其中状态变量s2={0，1，2，3}。

决策变量u2为

本段计算结果如表3所示。

当k=1时，有

由于状态s1=0，本月产量u1同样要受本月需求量、最大库存容量、最大生产能力等约束限制，应为2⩽u1⩽5的整数，则

计算结果见表4。

由上表可知，总最低费用为f1(0)=21(千元)，第一个月最佳产量为2单位。而需求g1=2，所以第二个月初库存量为零，再由表3中查s2=0列可得第二个月最佳产量为5单位，同理通过查表2、表1可得第三、第四月的最佳产量。

即最佳生产计划为：第一个月生产2单位，第二个月生产5单位，第三个月不生产，第四个月生产4单位。

总结上述解题过程，可得此类生产存储问题的基本方程为

若最大库存量为q，每月最大生产能力为p，则状态集合为

允许决策集合为

例3 采购与销售问题

某商店在未来的4个月里，准备利用它的一个仓库来专门经销某种商品，仓库最大容量能储存这种商品1000单位。假定该商店每月只能卖仓库现有的货。当商店在某月购货时，下月初才能到货。预测该商品未来四个月的买卖价格如下表所示，假定商店在1月开始经销时，仓库储有该商品500单位。试问若不计库存费用，该商店应如何制订1月至4月的订购与销售计划，使预期获利最大。

解：按月份划分为4个阶段，k=1，2，3，4

状态变量sk：第k月初时仓库中的存货量(含上月订货)。

决策变量xk：第k月卖出的货物数量。

决策变量yk：第k月订购的货物数量。

状态转移方程：sk+1=sk+yk-xk

最优指标函数fk(sk)：第k月初存货量为sk时，从第k月到4月末所获最大利润。则有逆序递推关系式为

当k=4时

显然，决策应取

才有最大值f4(s4)=17s4

当k=3时

这个阶段需求解一个线性规划问题：

当满足

有最大值f3(s3)=6000+13s3

当k=2时

则求解线性规划问题：

得到

当k=1时

解线性规划问题：

得决策

最优策略如下表所示。最大利润为16000。

3.设备更新问题

企业中经常会遇到一台设备应该使用多少年更新最合算的问题。一般来说，一台设备在比较新时，年运转量大，经济收入高，故障少，维修费用少，但随着使用年限的增加，年运转量减少因而收人减少，故障变多维修费用增加。如果更新可提高年净收入，但是当年要支出一笔数额较大的购买费。设备更新问题的一般提法：在已知一台设备的效益函数r(t)，维修费用函数u(t)及更新费用函数c(t)条件下，要求在n年内的每年年初做出决策，是继续使用旧设备还是更换一台新的，使n年总效益最大。

设rk(t)：在第k年设备已使用过t年（或称役龄为t年），再使用1年时的效益。

uk(t)：在第k年设备役龄为t年，再使用一年的维修费用。

ck(t)：在第k年卖掉一台役龄为t年的设备，买进一台新设备的更新净费用。

α为折扣因子（0≤α≤1），表示一年以后的单位收入价值相当于现年的α单位。

下面建立动态规划模型。

阶段k（k=1，2，…，n）表示计划使用该设备的年限数。

状态变量sk：第k年年初，设备已使用过的年数，即役龄。

决策变量xk：是第k年年初更新，还是保留使用旧设备，分别用R与K表示。

状态转移方程为