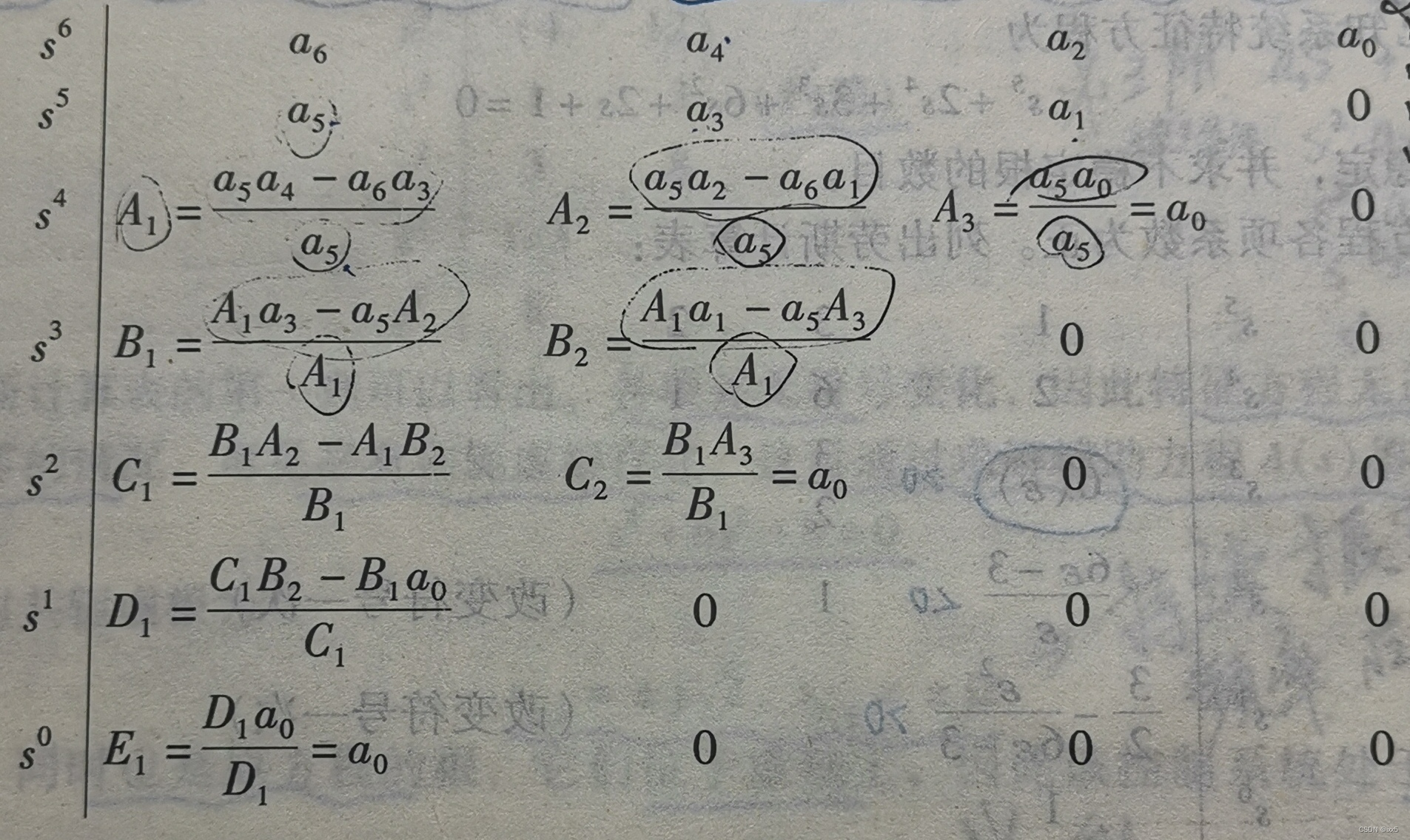| 02 | 您所在的位置:网站首页 › 系统特征方程怎么求 › 02 |
02
|
线性系统稳定性及劳斯判据
稳定性线性系统稳定性判别准则系统稳定的充要条件
劳斯判据不同类型情况的计算方法劳斯稳定性判据的充要条件劳斯计算表(1)特征方程不缺项(2)第一列数值存在0值(3)存在全0行
稳定性
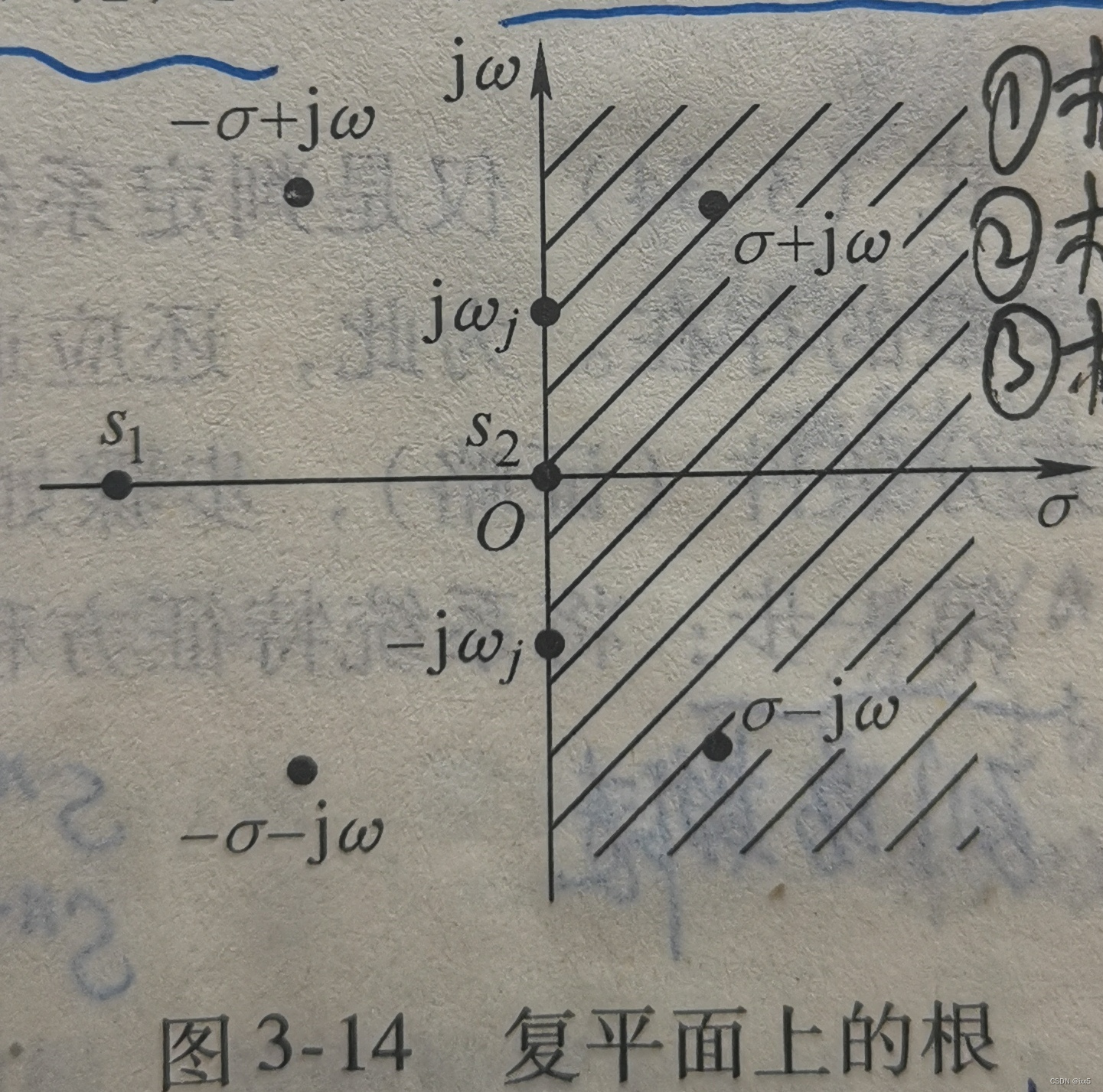
稳定性,是指控制系统在任意足够小的偏差作用下,其过度过程随着时间的推移是否具有逐渐恢复原平衡状态的性能。 当系统受到扰动后,系统最终恢复原平衡状态,即系统输出c(t)逐渐收敛,为系统稳定;当系统受到扰动后,扰动消除,系统的输出c(t)会出现逐渐发散振荡或者等幅振荡,为系统不稳定。 线性系统稳定性判别准则根据稳定性的定义,系统稳定性与系统的输入无关,是系统的固有特性。由此来推出线性系统稳定性的判别准则。 设线性系统的微分方程: a n d n c ( t ) d t n + a n − 1 d n − 1 c ( t ) d t n − 1 + . . . + a 1 d c ( t ) d t + a 0 c ( t ) = b m d m r ( t ) d t m + b m − 1 d m − 1 r ( t ) d t m − 1 + . . . + b 1 d r ( t ) d t + b 0 r ( t ) \ a_n \frac{d^n c(t)}{dt^n} + a_{n-1} \frac{d^{n-1} c(t)}{dt^{n-1}} +...+a_1 \frac{d c(t)}{dt} +a_0 c(t) \\ = \ b_m \frac{d^m r(t)}{dt^m} + b_{m-1} \frac{d^{m-1} r(t)}{dt^{m-1}} +...+b_1 \frac{d r(t)}{dt} +b_0 r(t) andtndnc(t)+an−1dtn−1dn−1c(t)+...+a1dtdc(t)+a0c(t)= bmdtmdmr(t)+bm−1dtm−1dm−1r(t)+...+b1dtdr(t)+b0r(t) c(t)–系统输入; r(t)–系统输出; (注:c、r可理解为输"入"、输"出"的汉语拼音首字母) 由于稳定性是研究去掉扰动后系统的运动情况,所以,令 a n d n c ( t ) d t n + a n − 1 d n − 1 c ( t ) d t n − 1 + . . . + a 1 d c ( t ) d t + a 0 c ( t ) = 0 \ a_n \frac{d^n c(t)}{dt^n} + a_{n-1} \frac{d^{n-1} c(t)}{dt^{n-1}} +...+a_1 \frac{d c(t)}{dt} +a_0 c(t) = 0 andtndnc(t)+an−1dtn−1dn−1c(t)+...+a1dtdc(t)+a0c(t)=0 得到齐次微分方程。 进行拉氏变换可得(初始状态为零): a n s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 = 0 \ a_n s^n + a_{n-1} s^{n-1} +...+ a_1 s + a_0 =0 ansn+an−1sn−1+...+a1s+a0=0 微分方程的解的一般式为: c ( t ) = k 1 e s 1 t + k 2 e s 2 t + . . . + k n e s n t \ c(t) = k_1 e^{s_1 t} + k_2 e^{s_2 t} +...+ k_n e^{s_n t} \\ c(t)=k1es1t+k2es2t+...+knesnt k_1 、k_2、…、k_n --由初始条件决定的积分常数; s_1、s_2、…、s_n–特征方程的根 这些特征值的根可以是实根也可以是复根,这里设q个实根,2r个复根,满足q + 2r = n ∏ i = 1 q a n ( s − s i ) ∏ j = 1 r [ s − ( σ j + j ω j ) ] [ s − ( σ j − j ω j ) ] = 0 \prod_{i=1}^q a_n (s - s_i) \prod_{j=1}^r [s - (\sigma_j +j\omega_j)] [s - (\sigma_j - j\omega_j)] = 0 i=1∏qan(s−si)j=1∏r[s−(σj+jωj)][s−(σj−jωj)]=0 改写成, y ( t ) = ∑ i = 1 q k i e s i t + ∑ j = 1 r e σ j t ( A j c o s ( ω j t ) + B j s i n ( ω j t ) ) y(t) = \sum_{i=1}^q k_i e^{s_i t} + \sum_{j=1}^r e^{\sigma_j t}(A_j cos(\omega_j t) + B_j sin(\omega_j t)) y(t)=i=1∑qkiesit+j=1∑reσjt(Ajcos(ωjt)+Bjsin(ωjt)) 系统稳定的充要条件由上式可得出, ① 如果s_i、σ_j都是负值,那么当t→∞时,c(t)→0, 这说明系统的特征方程的根是负实根或共轭复根具有复实部时,系统在稳态(t→∞)下必然是稳定的。 ② 反之,s_i、σ_j都是正值,那么当t→∞时,c(t)→∞,则c(t)是发散的,系统不稳定。 ③ 如果特征根的共轭复根的实部σ_j为0,c(t)中包含(A_j cos(ω_j t) + B_j sin(ω_j t)这样的振荡分量,便会出现临界振荡或称为系统临界稳定状态,工程上认为临界振荡也是一种不稳定; ④ 特征根为0,即落在原点处,则c(t)输出中包含常数项,相当于系统偏离平衡状态,所以系统不稳定。 综上,系统稳定性的判别可以归结为系统特征根的判别。系统稳定的充要条件:系统传递函数的特征根全部在[s]平面的左半平面。 如果传函为系统的闭环传函,形如 设控制系统的传递函数G(s) G ( s ) = b m s m + b m − 1 s m − 1 + . . . + b 1 s + b 0 a n s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 ( n ≥ m ) \ G(s)=\frac{b_m s^m +b_{m-1} s^{m-1} +...+b_1 s +b_0 }{a_n s^n +a_{n-1} s^{n-1} +...+a_1 s +a_0} (n \geq m) G(s)=ansn+an−1sn−1+...+a1s+a0bmsm+bm−1sm−1+...+b1s+b0(n≥m) 控制系统的特征方程为分母等于0的方程。 不同类型情况的计算方法有前面可知,传函的特征方程为 a n s n + a n − 1 s n − 1 + . . . + a 1 s + a 0 = 0 \ a_n s^n + a_{n-1} s^{n-1} +...+ a_1 s + a_0 =0 ansn+an−1sn−1+...+a1s+a0=0 这个多项式可以分解成一次因式(s +a)和二次因式(s^2 + bs +c)相乘的形式一次因式给出的是实根,二次因式可得出实根或者共轭复根。 当a、b、c都为正数时,特征方程的根才为负实数或复实部的共轭复数(二次方程的求根公式:x_1_2 =[-b±(b^ 2-4ac)^(1/2)]/2a)。 于是可知,特征多项式的系数a_n必须是正数,才能保证系统稳定(多项式的系数全为负可乘-1,变为正数)。 劳斯稳定性判据的充要条件①系统特征方程多项式的各项系数均大于零,即a_i > 0; ②劳斯计算表的第一列系数的符号相同(不变号,一般为大于零); 满足以上两个条件则说明系统稳定。 如果系统的s^n存在缺少项,则系统不稳定(结构不稳定) 劳斯计算表以六阶系统为例,展示劳斯计算表的计算方式:
a
6
s
6
+
a
5
s
5
+
a
4
s
4
+
a
3
s
3
+
a
2
s
2
+
a
1
s
+
a
0
=
0
\ a_6 s^6 + a_5 s^5 +a_4 s^4 +a_3 s^3 +a_2 s^2 + a_1 s + a_0 =0
a6s6+a5s5+a4s4+a3s3+a2s2+a1s+a0=0 系统的s^n存在缺少项,则系统不稳定(结构不稳定) (2)第一列数值存在0值这时可以使用无穷小值 ε 代替0做分母进行计算,在令ε→0时,判断第一列该项数值的符号 例: s 5 + 2 s 4 + 3 s 3 + 6 s 2 + 2 s + 1 = 0 判断系统是否稳定,并求出不稳定根的个数 \ s^5 +2 s^4 +3 s^3 +6s^2 + 2s + 1 =0 \\判断系统是否稳定,并求出不稳定根的个数 s5+2s4+3s3+6s2+2s+1=0判断系统是否稳定,并求出不稳定根的个数 s^5 1 3 2 s^4 2 6 1 s^3 0(ε) 3/2 s^2 (6ε - 3)/ε 1 (第一列符号改变一次) s^1 3/2 - ε^2/(6ε - 3) (第一列符号改变一次) s^0 1 --------------------- 当ε→0时,(6ε - 3)/ε → -∞ ,3/2 - ε^2/(6ε - 3) → 3/2,故特征值有两个正根。 (3)存在全0行在劳斯计算表中出现某一行各项全为0,这意味着在[s]平面存在一些对称(大小相等,符号相反)的根,包括实根和共轭复根。此时劳斯计算表由于全0行不能进行计算,这时,可将劳斯计算表全0行的上一行的数值作为系数构成"辅助方程",在对"辅助方程"进行求导,将求导后的系数替代全0行,继续计算。 例: s 6 + 2 s 5 + 8 s 4 + 12 s 3 + 20 s 2 + 16 s + 16 = 0 判断系统稳定性 \ s^6 + 2s^5 + 8s^4 + 12s^3 + 20s^2 + 16s + 16 =0 判断系统稳定性 s6+2s5+8s4+12s3+20s2+16s+16=0判断系统稳定性 s^6 1 8 20 16 s^5 (2 12 16) s^5 1 6 8 (化简) s^4 (2 12 16) s^4 1 6 8 (化简) s^3 0 0 ------------------ s^3行为全0行,使用s^3行的上一行s^4行的数值构造辅助方程 A(s) = s^4 + 6s^2 + 8 求导得,A'(s) = 4s^3 + 12s, 于是劳斯计算表改写成 ------------------ s^6 1 8 20 16 s^5 (2 12 16) s^5 1 6 8 (化简) s^4 (2 12 16) s^4 1 6 8 (化简) s^3 (4 12) s^3 1 3 (化简) s^2 3 8 s^1 1/3 s^0 8从劳斯计算表可以看出,第一列无符号变换,特征方程系数均大于0 ,但s^3行为全0行说明有共轭复根存在,可通过辅助方程A(s)求出,令 A(s)=0得 s^ 4 + 6s^2 + 8 = 0 解得两对共轭复根, s 1 , 2 = ± j 2 , s 3 , 4 = ± j 2 s_{1,2} = \pm j\sqrt {2} , s_{3,4} = \pm j 2 s1,2=±j2 ,s3,4=±j2 这两个共轭复根同时还是原特征方程的根,在[s]平面虚轴上,因此该控制系统处于临界振荡状态,为工程的不稳定状态。 另一类问题,类似极点配置例,D(s) = s^ 3 + 5k s^2 + (2k+3)s +10 (1) 求系统稳定时,k的取值范围; (2) k取何值时,系统处于振荡状态,并求出角频率;(类似上面求共轭复根) (3) 使s在[s]平面 Re= -1以左时,求k的范围;(提示:用s = s’ -1代替s,再对s’进行劳斯判据计算) |
【本文地址】
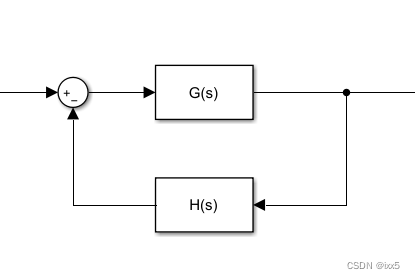 闭环传递函数:
G
t
(
s
)
=
G
(
s
)
1
+
G
(
s
)
H
(
s
)
\ G_t(s) = \frac{G(s)}{1+G(s)H(s)}
Gt(s)=1+G(s)H(s)G(s)
闭环传递函数:
G
t
(
s
)
=
G
(
s
)
1
+
G
(
s
)
H
(
s
)
\ G_t(s) = \frac{G(s)}{1+G(s)H(s)}
Gt(s)=1+G(s)H(s)G(s)