| 空间向量及其运算 | 您所在的位置:网站首页 › 空间两点向量平行公式 › 空间向量及其运算 |
空间向量及其运算
|
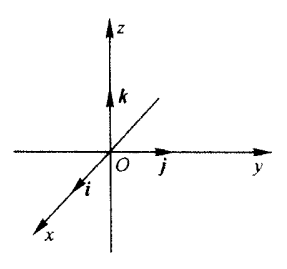
平面内任意向量 p \boldsymbol{p} p都可以用两个不共线的向量 a \boldsymbol{a} a b \boldsymbol{b} b来表示,这是平面向量的基本定理。类似的我们定义,如果三个向量不共面,那么对空间中的任一向量 p \boldsymbol{p} p,存在有序实数组 { x , y , z } \{x,y,z\} {x,y,z}使得 p = x a + y b + z c \boldsymbol{p}=x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c} p=xa+yb+zc,我们把向量 { a , b , c } \{\boldsymbol{a},\boldsymbol{b} ,\boldsymbol{c}\} {a,b,c}叫做空间的一个基底(base), a , b , c \boldsymbol{a},\boldsymbol{b} ,\boldsymbol{c} a,b,c叫做基向量(base vector),如果基向量两两垂直,则称这组基向量为正交向量;如果三个基向量两两垂直且为单位向量,则为单位正交向量。 一、空间直角坐标系以起点同为
O
O
O三个单位正交向量
i
,
j
,
k
\boldsymbol{i},\boldsymbol{j} ,\boldsymbol{k}
i,j,k所确定的三个轴依次叫做
x
x
x轴(横轴),
y
y
y轴(纵轴)和
z
z
z轴(竖轴),我们把
O
x
y
z
Oxyz
Oxyz或
[
O
;
i
,
j
,
k
]
[\boldsymbol{O};\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}]
[O;i,j,k]四者的组合称为直角坐标系。 设 a = ( a x , a y , a z ) \boldsymbol{a}=(a_x,a_y,a_z) a=(ax,ay,az), b = ( b x , b y , b z ) \boldsymbol{b}=(b_x,b_y,b_z) b=(bx,by,bz),其对应坐标表示 a = a x i + a y j + a z k b = b x i + b y j + b z k \boldsymbol{a}=a_x\boldsymbol{i}+a_y\boldsymbol{j}+a_z\boldsymbol{k}\quad \boldsymbol{b}=b_x\boldsymbol{i}+b_y\boldsymbol{j}+b_z\boldsymbol{k} a=axi+ayj+azkb=bxi+byj+bzk 2.1 向量线性运算基底形式: a + b = ( a x ± b x ) i + ( a y ± b y ) j + ( a z ± b z ) k \boldsymbol{a}+\boldsymbol{b}=(a_x\pm b_x)\boldsymbol{i}+(a_y \pm b_y)\boldsymbol{j}+(a_z\pm b_z)\boldsymbol{k} a+b=(ax±bx)i+(ay±by)j+(az±bz)k λ a = λ a x i + λ a y j + λ a z k \lambda \boldsymbol{a}=\lambda a_x\boldsymbol{i}+\lambda a_y\boldsymbol{j}+\lambda a_z\boldsymbol{k} λa=λaxi+λayj+λazk 坐标形式: a + b = ( a x ± b x , a y ± b y , a z ± b z ) \boldsymbol{a}+\boldsymbol{b}=(a_x \pm b_x,a_y \pm b_y,a_z\pm b_z) a+b=(ax±bx,ay±by,az±bz) λ a = ( λ a x , λ a y , λ a z ) \lambda \boldsymbol{a}=(\lambda a_x,\lambda a_y,\lambda a_z) λa=(λax,λay,λaz) 2.2 向量间的数量积运算数量积又称点积。设一物体在恒力
F
F
F作用下沿直线从点
M
1
M_1
M1移动到
M
2
M_2
M2以
s
s
s表示位移
M
1
M
2
→
\overrightarrow {M_1M_2}
M1M2
,物理学上告诉我们,力
F
F
F作的功为:
W
=
∣
F
∣
∣
s
∣
c
o
s
θ
W=|F||s|cos\theta
W=∣F∣∣s∣cosθ 其中
θ
\theta
θ是
F
F
F与
s
s
s的夹角。 由定义可知: a ⋅ a = ∣ a ∣ 2 \boldsymbol a \cdot \boldsymbol a=|a|^2 a⋅a=∣a∣2向量 a ⊥ b \boldsymbol a \bot\boldsymbol b a⊥b的充分必要条件是 a ⋅ b = 0 \boldsymbol a\cdot \boldsymbol b=0 a⋅b=0满足以下性质: 交换律 a ⋅ b \boldsymbol a \cdot \boldsymbol b a⋅b= b ⋅ a \boldsymbol b \cdot \boldsymbol a b⋅a结合律 ( a + b ) ⋅ c = a ⋅ c + b ⋅ c (\boldsymbol a + \boldsymbol b)\cdot\boldsymbol c=\boldsymbol a \cdot \boldsymbol c+\boldsymbol b \cdot \boldsymbol c (a+b)⋅c=a⋅c+b⋅cPS:向量夹角范围是 [ 0 , π ] [0,\pi] [0,π],所以不存在 a ⋅ b \boldsymbol a \cdot \boldsymbol b a⋅b和 b ⋅ a \boldsymbol b \cdot \boldsymbol a b⋅a夹角不一样的情况,都是一样的 θ \theta θ。优角是大于180度的角,劣角是小于或等于180度的角,因此向量夹角范围是劣角,在谈论向量夹角的时候,应该找小于或等于180度的角。 坐标形式的数量积 a ⋅ b = ( a x b x + a y b y + a z b z ) (1) \boldsymbol{a}\cdot\boldsymbol{b}=(a_xb_x+a_yb_y+a_zb_z)\tag{1} a⋅b=(axbx+ayby+azbz)(1) 2.3 向量积和混合积 向量积 a × b = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x ) (2) \boldsymbol{a}\times\boldsymbol{b}=(a_yb_z-a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x)\tag{2} a×b=(aybz−azby,azbx−axbz,axby−aybx)(2)混合积 略。 2.4 向量属性设向量坐标为: r = ( x , y , z ) \boldsymbol{r}=(x,y,z) r=(x,y,z),对应向量形式为: r = x i + y j + z k \boldsymbol{r}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k} r=xi+yj+zk, 模(大小) ∣ r ∣ = x 2 + y 2 + z 2 |\boldsymbol{r}|=x^2+y^2+z^2 ∣r∣=x2+y2+z2 设空间中的两点 A A A, B B B,其坐标分别为设 a = ( x 1 , y 1 , z 1 ) \boldsymbol{a}=(x_1,y_1,z_1) a=(x1,y1,z1), b = ( x 1 , y 2 , z 3 ) \boldsymbol{b}=(x_1,y_2,z_3) b=(x1,y2,z3) 根据三角或平行四边形法则, A B → = O B → − O A → = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) \overrightarrow {AB}=\overrightarrow {OB}-\overrightarrow {OA}=(x_2-x_1,y_2-y_1,z_2-z_1) AB =OB −OA =(x2−x1,y2−y1,z2−z1),其大小为 ∣ A B ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 |AB|=(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 ∣AB∣=(x2−x1)2+(y2−y1)2+(z2−z1)2 方向角和方向余弦 一个非零向量与三个坐标轴的夹角称为向量在坐标系下的方向角,对应的余弦值为方向余弦。三个方向余弦的平方和等于1。换句话说,一个向量在坐标系上有唯一的比例关系:余弦 - 投影(非常重要) 任何一个在数轴 u u u上的向量都可以在用一个数 λ \lambda λ和同方向的单位向量 e e e表示,如下: O M ′ → = λ e \overrightarrow{OM'}=\lambda{\boldsymbol{e}} OM′ =λe 这个数在数学上被称为向量 r \boldsymbol r r在 u \boldsymbol u u上的向量投影,记作 P r j u r Prj_u\boldsymbol{r} Prjur或 ( r ) u (\boldsymbol{r})_u (r)u。 按照投影的观点,直角坐标系上的一个向量 a \boldsymbol a a在直角坐标系 O x y z Oxyz Oxyz上的坐标为( a x , b x , c x a_x,b_x,c_x ax,bx,cx)就是向量 a \boldsymbol a a在三个坐标轴上的投影,也就是: a x = P r j x a , a y = P r j y a , a z = P r j z a a_x=Prj_x\boldsymbol a,a_y=Prj_y\boldsymbol a,a_z=Prj_z\boldsymbol a ax=Prjxa,ay=Prjya,az=Prjza 或者你更习惯这种表示方式: a x = ( a ) x , a y = ( a ) y , a z = ( a ) z a_x=(\boldsymbol a)_x,a_y=(\boldsymbol a)_y,a_z=(\boldsymbol a)_z ax=(a)x,ay=(a)y,az=(a)z 投影有以下性质: 性质1 ( a ) u = ∣ a ∣ c o s φ (\boldsymbol a)_u=|a|cos\varphi (a)u=∣a∣cosφ,其中 φ \varphi φ是向量 a \boldsymbol a a与 u \boldsymbol u u轴的夹角;性质2 ( a + b ) u = ( a ) u + ( b ) u (\boldsymbol a+\boldsymbol b)_u=(\boldsymbol a)_u+(\boldsymbol b)_u (a+b)u=(a)u+(b)u;性质3 ( λ a ) u = λ ( a ) u (\lambda \boldsymbol a)_u=\lambda (a)_u (λa)u=λ(a)u |
【本文地址】
 由
x
x
x和
y
y
y轴确定的平面叫做
x
O
y
xOy
xOy面,同理还有
x
O
z
xOz
xOz和
y
O
z
yOz
yOz,三个平面将空间划分为八个部分。如下图:
由
x
x
x和
y
y
y轴确定的平面叫做
x
O
y
xOy
xOy面,同理还有
x
O
z
xOz
xOz和
y
O
z
yOz
yOz,三个平面将空间划分为八个部分。如下图: 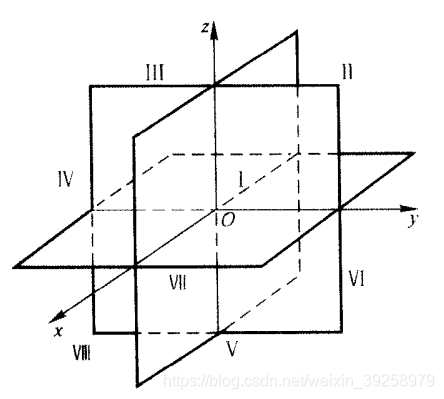 空间中任意一个向量都可以用坐标分解式表示。
空间中任意一个向量都可以用坐标分解式表示。 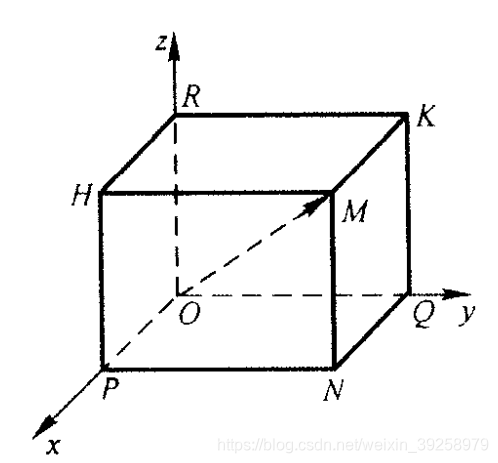 向量
r
=
O
M
→
=
O
P
→
+
P
N
→
+
N
M
→
=
O
P
→
+
O
Q
→
+
O
R
→
=
x
i
+
y
j
+
z
k
\boldsymbol{r}=\overrightarrow {OM}=\overrightarrow {OP}+\overrightarrow {PN}+\overrightarrow {NM}=\overrightarrow {OP}+\overrightarrow {OQ}+\overrightarrow {OR}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k}
r=OM
=OP
+PN
+NM
=OP
+OQ
+OR
=xi+yj+zk,这就建立了有序实数组(坐标)
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)、空间中向量
r
\boldsymbol{r}
r和空间中的点
M
M
M的联系。这些事实使得向量之间的运算与代数建立起了联系(即用数学计算来解决向量之间的关系)。
向量
r
=
O
M
→
=
O
P
→
+
P
N
→
+
N
M
→
=
O
P
→
+
O
Q
→
+
O
R
→
=
x
i
+
y
j
+
z
k
\boldsymbol{r}=\overrightarrow {OM}=\overrightarrow {OP}+\overrightarrow {PN}+\overrightarrow {NM}=\overrightarrow {OP}+\overrightarrow {OQ}+\overrightarrow {OR}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k}
r=OM
=OP
+PN
+NM
=OP
+OQ
+OR
=xi+yj+zk,这就建立了有序实数组(坐标)
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)、空间中向量
r
\boldsymbol{r}
r和空间中的点
M
M
M的联系。这些事实使得向量之间的运算与代数建立起了联系(即用数学计算来解决向量之间的关系)。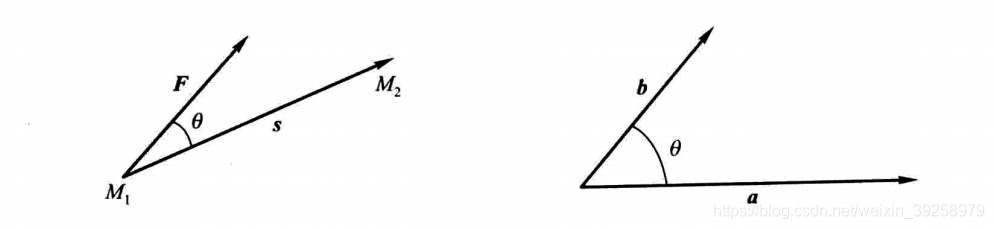 抽象成数学表达:
a
⋅
b
=
∣
a
∣
∣
b
∣
c
o
s
θ
\boldsymbol a \cdot \boldsymbol b=|a||b|cos\theta
a⋅b=∣a∣∣b∣cosθ
抽象成数学表达:
a
⋅
b
=
∣
a
∣
∣
b
∣
c
o
s
θ
\boldsymbol a \cdot \boldsymbol b=|a||b|cos\theta
a⋅b=∣a∣∣b∣cosθ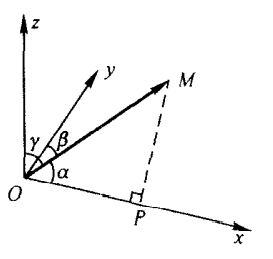
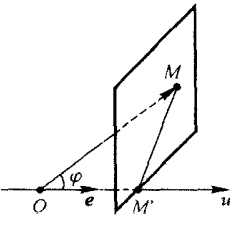 给定一个点
O
O
O和一个单位向量
e
\boldsymbol{e}
e可以确定一个延伸至无穷远的数轴
u
\boldsymbol u
u,在这个空间上任取一个向量记为
O
M
→
=
r
\overrightarrow{OM}=\boldsymbol{r}
OM
=r(平移至共起点),过待投影的向量
r
\boldsymbol r
r终点作一个垂直于数轴
u
u
u的平面,相交于
M
′
M'
M′(M在数轴
u
u
u的点投影),向量
O
M
′
→
\overrightarrow{OM'}
OM′
叫做向量
r
\boldsymbol{r}
r在
u
\boldsymbol u
u轴上的分向量。
给定一个点
O
O
O和一个单位向量
e
\boldsymbol{e}
e可以确定一个延伸至无穷远的数轴
u
\boldsymbol u
u,在这个空间上任取一个向量记为
O
M
→
=
r
\overrightarrow{OM}=\boldsymbol{r}
OM
=r(平移至共起点),过待投影的向量
r
\boldsymbol r
r终点作一个垂直于数轴
u
u
u的平面,相交于
M
′
M'
M′(M在数轴
u
u
u的点投影),向量
O
M
′
→
\overrightarrow{OM'}
OM′
叫做向量
r
\boldsymbol{r}
r在
u
\boldsymbol u
u轴上的分向量。