离散数学

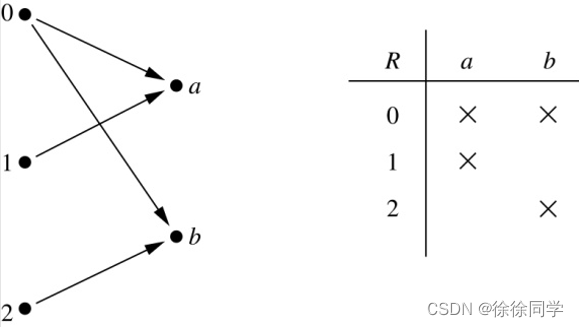
设A和B是集合，一个从 A 到 B 的二元关系是A×B的子集。 （序偶集合的子集）

🐳换句话说，一个从A到B的二元关系是集合R，其中每个有序对的第一个元素取自A而第二个元素取自B。

我们使用记号 aRb表示(a, b)∈R，aR b表示(a, b)∉R。当(a, b)属于R时，称a与b有关系R。

📘例：设 A = { 0, 1, 2 }， B = { a, b }

{ (0, a), (0, b), (1, a), (2, b) }是一个从 A 到 B 的关系。 我们可以用图或表格来表示从集合 A 到集合 B 的关系：

集合A上的关系是从A到A的关系。

🐳换句话说，集合A上的关系是从A到A的关系

📘例：设 A = { a, b, c } 那么R = { (a, a), (a, b), (a, c) }是 A 上的关系

A上的关系和 A × A 的子集是一回事 ➡所以可以直接计数 A × A 的子集。

因为当 A 是 n 元素集合时 A × A 有 n2 个元素，所以 A × A 的子集有 2m (m = n2)

📘例：设 B = { b } 那么B上的二元关系共有2个：R1 = ∅，R2 = { (b, b) }

📘例：设 C = { a, b, c } 那么C上的二元关系共有29 = 512个

若对每个元素a∈A有（a，a)∈R，那么定义在集合A上的关系R称为自反的 记作aRa，a是A中任意一个元素

用符号表示：（集合A上的关系）R 是自反的，当且仅当 ∀x（x∈A⟶ (x, x)∈R ）

（这里的论域是A中所有元素的集合。）

📘例： 以下关于整数的关系是自反的： R1 = { (a, b) | a ≤ b }， R3 = { (a, b) | a = b 或 a = – b }， R4 = { (a, b) | a = b }。

以下关系不是自反的： R2 = { (a, b) | a > b }（注意3 ≯ 3）， R5 = { (a, b) | a = b + 1 }（注意3 ≠ 3 + 1）， R6 = { (a, b) | a + b ≤ 3 }（注意4 + 4 ≰ 3）。

对于任意 a, b∈A，若只要 (a, b)∈R 就有 (b, a)∈R，则称定义在集合 A 上的关系 R 为对称的。

用符号表示：R 是对称的，当且仅当 ∀x∀y （ (x, y)∈R ⟶ (y, x)∈R ）

📘例： 以下关于整数的关系是对称的： R3 = { (a, b) | a = b 或 a = – b }， R4 = { (a, b) | a = b }， R6 = { (a, b) | a + b ≤ 3 }。

以下不是对称的： R1 = { (a, b) | a ≤ b }（反例：3 ≤ 4，但4 ≰ 3）， R2 = { (a, b) | a > b }（反例：4 > 3，但 3 ≯ 4）， R5 = { (a, b) | a = b + 1 }（反例：4 = 3 + 1，但3 ≠ 4 + 1）。

对于任意 a, b∈A，若 (a, b)∈R 且 (b, a)∈R，一定有 a = b，则称定义在集合 A 上的关系 R 为反对称的。

用符号表示：R 是反对称的，当且仅当 ∀x∀y（ (x, y)∈R ∧ (y, x)∈R ⟶ x = y ）

📘例： 以下关于整数的关系是反对称的： R1 = { (a, b) | a ≤ b }， R2 = { (a, b) | a > b }， R4 = { (a, b) | a = b }， R5 = { (a, b) | a = b + 1 }。

以下关系不是反对称的： R3 = { (a, b) | a = b 或 a = – b }（反例： (1, – 1) 和 (–1, 1) 都属于R3）， R6 = { (a, b) | a + b ≤ 3 }（反例： (1, 2) 和 (2, 1) 都属于R6）。

💻对称与反对称的概念不是对立的，因为一个关系可以同时有这两种性质或者两种性质都没有。 一个关系如果包含了某些形如(a，b）的有序对，其中a≠b，则这个关系就不可能同时是对称的和反对称的。

若对于任意 a, b, c∈A，(a, b)∈R 并且 (b, c)∈R 则 (a, c)∈R，那么定义在集合 A 上的关系 R 称为传递的。

用符号表示：R 是传递的，当且仅当∀x∀y∀z（ (x, y)∈R ∧ (y, z)∈R ⟶ (x, z)∈R）

📘例： 以下关于整数的关系是可传递的： R1 = { (a, b) | a ≤ b }， R2 = { (a, b) | a > b }， R3 = { (a, b) | a = b 或 a = – b }， R4 = { (a, b) | a = b }。

下面的句子不是可传递的： R5 = { (a, b) | a = b + 1 } （反例：(3, 2) 和 (4, 3) 都属于R5，但不属于 (3, 3)）， R6 = { (a, b) | a + b ≤ 3 } （反例：(2, 1) 和 (1, 2) 都属于R6，但不属于 (2, 2)）。

因为从A到B的关系是 A×B 的子集，所以可以按照两个集合组合的任何方式来组合两个从A到B的关系。

给定两个关系R1和R2，我们可以使用基本的集合操作将它们组合起来，形成新的关系，如 R1 ∪ R2、R1 ∩ R2、R1 − R2 和 R2 − R1

除了常见的并∪、交∩、差 - 、异或⊕，还有一种新的组合方式：

设R1 是集合 A 到集合 B 的关系，R2 是集合 B 到集合 C 的关系。 R2 和 R1 的合成是 A 到 C 的关系，其中如果 (x, y) 是 R1 的成员，(y, z) 是 R2的成员，那么 (x, z) 则是 R1 ∘ R2 的成员。

（R1 ∘ R2 表示R1 和 R2 的合成）

由两个关系合成的定义可以递归定义关系R的幂

设R为A上的二元关系，则关系R的n次幂Rn可归纳定义为： 基础步骤：R1 = R 归纳步骤：Rn+1 = Rn ∘ R

传递关系的幂是该关系的子集