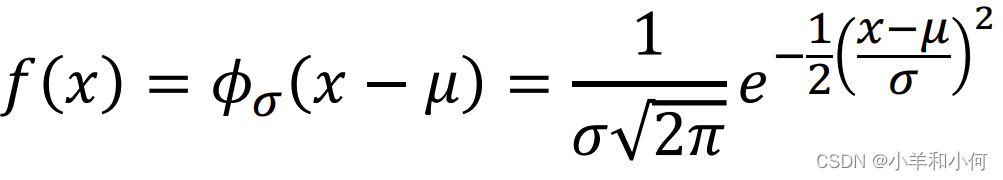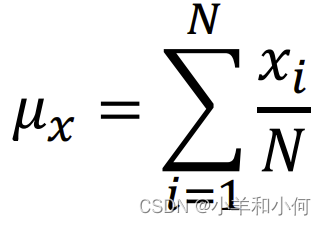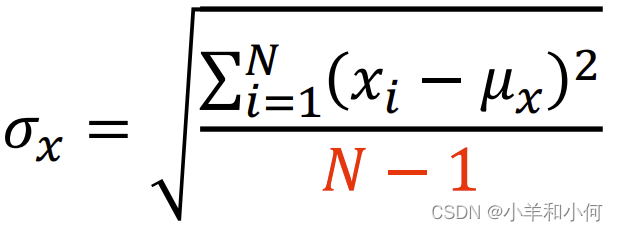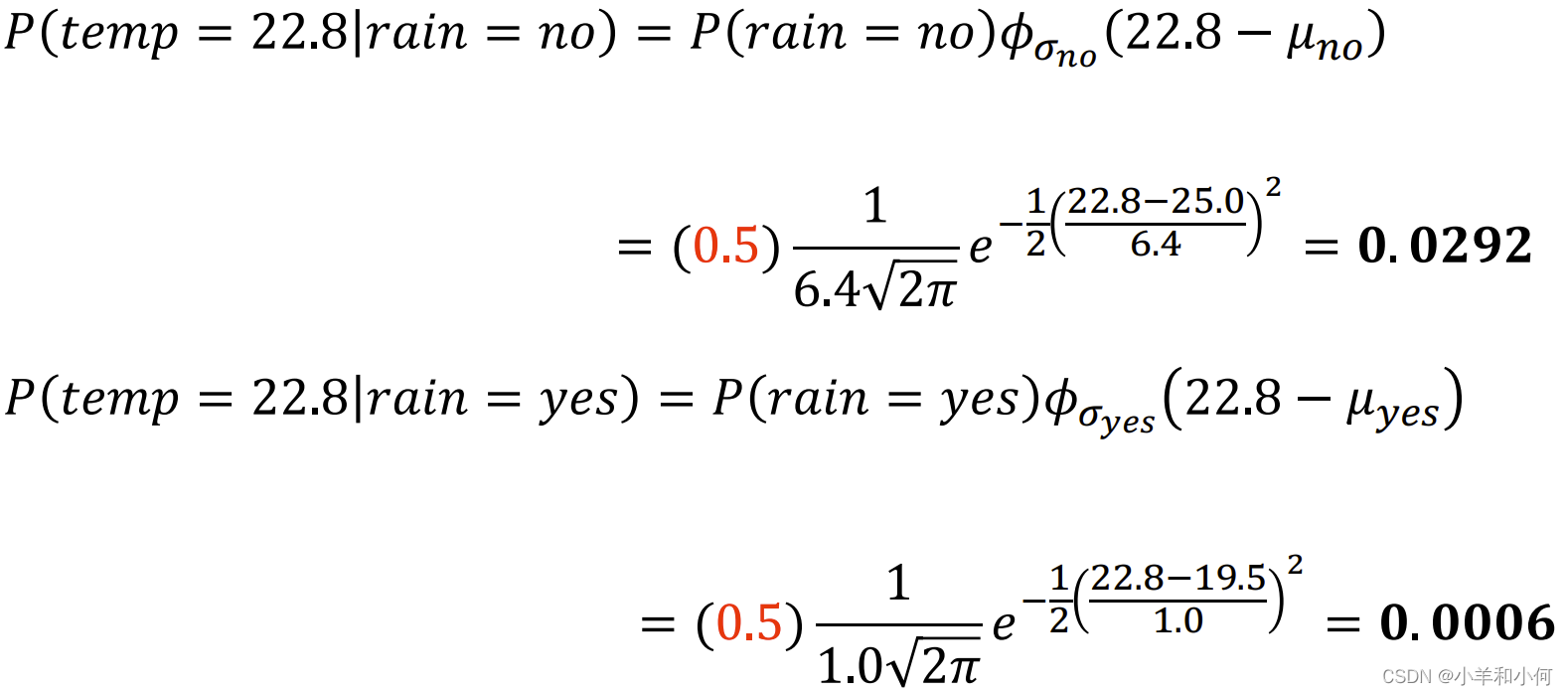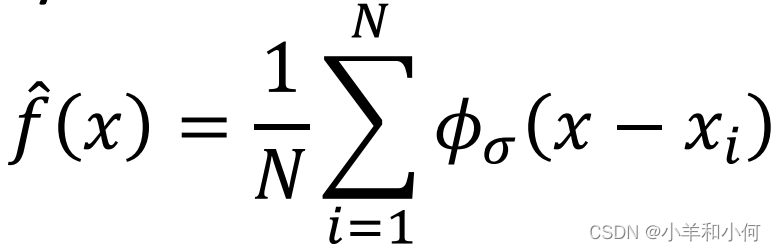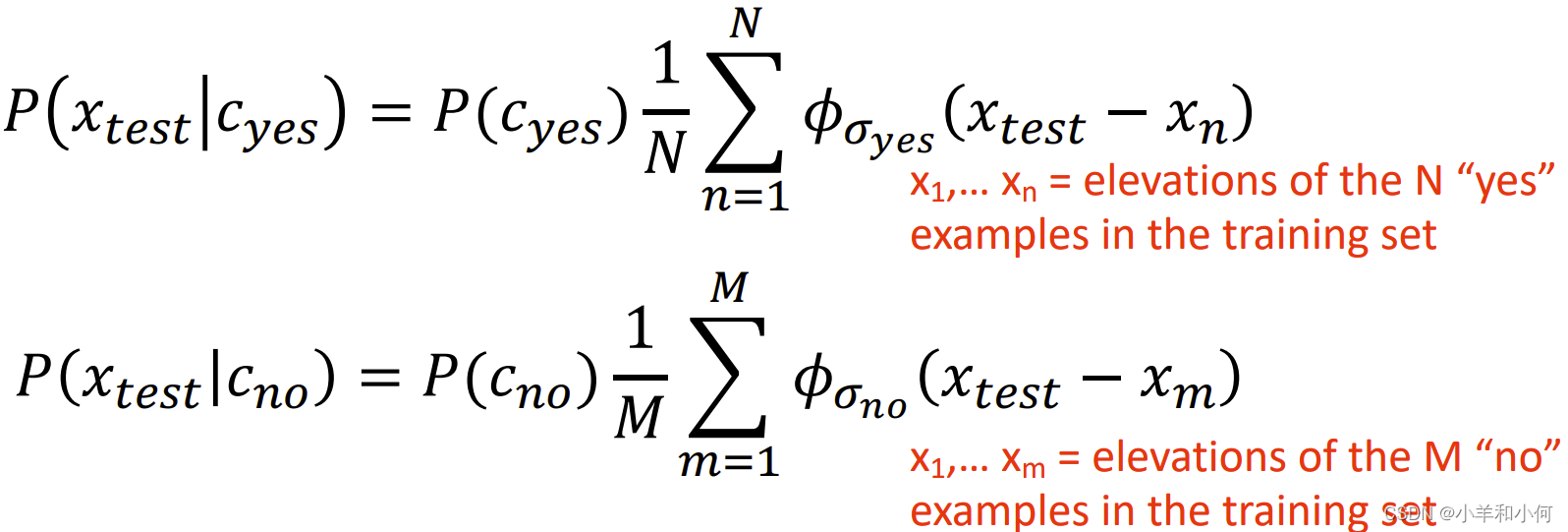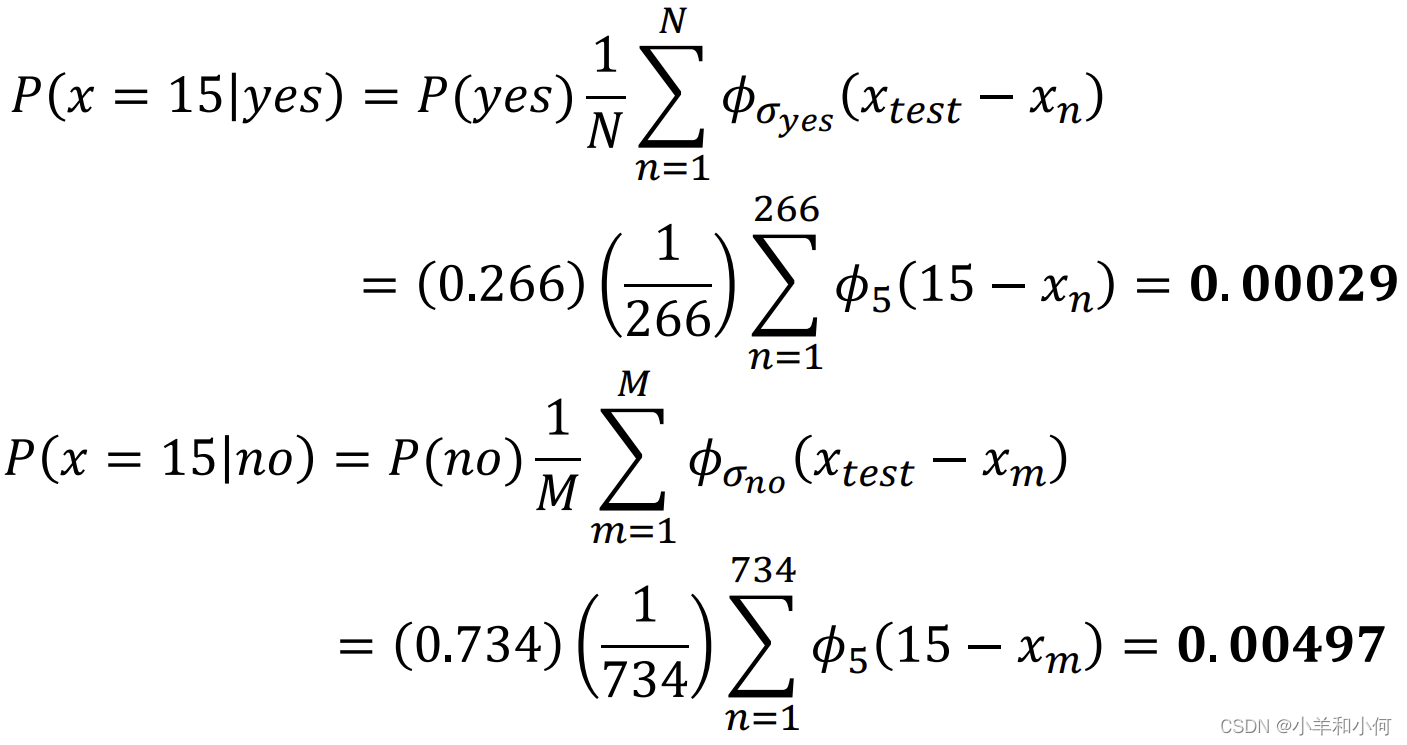| 机器学习基础:离散和连续数据 | 您所在的位置:网站首页 › 离散变量和连续变量的举例 › 机器学习基础:离散和连续数据 |
机器学习基础:离散和连续数据
|
目录 1. 连续的属性 2. 连续变量中的贝叶斯公式 2.1 上述方法的局限 3. 高斯贝叶斯 4. KDE 核密度估计 5. 贝叶斯的种类 1. 连续的属性首先回顾一下朴素贝叶斯的公式:
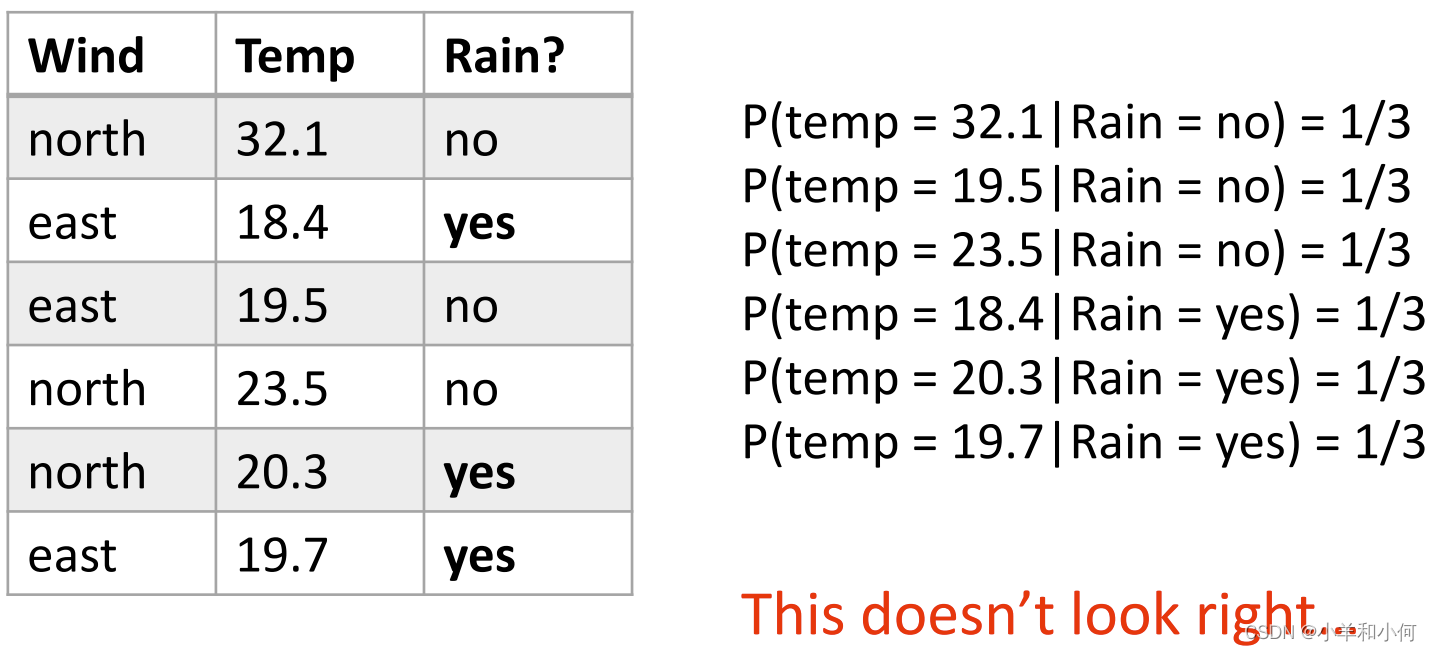
连续变量中
对于连续的属性,我们不能对单个属性值计算概率。比如上面我们得到的概率值全部为
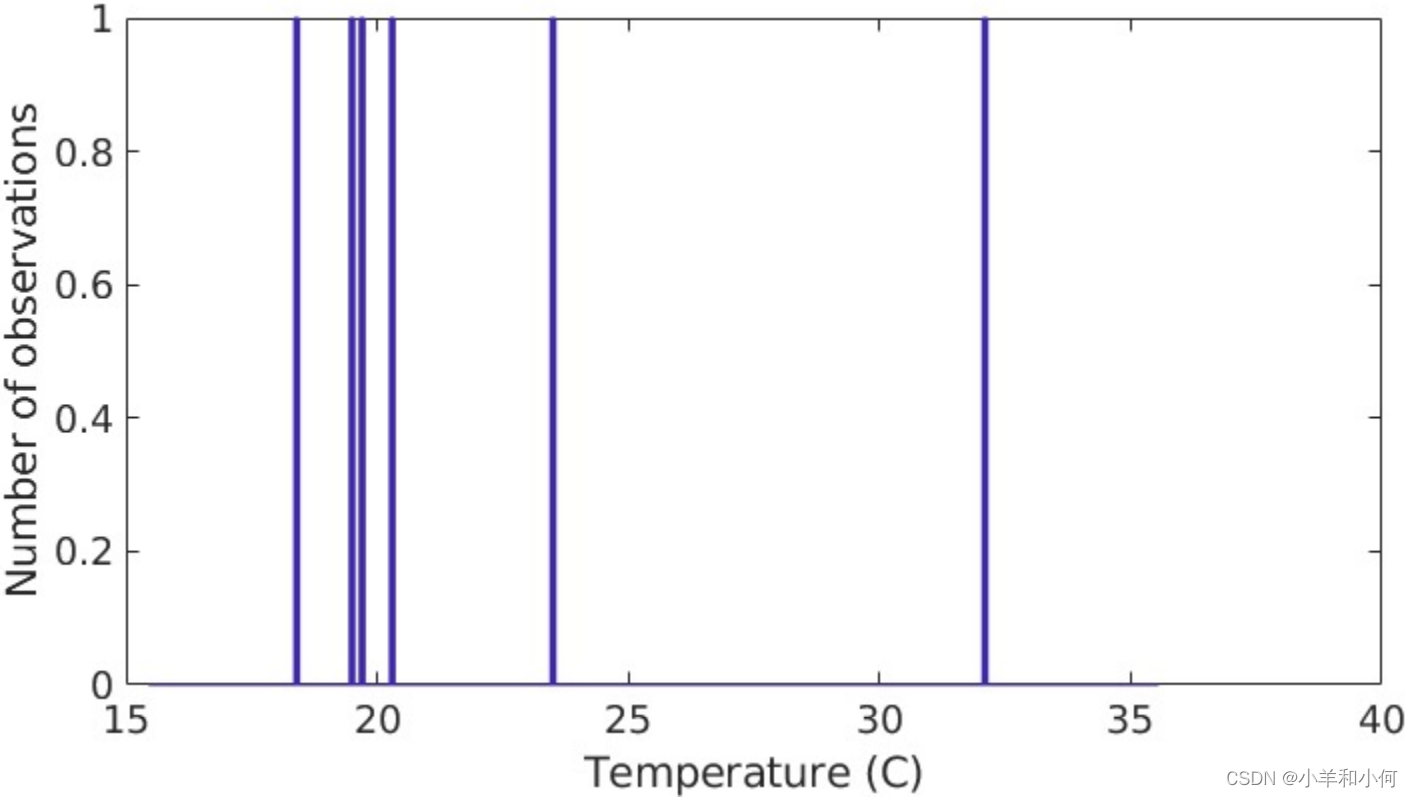
通过上图我们发现,数据的分布并不是均匀的,而是在 通过将连续的变量分入不同的
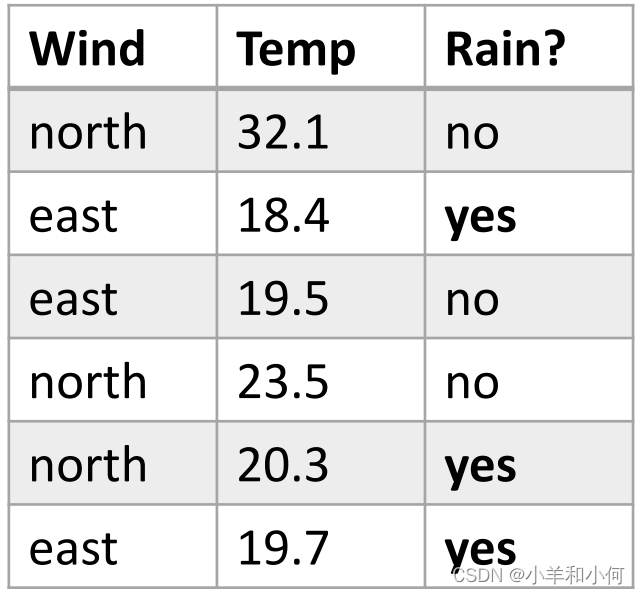
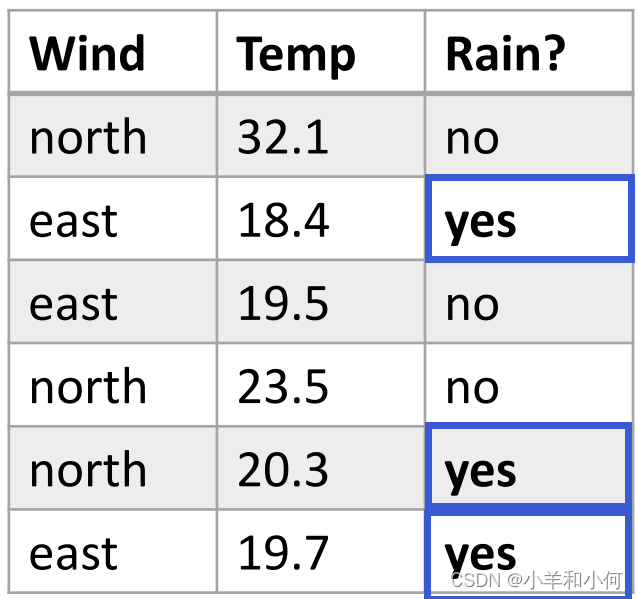
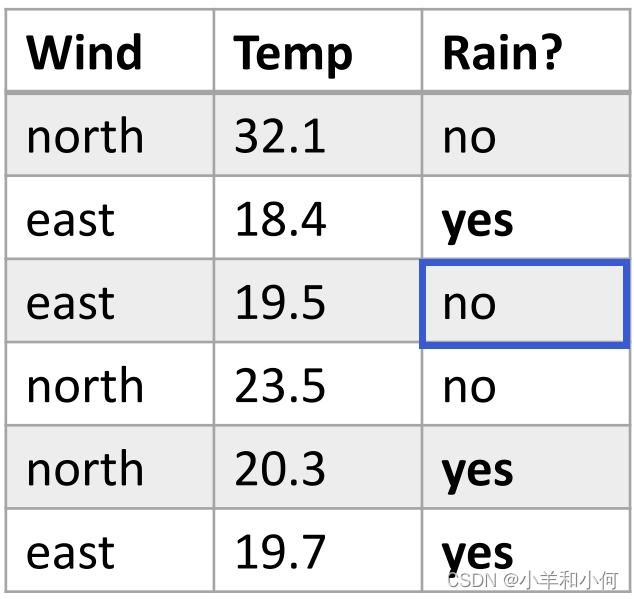
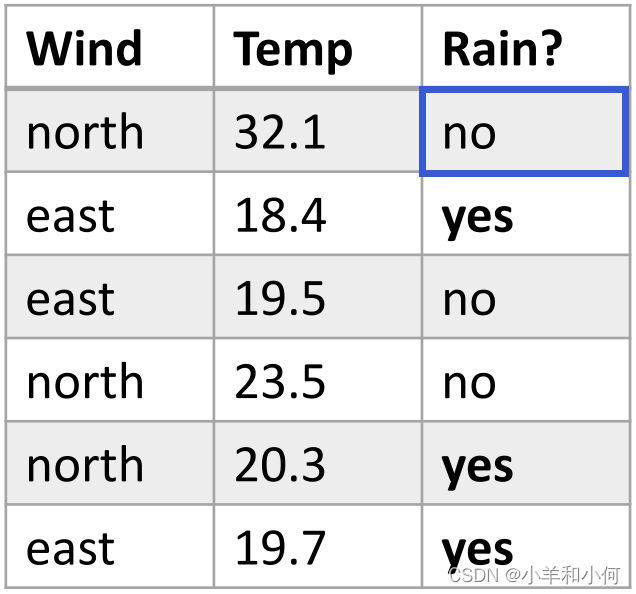
可以分不同的 还是上面天气的例子:
我们现在已经知道如何把
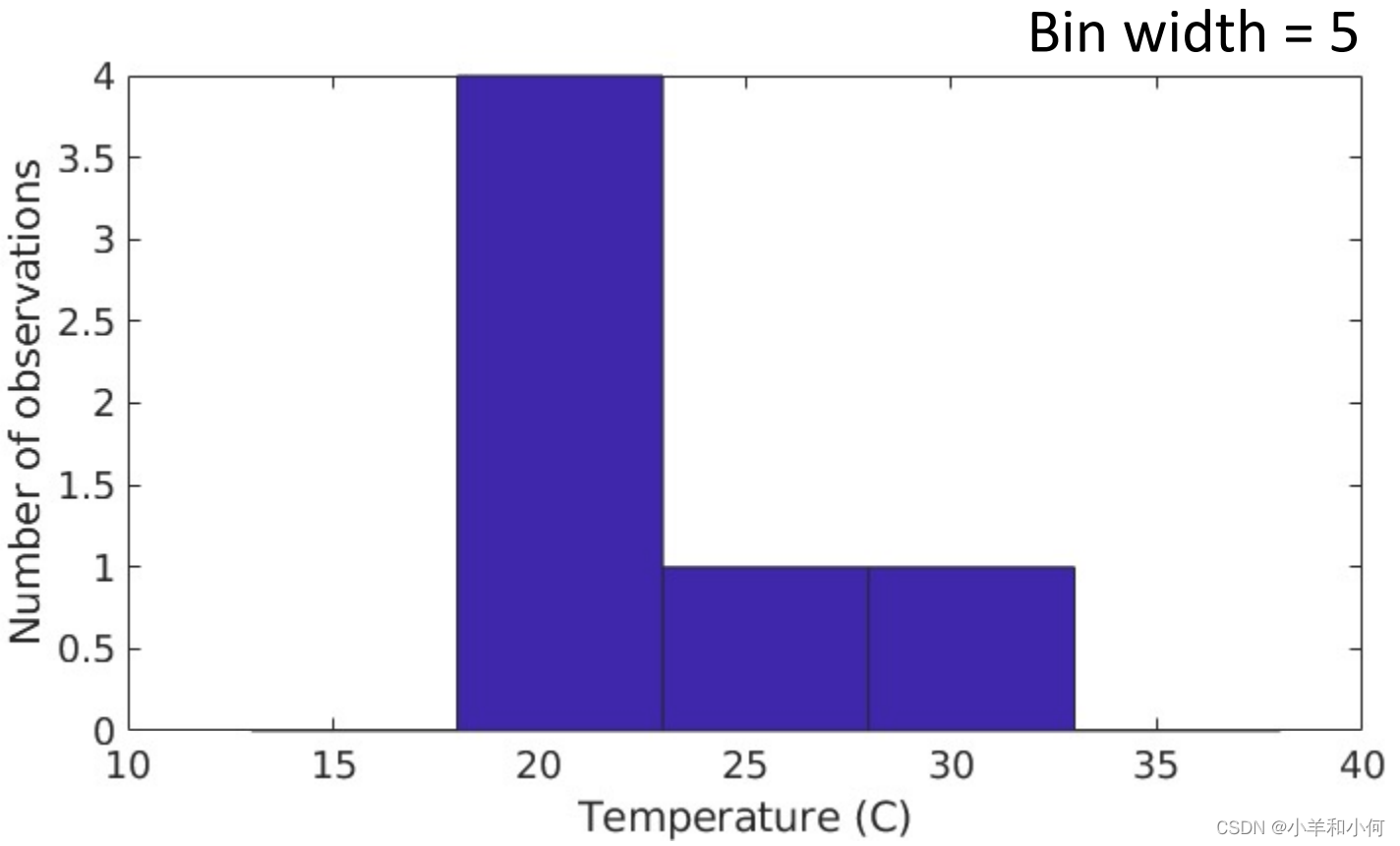
如果按照下图的方法划分:
则 分 当数据量不大的情况下,可能数据的分布并不能够与数据量大的时候保持一致,换句话说,通过少量数据得到的分布并不具有代表性。 那么常用的解决思路是什么呢? 3. 高斯贝叶斯引入高斯分布来代替连续数据的概率分布。之所以这样做,是因为在很多的自然条件下,随机变量的分布都会趋向于高斯分布。因此高斯分布经常被用在连续变量的分布中作为概率分布的假设。
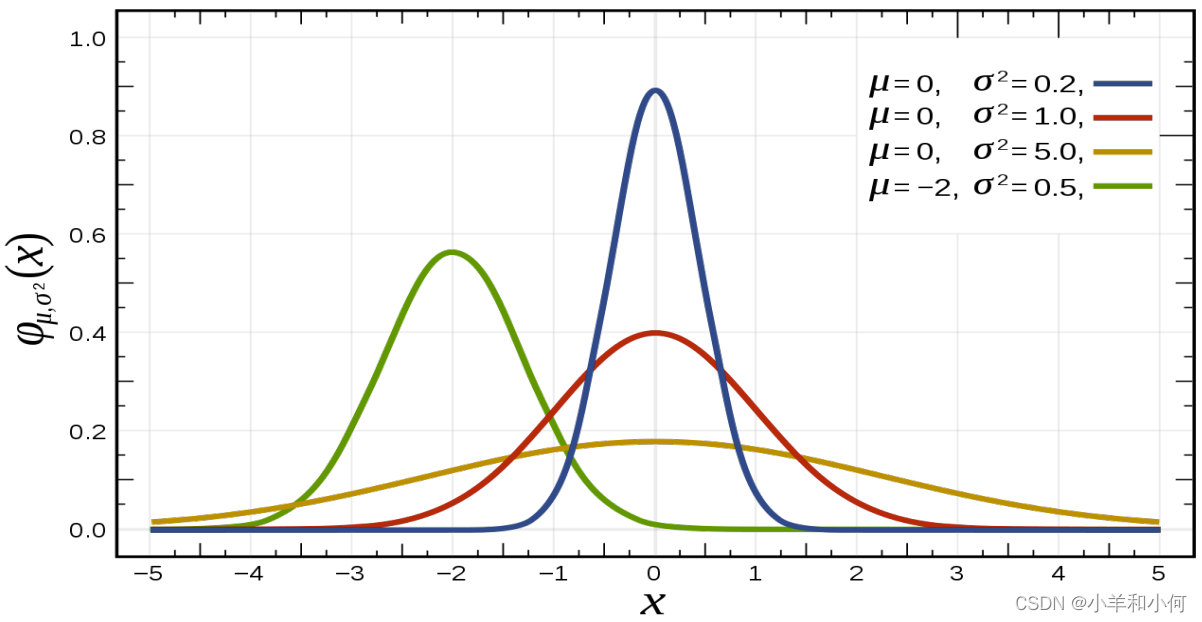
由一个具有平均值(期望值)
概率密度函数:
曲线下的面积为 均值 一个属性
一个属性
这里的标准差计算时,分母之所以采用 根据
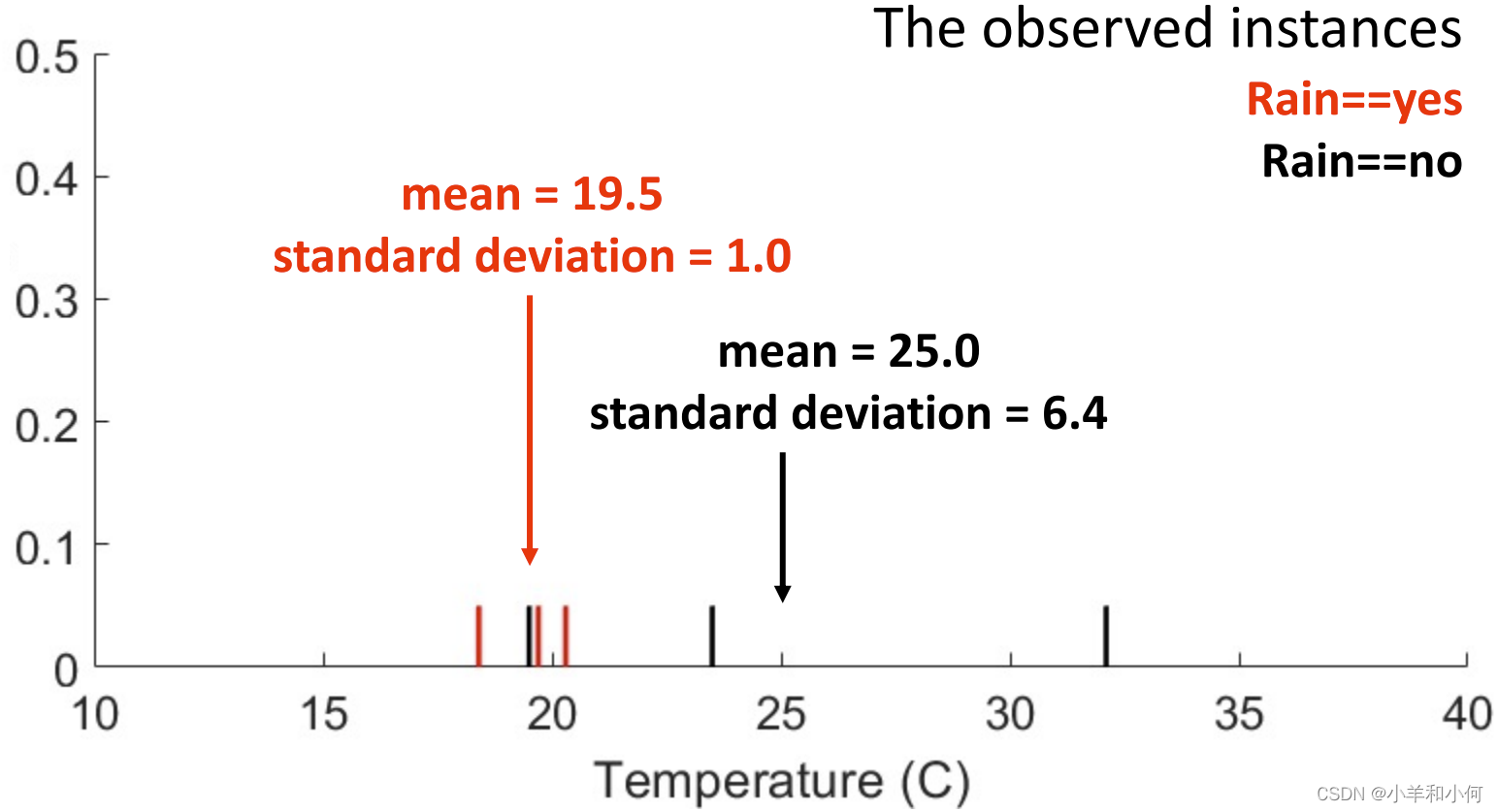
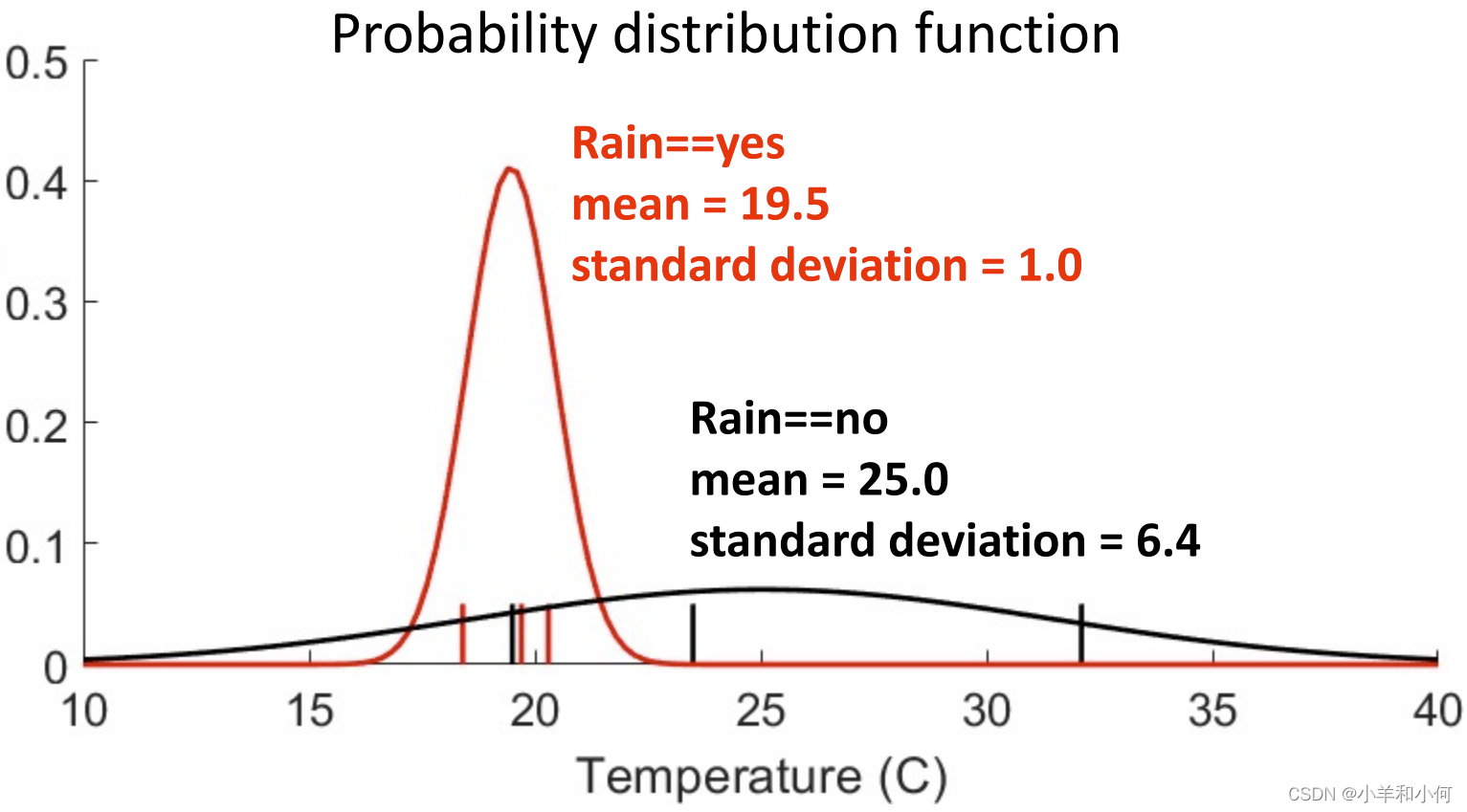
同样的我们也可以算出
然后我们分别把
这个图的纵轴代表的是什么呢?代表的是
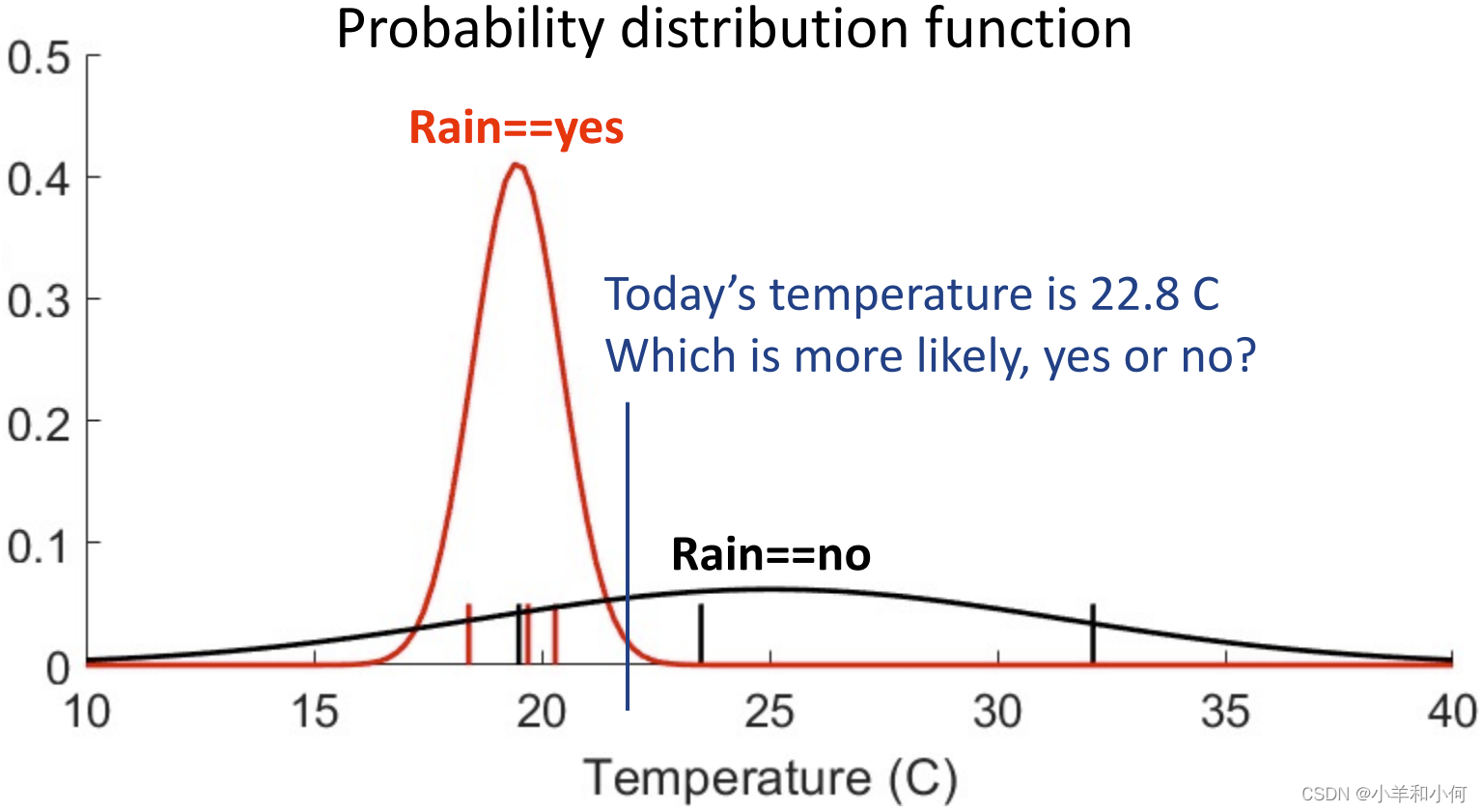
例如我们拿到一个
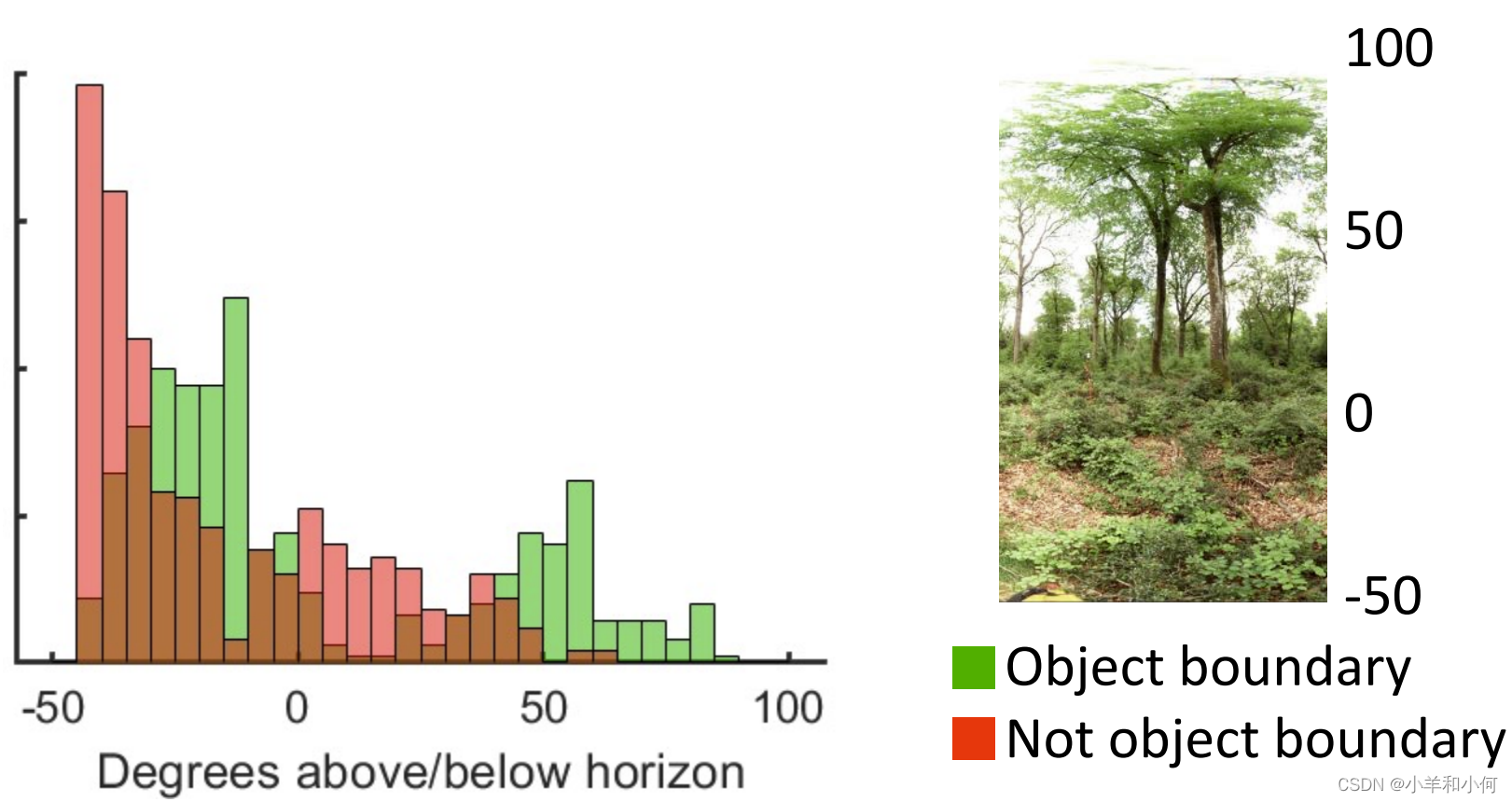
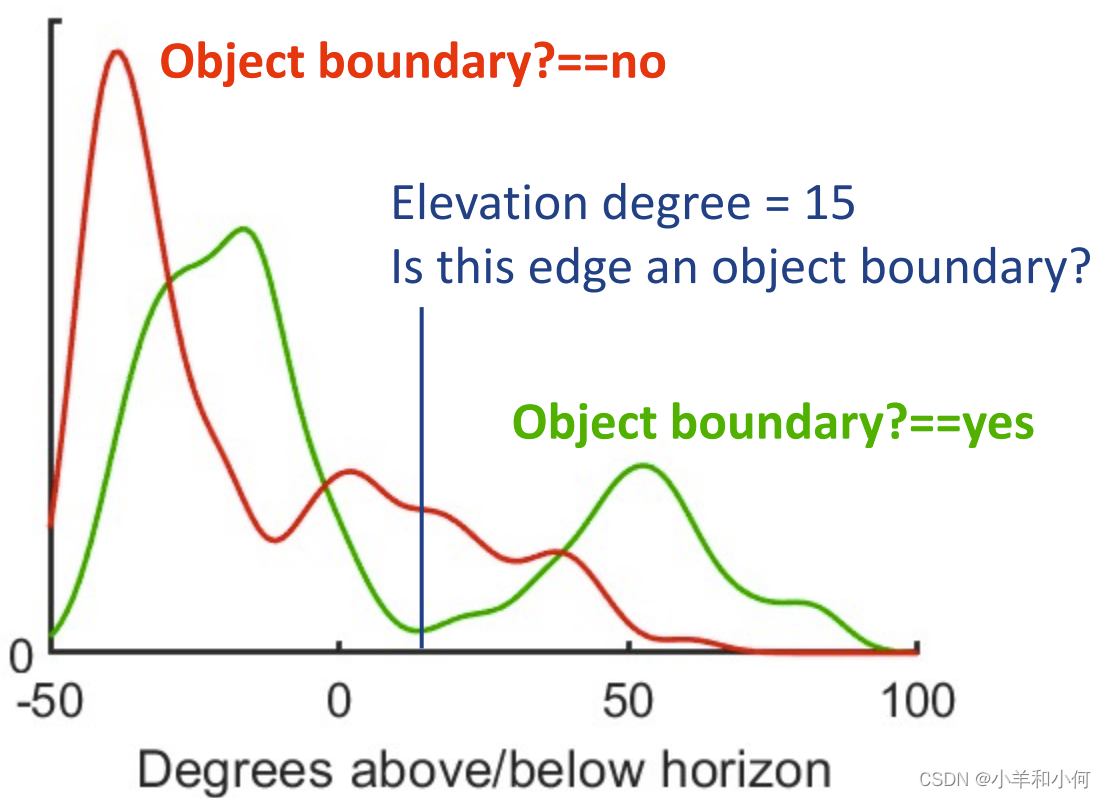
根据最终的结果,我们可以得出结论:22.8℃的时候,不下雨的概率大。 4. KDE 核密度估计并不是所有的概率分布都满足高斯分布:
这种情况下,我们采用 KDE 方法来进行贝叶斯概率计算:
其中,
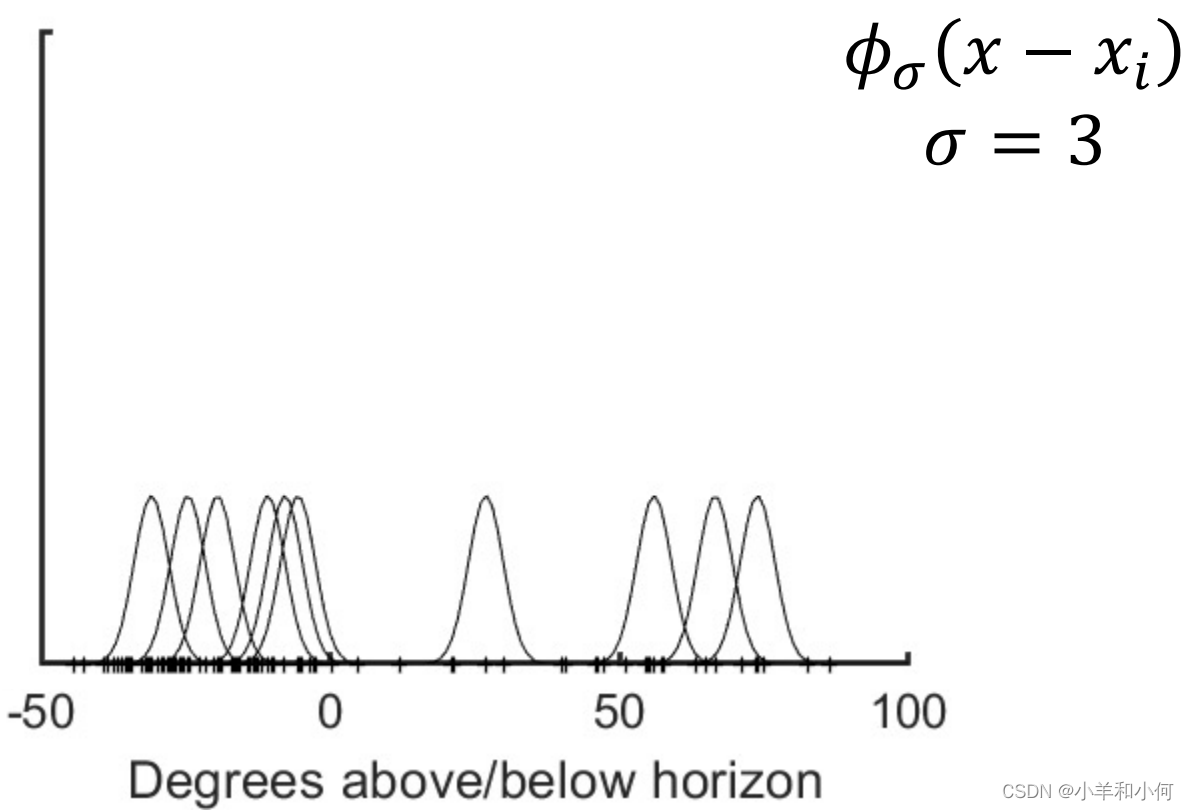
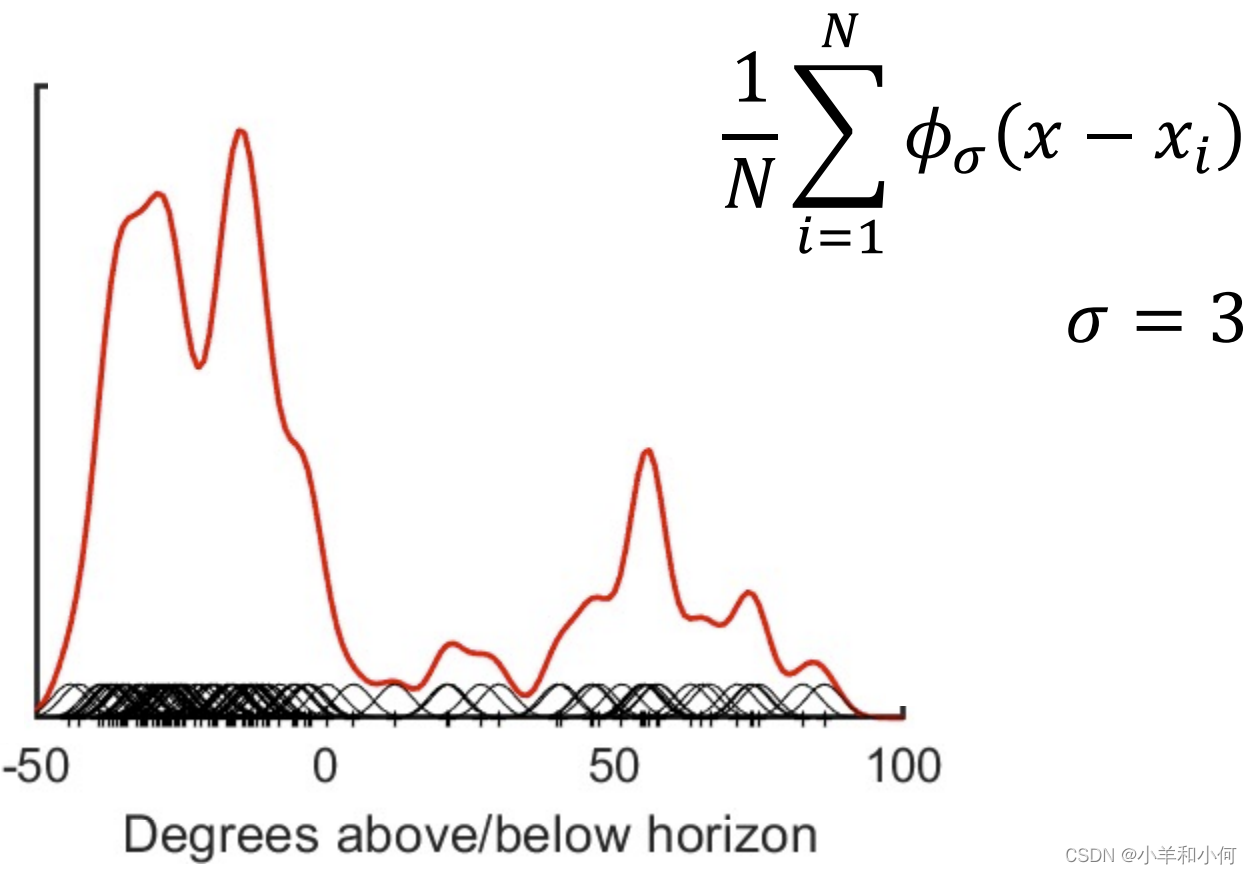
假设现在有一个 将给出的
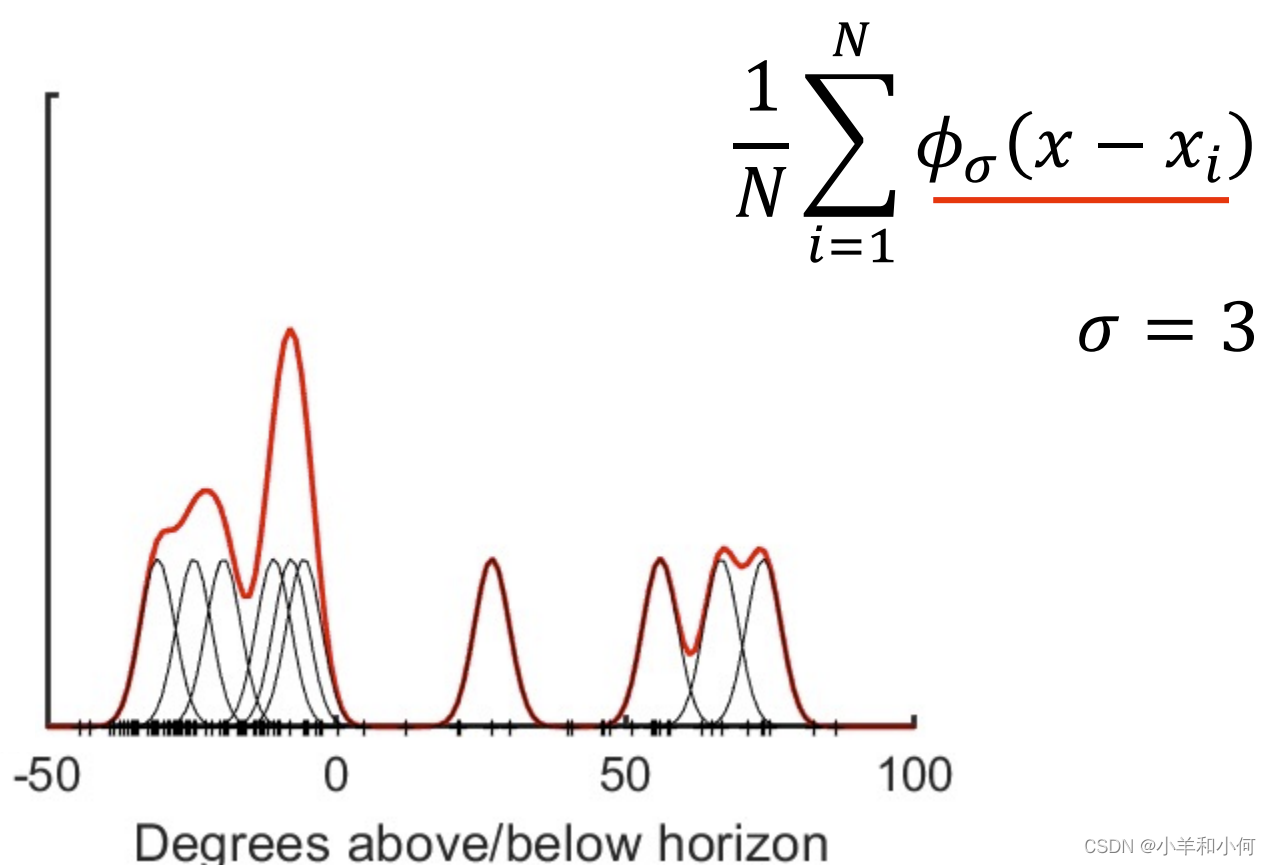
这个 这样当 最终按照公式进行叠加,可以得到下图中的红色线,就是真正的概率密度曲线:
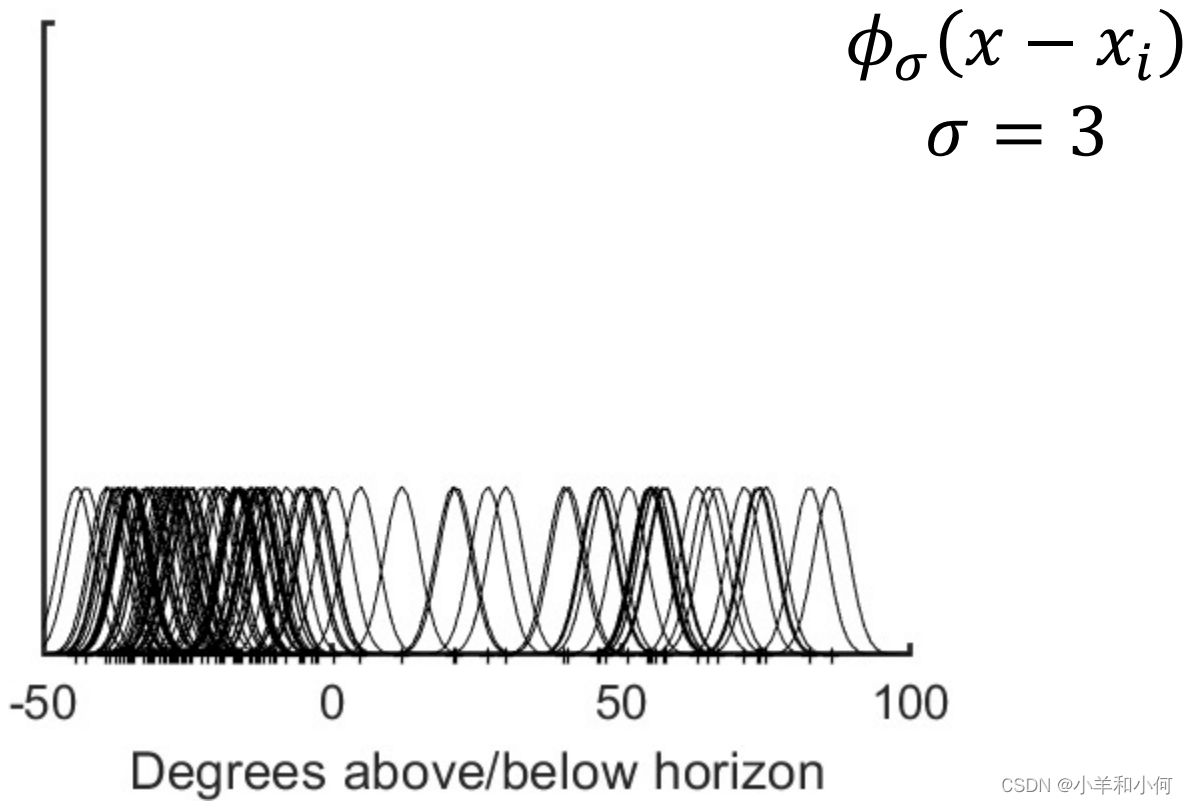
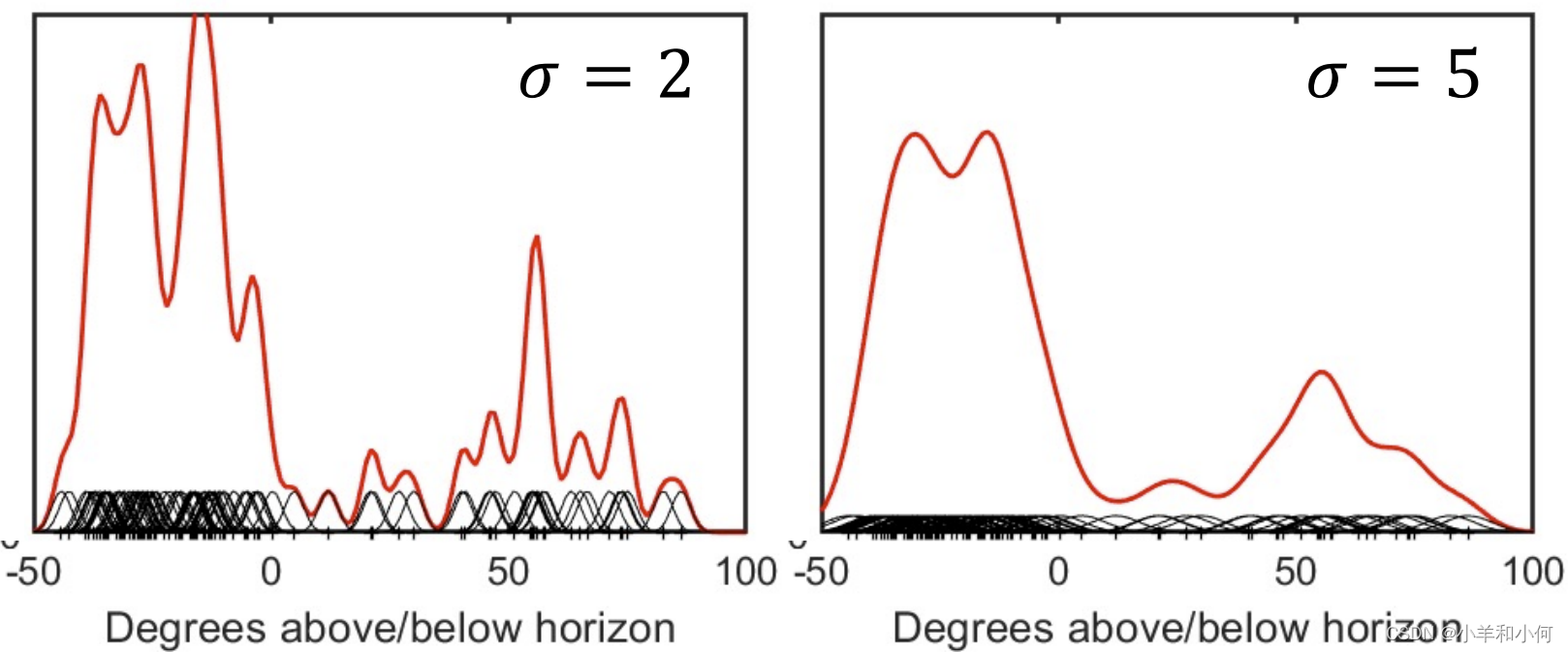
KDE:内核宽度 KDE有一个参数:高斯的标准偏差 参数必须由用户选择。
当指定一个具体的值,例如
优势 可以建立任意概率分布模型。没有关于分布形状的假设 (例如高斯分布)。劣势 需要选择一个内核带宽多变量(Multivariate):属性是象征性的,可以取固定数量的任何值。 二项式(或伯努利式)【Binomial (or Bernoulli)】:属性是二进制的。 多变量的特殊情况多项式(Multinomial):属性是对应于频率的自然数。 高斯(Gaussian):属性是数字的,我们可以假设它们来自高斯分布。 核心密度估计(Kernel density estimation):属性是数字,来自一个任意的分布。 |
【本文地址】