| 一种基于矩阵等价的布尔函数仿射等价判定方法与流程 | 您所在的位置:网站首页 › 矩阵等价的判定方法 › 一种基于矩阵等价的布尔函数仿射等价判定方法与流程 |
一种基于矩阵等价的布尔函数仿射等价判定方法与流程
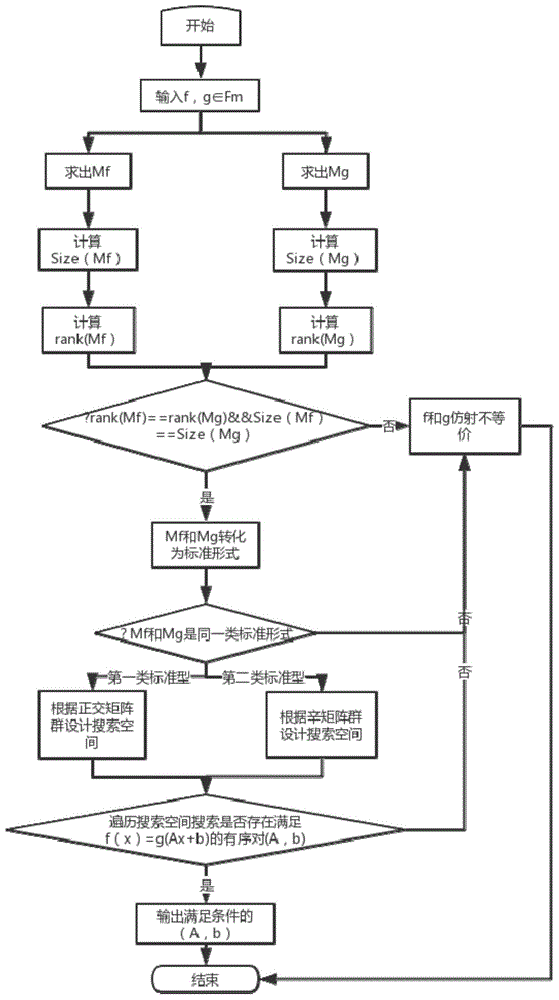 本发明属于数字集成电路与密码学的技术领域,具体涉及一种基于矩阵等价的布尔函数仿射等价判定方法。 背景技术: 两个布尔函数称为仿射等价(affineequivalence):若两个布尔函数f(x)和g(x)满足:g(x)=f(ax+b),其中:a为二元域f2上的非奇异矩阵,b是f2上的n维向量,则称f(x)与g(x)仿射等价,(a,b)称为一个仿射变换,所有的仿射变换构成的群称为仿射群,记为agl(n,2)。 布尔函数在计算机科学和现代密码学中发挥着重要作用。仿射等价作为布尔函数的基本等价,在组合电路设计中得到了广泛的应用,在密码学中也有很好的应用,例如reed-muller代码的陪集分类和分组密码。 在电路的应用中,n变量布尔函数表示一个电路,它接受n个输入(每个取值0或1),并产生单个输出(0或1)。如果两个布尔函数是仿射等价的,那么它们所代表的物理电路可以被认为是相同的。因此,有必要确定物理中布尔函数之间的等价类。通过计算布尔函数的仿射等价类,可以从本质上知道不同物理电路的数量。 在密码学的应用中,仿射等价性作为布尔函数之间的重要关系,因为布尔函数的许多密码属性在仿射变换后保持不变。仿射等价已成功用于旋转对称布尔函数的分类,bent函数的构造和reed-muller代码的分类。关于仿射布尔函数和reed-muller代码的陪集有一个事实:当布尔函数f和g是仿射等价时,它们也在reed-muller代码的相同陪集中。1972年,berlekamp和welch成功地将所有5变量布尔函数分类为48个等价类。1991年,maiorana通过将布尔函数分解为5变量函数,然后将该方法应用于5变量布尔函数,将所有6变量布尔函数分类为150357等价类。 除了仿射等价外,布尔函数还有一些更强的等价分类,如ccz等价、npn分类等。探索确定布尔函数仿射等价的方法,对这些等价决策也有帮助。 许多学者对布尔函数的仿射等价类进行了深入的研究,但如何确定两个给定布尔函数的等价性却鲜有研究,只有几篇论文在讨论这个问题。 2003年,jfuller和wmillan提出了一种检测布尔函数仿射等价性的方法,并应用该方法分析了s-box中的非线性。他们认识到对于两个仿射等价布尔函数f和g,f的1-局部邻域内的函数与g的1-局部邻域内的相应函数是仿射等价的,且仿射变换是相同的。f和g都有2n的连接函数,所以在同一个仿射变换下有2n+1对等价的布尔函数。他们主要利用这些信息以及代数程度、wht的绝对频率分布以及f和g的自相关函数来缩小仿射变换的搜索空间。值得注意的是,对于不同类型的布尔函数,复杂度相差很大。对于bent函数,这种方法很难确定仿射等价性。 2007年,孟还提出了一种检测布尔函数间仿射等价性的方法。在fuller方法的基础上引入导数函数和分解,得到了更多的约束条件,进一步降低了计算复杂度。 当函数是bent函数或真值表是稀疏的,这两种方法都不能确定仿射等价性,都需要大量的计算,因为wht的绝对分布只有几个候选项,自相关函数和代数程度也是如此。 技术实现要素: 本发明的目的在于针对现有技术中的上述不足,提供一种基于矩阵等价的布尔函数仿射等价判定方法,以解决或改善上述的问题。 为达到上述目的,本发明采取的技术方案是: 一种基于矩阵等价的布尔函数仿射等价判定方法,其包括: s1、对任意变量的两个布尔函数进行仿射等价判定; s2、根据布尔函数f2生成正交矩阵群和辛矩阵群,并得到正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元; s3、将所述正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元输入gap系统生成所有的正交矩阵、辛矩阵和非奇异矩阵,并通过遍历搜索空间得到布尔函数仿射等价中有序对(a,b)。 优选地,步骤s1具体包括: s1.1、根据布尔函数中真值表中包含不同个数1对其进行分类; s1.2、对含有m个1的布尔函数,记为fm,对使f取值为1所对应的变量取值xi构成on-set矩阵m; s1.3、计算任意两个布尔函数f,g∈fm的变量取值矩阵mf,mg,若f与g仿射等价,则size(mf)=size(mg),rank(mf)=rank(mg)=r; s1.4、分别将所述mf,mg转化为形如:或的标准型,其中,前者为第一类标准型,后者为第二类标准型; s1.5、若f与g仿射等价,则mf,mg的标准型为同一类,否则f与g必为非仿射等价。 优选地,步骤s2具体包括: 确定搜索空间其中d21是任意矩阵,d22是一个非奇异矩阵,当m被转化为第一类标准型时,d11∈正交矩阵群;当m被转化为第二类标准型时d11∈辛矩阵群。 优选地,步骤s3具体包括: 将所述正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元输入gap系统生成所有的正交矩阵、辛矩阵和非奇异矩阵,并通过遍历搜索空间d得到满足f(x)=g(ax+b)的有序对(a,b)。 优选地,将步骤s1、步骤s2和步骤s3应用于组合逻辑电路的方法包括: 组合逻辑电路的设计中,通过判断已经设计出电路c1所对应的布尔函数f1是否与需要实现的逻辑功能对应的布尔函数f2仿射等价,若仿射等价,则对电路c1的输入单元做适当线性组合,则可用c1来实现布尔函数f2。 优选地,将步骤s1、步骤s2和步骤s3应用于fpga可编程逻辑阵列的方法包括: 对基本逻辑单元的查找表的输入门进行线性组合,得到新的基本逻辑单元,增加fpga实现的功能,丰富fpga的设计。 优选地,将步骤s1、步骤s2和步骤s3应用于纠错编码的选取中,选出具有优良性质的纠错码,且通过缩小搜索空间,提高工作效率。 本发明提供的基于矩阵等价的布尔函数仿射等价判定方法,具有以下有益效果: 本发明不只是对部分的布尔函数进行仿射等价的判定,能够对含n个变量的布尔函数全体进行仿射等价的判定,并且能够对bent函数以及真值表稀疏函数进行有效判定。通过缩小搜索空间,极大地减小了对布尔函数仿射等价中有序对(a,b)求解的计算复杂度。 除此,本发明的布尔函数仿射等价的判定方法应用在组合逻辑电路和fpga的查找表中,可减少电路设计的工作量;应用于纠错编码的选取中,可选出具有优良性质的纠错码,且通过缩小搜索空间,可大幅度提高以上应用的工作效率。 附图说明 图1为本发明流程图。 具体实施方式 下面对本发明的具体实施方式进行描述,以便于本技术领域的技术人员理解本发明,但应该清楚,本发明不限于具体实施方式的范围,对本技术领域的普通技术人员来讲,只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内,这些变化是显而易见的,一切利用本发明构思的发明创造均在保护之列。 根据本申请的一个实施例,参考图1,本方案的基于矩阵等价的布尔函数仿射等价判定方法,包括: s1、对任意变量的两个布尔函数进行仿射等价判定; s2、根据布尔函数f2生成正交矩阵群和辛矩阵群,并得到正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元; s3、将所述正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元输入gap系统生成所有的正交矩阵、辛矩阵和非奇异矩阵,并通过遍历搜索空间得到布尔函数仿射等价中有序对(a,b); s4、将所述步骤s1、s2和s3应用于组合逻辑电路、fpga可编程逻辑阵列和纠错编码中。 根据本申请的一个实施例,以下将对上述步骤进行详细描述 s1、对任意变量的两个布尔函数进行仿射等价的判定,其具体步骤包括: 将布尔函数按照其真值表中包含不同个数1进行分类研究; 对含有m个1的布尔函数,记为fm,对使f取值为1所对应的变量取值xi构成on-set矩阵m,即:m=(x1,x2,...,xm)t,其中:f(xi1,xi2,...,xin)=1。 对任意两个布尔函数f,g∈fm,求出对应的变量取值矩阵mf,mg,若f与g仿射等价,则size(mf)=size(mg),rank(mf)=rank(mg)=r,这是判断两个布尔函数仿射等价的必要条件。 分别将mf,mg转化为形如:或的标准型,其中,前者为第一类标准型,后者为第二类标准型; 若f与g仿射等价,则mf,mg的标准型为同一类,否则f与g必为非仿射等价。 s2、根据布尔函数f2生成正交矩阵群和辛矩阵群,并得到正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元,利用正交矩阵群和辛矩阵群缩小搜索空间; 确定搜索空间其中d21是任意矩阵,d22是一个非奇异矩阵,特别的,当m被转化为第一类标准型时,d11∈正交矩阵群;当m被转化为第二类标准型时d11∈辛矩阵群。 s3、将所述正交矩阵生成元、辛矩阵生成元和非奇异矩阵生成元输入gap系统生成所有的正交矩阵、辛矩阵和非奇异矩阵,并通过遍历搜索空间得到满足f(x)=g(ax+b)的有序对(a,b)。 s4、将所述步骤s1、s2和s3应用于组合逻辑电路、fpga可编程逻辑阵列和纠错编码中。 其中,应用于组合逻辑电路中,在组合逻辑电路的设计中通过判断已经设计出电路(c1)所对应的布尔函数(f1)是否与需要实现的逻辑功能对应的布尔函数(f2)仿射等价,若仿射等价,我们可以对电路c1的输入单元做适当线性组合,就可以用c1来实现布尔函数(f2)。 在fpga的基本逻辑单元的应用中,可以对基本逻辑单元的查找表的输入门进行线性组合,得到新的基本逻辑单元,从而增加fpga实现的功能,丰富fpga的设计。 应用于纠错编码中,由于极大的缩小了搜索空间,可以更加快速地对reed-muller码进行仿射等价分析,可挑选出具有良好性质的纠错码。 根据本申请的一个实施例,设两个布尔函数f1,f2对应的on-set矩阵m1,m2秩相等且rank(m1)=rank(m2)=r,则存在b1,b2,p1,p2使得: 其中p1,p2是两个置换矩阵,b1,b2是两个非奇异矩阵。 若m1线性等效于m2,则存在置换矩阵p3,和非奇异矩阵b3,使得: 左乘其转置得: 由于式子(1)(2)的左边矩阵的12块和22块都是零矩阵。 把b3分为四块,即因此式子(4)就转化为: 只要找到满足式子(5)的b11,就可以将b3带入(3)去检查是否满足等式(3)。 如果找到满足式子(3)和(5)的b3,则可以得到: at=b1b3b2-1 其中,at为仿射等价参数; 现在问题等价于找到满足条件的b11,通过式子(5)知道,(ir+n1tn1)和(ir+n2tn2)必须是同一类标准形式,因此分两种情况计算搜索b11。 1)若存在非奇异矩阵b4,b5满足以下关系: 则属于第一类标准型。 将(6)(7)带入(5)得: 令d=d=b4-1b11b5,则(8)简化为: 将d分为与同样的四块: 显然要满足(9),则d11为正交矩阵,d12为0矩阵,d22是非奇异矩阵,d21为任意矩阵,d即是搜索空间。 2)若存在非奇异矩阵b6,b7满足以下关系: 则属于第二类标准型。 将(10)(11)带入(5)得: 令g=b6-1b11b7,则(12)简化为: 将g分为四块:g11是一个2h*2h的矩阵 那么(13)则转换为 g12=0(15) 因此,得出结论:g11是辛矩阵,g12是0矩阵,g21是任意矩阵,d22是非奇异矩阵,所有二元域上的2h*2h辛矩阵构成搜索空间。 本发明不只是对部分的布尔函数进行仿射等价的判定,能够对含n个变量的布尔函数全体进行仿射等价的判定,并且能够对bent函数以及真值表稀疏函数进行有效判定。通过缩小搜索空间,极大地减小了对布尔函数仿射等价中有序对(a,b)求解的计算复杂度。 除此,本发明的布尔函数仿射等价的判定方法应用在组合逻辑电路和fpga的查找表中,可减少电路设计的工作量;应用于纠错编码的选取中,可选出具有优良性质的纠错码,且通过缩小搜索空间,可大幅度提高以上应用的工作效率。 虽然结合附图对发明的具体实施方式进行了详细地描述,但不应理解为对本专利的保护范围的限定。在权利要求书所描述的范围内,本领域技术人员不经创造性劳动即可做出的各种修改和变形仍属本专利的保护范围。 |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |