| 【数学和算法】特征值、特征向量、特征空间,变换矩阵的行列式和特征值 | 您所在的位置:网站首页 › 矩阵特征向量之间的关系 › 【数学和算法】特征值、特征向量、特征空间,变换矩阵的行列式和特征值 |
【数学和算法】特征值、特征向量、特征空间,变换矩阵的行列式和特征值
|
可以参考马同学的博客: 如何理解矩阵特征值? 也可以参考B站小崔说数的视频教程:【线性代数的本质】特征值/特征向量的几何涵义 矩阵的特征值和特征向量定义:1、特征值是线性代数中的重要概念,设A是n阶方阵,如果存在数m和非零n维列向量x,使得Ax=mx成立,则称m是A的一个特征值或本征值。 2、非零n维列向量x称为矩阵A的属于特征值m的特征向量或本征向量,简称A的特征向量。 3、两种有着密切关系:属于不同特征值的特征向量一定线性无关,相似矩阵有相同的特征多项式,因而有相同的特征值。 先把结论写在前面: 矩阵特征值是对特征向量进行伸缩和旋转程度的度量。实数是只进行伸缩,虚数是只进行旋转,复数就是有伸缩也有旋转。其实最重要的是特征向量,从它的定义可以看出来,特征向量是在矩阵变换下只进行“规则”变换的向量,这个“规则”就是特征值。 矩阵特征值的几何含义:当特征值是实数时,特征值是拉伸倍数,特征向量是拉伸方向。 当特征值是复数时,就表示旋转90°。可用变换矩阵(0 -1 , 1 0)测试一下。 因为在复平面上,横轴表示实数,纵轴表示虚数,每乘上i就表示逆时针旋转90°,a+b*i乘上i变成了-b+a*i,在复平面图上画出来,很容易就看出来是逆时针旋转了90°。再乘上i就又旋转90°,就是180°,同时i²=-1,a+b*i就变成了-a-b*i,在图像上标出来,就容易看出来是旋转了180°。再旋转两次,就回到了最初的位置,因为i^4=1。 注意区分矩阵特征值与行列式代表的意义: 矩阵特征值表示在某一方向的拉伸倍数;而行列式表示在所以方向的拉伸倍数的乘积。因为矩阵A的行列式等于矩阵A的所有特征值相乘,这是相似矩阵的性质。由上面两条可知,二维变换矩阵的行列式就是面积伸缩倍数,三维变换矩阵的行列式就是体积伸缩倍数,以此类推…变换矩阵的特征值,表示某方向拉伸倍数。而n阶变换矩阵A的n个特征值组成的对角矩阵,和变换矩阵A相似。相似矩阵有个性质是,相似矩阵的行列式相等。所以可以求出变换矩阵的特征值后,使用 特征值组成的对角矩阵来看看各个方向的拉伸倍数。 下面记得区分旋转变换与拉伸变换 变换矩阵的行列式为0表示不可逆变换,不为0表示可逆变换。 对于旋转变换的话,旋转变换矩阵的行列式为1,因为只旋转不会拉伸,所以面积的拉伸倍数为1。行列式的几何意义就是面积变换的放大率; 但是行列式为1的矩阵不一定是旋转矩阵(注意这里没有限定是正交矩阵,所以不一定是旋转矩阵),只有当变换矩阵的四个元素满足正弦余弦,并且行列式为1的,才是旋转; 旋转矩阵都是行列式为1的正交矩阵。反之,行列式为1的正交矩阵也是一个旋转矩阵;(正交矩阵即逆为自身转置的矩阵) 变换矩阵正对角元素不为0,其他元素为0,表示拉伸,两个方向都拉伸。当某个正对角元素为1时,就表示该方向不拉伸; 变换矩阵副对角元素为±1,其他元素为0,表示顺或逆时针旋转90°。 两个矩阵M1和M2相乘的行列式等于两个行列式的乘积:
注意,二维变换矩阵的行列式为1,表示面积拉伸倍数一定为1(例如可能特征值为2和0.5,即在x方向拉伸2倍,在y方向拉伸0.5倍。当然,特征值也可能是3和0.333),并不一定表示旋转。 变换矩阵的特征值,才表示某方向拉伸倍数。而n阶变换矩阵A的n个特征值组成的对角矩阵,和变换矩阵A相似。相似矩阵有个性质是,相似矩阵的行列式相等。所以可以求出变换矩阵的特征值后,使用 特征值组成的对角矩阵来看看各个方向的拉伸倍数。 在刚体旋转时,由于已经确定就是旋转,所以旋转矩阵的行列式(可以证明旋转矩阵的各个特征值相乘为1)一定为1,就是正弦余弦的形式。 假设变换矩阵A的x,y特征值为2,3,那么点(x0,y0)经过矩阵A变换后就变成了(2*x0, 3*y0),即在x方向拉伸了2倍,在y方向拉伸了3倍。但这并不表示x,y的特征向量进行线性组合后也是特征向量。因为只有同一个特征值对应的特征向量进行线性组合才是特征向量。 每个特征值表示在特征向量方向上拉伸的倍数,所有三阶矩阵的特征向量并不是一样的,不是(1,0,0), (0,1,0),(0,0,1),而是像(1,3,0)之类的,特征值可能一样,也可能不一样,对某个特征值对应的特征向量进行线性组合就是该特征值对应特征向量的特征空间。 变换矩阵矩阵的某一个特征值所对应的特征向量的线性组合,依然是特征向量。如一个3阶矩阵A的特征值为2,3,4。那么特征值2满足A*(a,b,c)=2*(a,b,c),那么特征向量(a,b,c)可以为(1 0 0),也可以为(5 0 0),即 任意倍数*(1 0 0),同理,另外两个特征值对应的特征向量为任意倍数 *(0 1 0)和任意倍数 *(0 0 1)。 如一个3阶矩阵A的特征值2,2,4,那么特征值2 满足A*(a,b,c)=2*(a,b,c),那么特征向量(a,b,c)可以为(1,0,0)和(0,1,0),也可以为(9, 8, 0),即(a,b,c)满足线性组合为即任意倍数*(1 0 0)+ 任意倍数*(0 1 0),如(3,7,0)也是他的特征向量,因为A*(3,7,0)=2*(3,7,0),这个线性组合的特征向量就代表的是XOY平面内的所有向量,因为对该平面内的每个点做矩阵变换后,都会把这个点的x,y的值放大2倍。同理,另一个特征值4对应的特征向量的特征空间为任意倍数*(0 0 1),他却不能表示一个平面,因为他的前两维度必须为0,也就只是一条线,成不了一个面。 |
【本文地址】
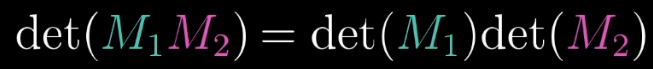 有的线性变换是可逆的,有的不行,比如行列式=0这样的线性变换就是不可逆的。从图像上看,图形会缩成一点,或者缩成一条直线,没有矩阵可以把它们恢复成原来的样子。
有的线性变换是可逆的,有的不行,比如行列式=0这样的线性变换就是不可逆的。从图像上看,图形会缩成一点,或者缩成一条直线,没有矩阵可以把它们恢复成原来的样子。