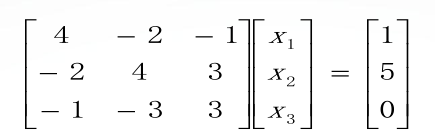matlab线性方程组求解

线性方程组的求解主要有两种方法，分别是直接法和迭代法，本节也将围绕这两种方法去讲解一些matlab在求解线性方程组的相关知识。 一、线性方程组的直接解法 主要可以分为以下三种方法： 高斯（ Gauss ）消去法 列主元消去法 矩阵的三角分解法 高斯（ Gauss ）消去法是一个经典的直接法，由它改进得到的列主元消去法，是目前计算机上求解线性方程组的标准算法，其特点就是通过消元将一般线性方程组的求解问题转化为三角方程组的求解问题。此外，还有矩阵的三角分解法等许多直接求解算法 。 1、利用左除运算符的直接解法 MATLAB 提供了一个左除运算符“\” 用于求解线性方程组，它使用列主元消去法，使用起来十分方便。对于线性方程组 Ax=b ，可以利用左除运算符反斜杠求解，b左除以A可获得线性方程组的数值解x。 注：这里的A和b是矩阵形式，且A里面的系数写法要与未知数对应。 例、用左除运算符求解下列线性方程组 。

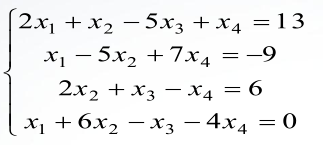
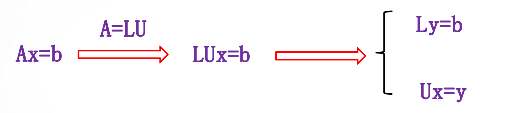2、利用矩阵分解求解线性方程组 矩阵分解是设计算法的重要技巧，是指将一个给定的矩阵分解成若干个特殊类型矩阵的乘积 ，从而将一个一般的矩阵计算问题转化为几个易求的特殊矩阵的计算问题 。通过矩阵分解方法求解线性方程组的优点是运算速度快，可以节省存储空间 。 下面将主要去讲解矩阵分解中的LU分解： （1） LU 分解的基本思想： 矩阵的 LU分解就是将一个n阶矩阵表示为一个下三角矩阵和一个上三角矩阵的乘积。线性代数中已经证明，只要方阵是非奇异的，LU 分解总是可以进行的。如下图 对于三角方程很容易求解，于是可以首先求解向量y使 Ly=b，再求解 Ux =y，从而达到求解线性方程组 Ax=b 的目的。 （2）matlab的LU分解函数 LU 分解函数是根据列主元LU分解算法定义的，具有较好的数据稳定性。 lu函数有两种调用格式： [L,U]= lu (A) ：产生一个上三角阵U和一个变换形式的下三角阵L，使之满足A=LU 。注意，这里的矩阵A必须是方阵。 [L,U,P]= lu (A) ：产生一个上三角阵U和一个下三角阵L以及一个置换矩阵P，使之满足 PA=LU 。同样，矩阵A必须是方阵。 注：当使用第一种格式时，矩阵L往往不是一个下三角阵，但可以通过行交换成为一个下三角阵。 还是以上述的线性方程组为例：

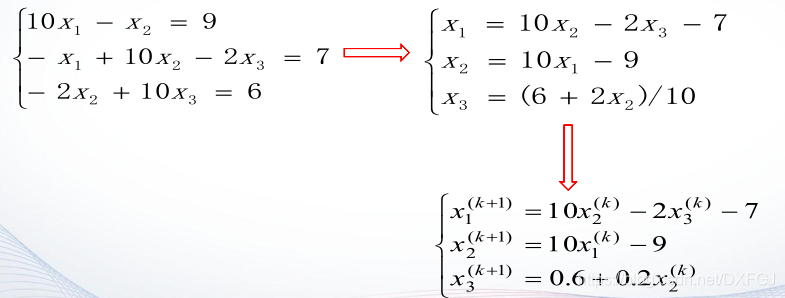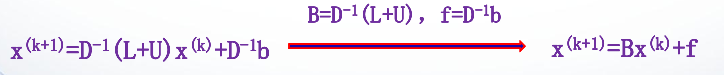一、 线性方程组的迭代解法 迭代法是一种不断用变量的原值推出它的新值的过程，是用计算机解决问题的一种基本方法 。如下面图片所示 介绍一种 线性方程组的迭代解法——雅可比（Jacobi）迭代法 对于线性方程组Ax=b，对于系数矩阵还是采取上述的矩阵分解的基本思想 求解公式为：x(k+1)=D(-1)*（L+U）*x(k)+D(-1)*b matlab中没有雅可比（Jacobi）迭代法的内置函数，因此此种方法需要自己编程实现，网上也有很多的代码，大家可以去了解一下，下面是网上的一段雅可比（Jacobi）迭代法的代码编写

其中，A是系数阵，b是方程组右边的常数，x0是迭代的初始值，ep是精度，在matlab 中将这段代码写入一个function，调用结果如下（以下面的方程组为例）:

可以看出两种方法算出来的结果，很是接近。 当然，除了此方法，还有很多的迭代方法去求解线性方程组，常见的有高斯- - 赛德尔（ Gauss- - Serdel ）迭代法，附上链接（https://blog.51cto.com/592669550/932010） 本节内容就到这里结束了，下节将推出非线性方程的求解，敬请期待！

关于MATLAB的学习：

大家可以关注我们的知乎专栏——数据可视化和数据分析中matlab的使用： https://zhuanlan.zhihu.com/c_1131568134137692160

欢迎大家加入我们的MATLAB学习交流群： 953314432 扫码关注我们 发现更多精彩