直线和平面所成的角

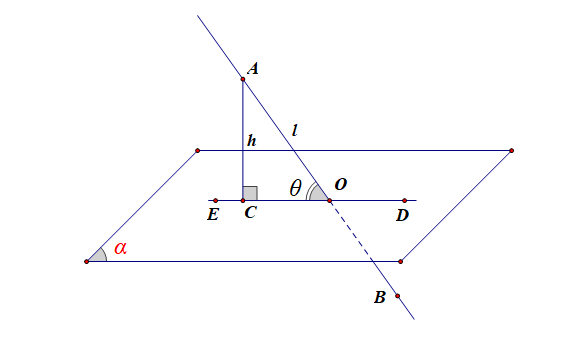
一般情形下的定义：如图所示，平面\(\alpha\)的一条斜线\(AB\)和它在平面上的射影\(DE\)所成的锐角\(\theta\)，叫做这条直线\(AB\)和这个平面\(\alpha\)所成的角。

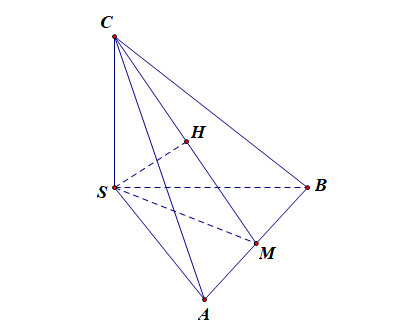
定义的补充：当一条直线垂直于平面，它们所成的角是直角；当一条直线和平面平行，或在平面内，它们所成的角是\(0^{\circ}\) 的角。

所以线面角范围：直线和平面所成角的范围是\([0°，90°]\)；

①直接法，由于线面角是平面的斜线与斜线在平面内的射影所成的角，故通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。举例如下：

四面体\(ABCS\)中，\(SA\)，\(SB\)，\(SC\) 两两垂直，\(∠SBA=45°\)，\(∠SBC=60°\)，\(M\)为\(AB\)的中点，求解：

(1). 直线\(BC\)与平面\(SAB\)所成的角。

分析：\(SC\perp SB\)，\(SC\perp SA\)，\(SC\perp\) 平面 \(SAB\)，

故\(SB\) 是斜线\(BC\) 在平面\(SAB\) 上的射影，

\(\angle SBC\) 是直线 \(BC\) 与平面 \(SAB\) 所成的角为\(60°\).

(2). 直线\(SC\)与平面\(ABC\)所成的角。

分析：连结\(SM\)， \(CM\)，则\(SM\perp AB\)，又\(SC\perp AB\)，

\(AB\perp\) 平面\(SCM\)，面\(ABC\perp\) 面\(SCM\)，过\(S\)作\(SH\perp CM\)于\(H\)，

则\(SH\perp\) 平面\(ABC\)，直线\(CH\)即为 \(SC\) 在面\(ABC\)内的射影。

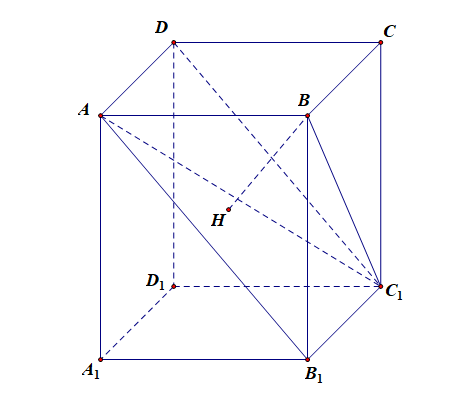
\(\angle SCH\) 为直线\(SC\)与平面\(ABC\)所成的角。令\(SB=2\)，则\(SA=2\)，\(SC=2\sqrt{3}\)，

\(AB=2AM=2\sqrt{2}\)，则\(AM=\sqrt{2}\)，\(SM=\sqrt{2}\)，则\(CM=\sqrt{14}\)，

在\(Rt\triangle SCM\)中，利用等面积法，可得\(SH=\cfrac{2\sqrt{3}}{\sqrt{7}}\)，由\(\sin\angle SCH=\cfrac{SH}{SC}\)，

可得，直线\(SC\) 与平面 \(ABC\) 所成的角的正弦值为\(\cfrac{\sqrt{7}}{7}\).

解后反思：①等面积法；②垂线段的相对性；③注意线面角的视角；

②利用公式\(\sin\theta=\cfrac{h}{l}\)求解，其中\(\theta\)是斜线与平面所成的角，\(h\)是垂线段的长，\(l\)是斜线段的长，其中求出垂线段的长(即斜线上的点到面的距离)既是关键又是难点，在具体题目中常使用构造三棱锥，利用等体积法来求垂线段的长。

长方体 \(ABCD-A_{1}B_{1}C_{1}D_{1}\)， \(AB=3\)， \(BC=2\)， \(A_{1}A=4\)， 求 \(AB\) 与面 \(AB_{1}C_{1}D\)所成的角的正弦值.

解析：本方法的优越性在于我们不一定要精确的做出来这个线面角，比如本题目我们不需要确定点\(B\)在平面\(AB_{1}C_{1}D\)上的垂足具体在哪里；

设点\(B\) 到平面 \(AB_{1}C_{1}D\)的距离为\(h\)，

由等体积法，可知\(V_{B-AB_{1}C_{1}}=V_{A-BB_{1}C_{1}}\)，即\(\cfrac{1}{3}S_{\Delta AB_{1}C_{1}}\cdot h=\cfrac{1}{3}S_{\Delta BB_{1}C_{1}}\cdot AB\)，

即\(\cfrac{1}{3}\times \cfrac{1}{2}\times 5\times 2\times h=\cfrac{1}{3}\times \cfrac{1}{2}\times 4\times 2\times 3\)，解得 \(h=\cfrac{12}{5}\)，

设 \(AB\) 与面 \(AB_{1}C_{1}D\) 所成的角为\(\theta\)，则\(\sin\theta=\cfrac{h}{AB}=\cfrac{4}{5}\).

内容：平面外的一条斜线和它在平面内的射影所成的锐角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角。

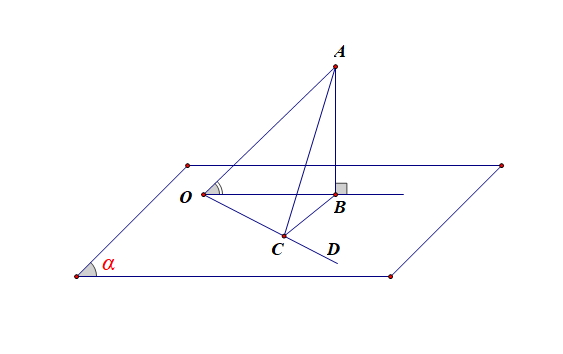
【证明】如图，\(AO\)是平面\(\alpha\)的斜线，\(AB\)是平面\(\alpha\)的垂线，

\(OB\)是斜线\(OA\)在平面\(\alpha\)内的射影，\(\angle AOB\)为锐角，

\(OD\)是平面\(\alpha\) 内和\(OB\)不重合的任一直线，在\(OD\)上截取\(OC=OB\)，

连结 \(AC\)，则 \(AB