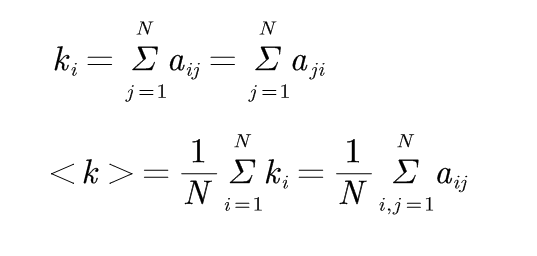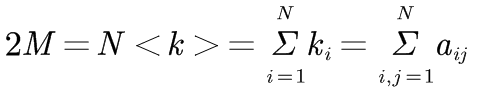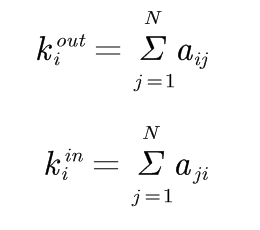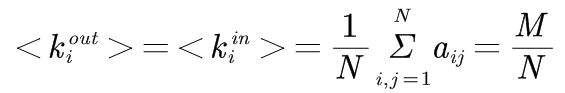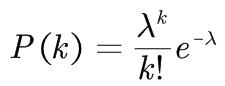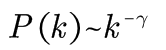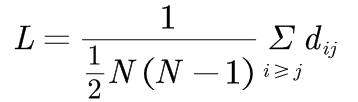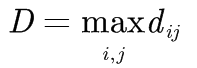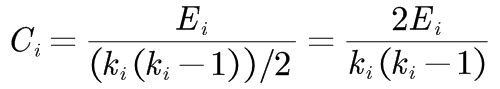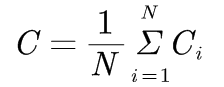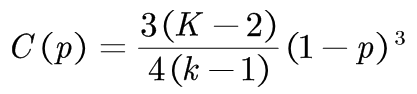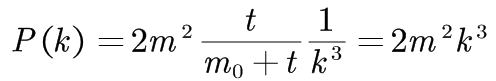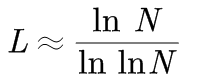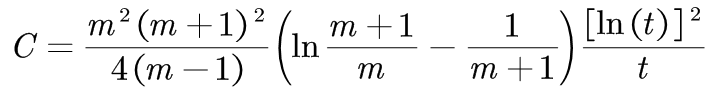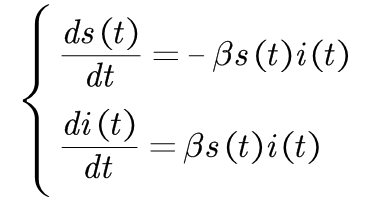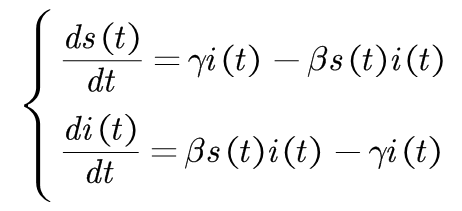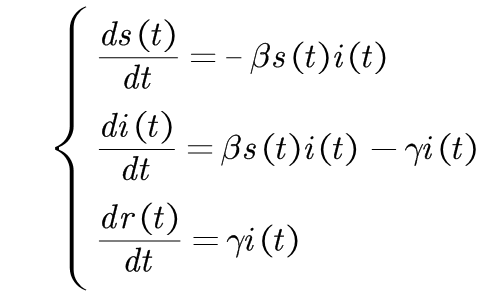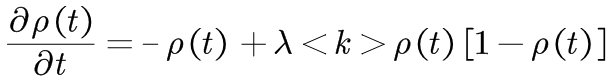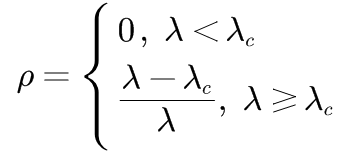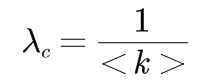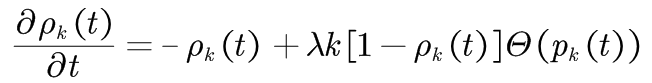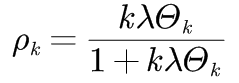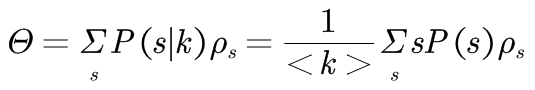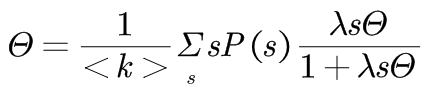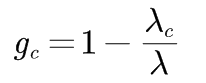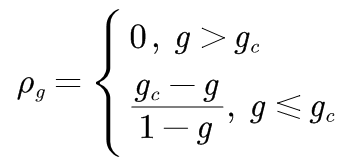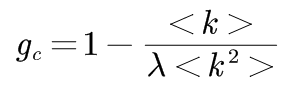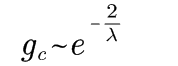复杂网络和传播动力学基本知识

写论文的理论基础吧，整理一下。

生活中网络随时可见，小到微博网络、游戏网络等等，大到金融网络、交通网络、电力网络、社交网络等等，这些种种的网络中都充满着复杂性，为研究其中的奥秘，利用网络科学理论进行刻画，往往会得到意想不到的结果。

在网络结构中，度是刻画单个结点属性的最简单但却最重要的概念之一。

在无向网络中，节点i的度ki定义为与节点直接相连的边的数目。无向网络中所有节点的度的平均值为平均度，记为< k >。

给定无向网络G中的邻接矩阵A=(aij)N×N，则有：

网络节点的度与网络边数M之间则有以下关系：

在有向网络中，节点的度包括出度和入度，有ki=kouti+kini。节点i的出度kouti指从节点i到其他节点的边的数目；入度kini指从其他节点到节点i的边的数目。它们可以通过邻接矩阵的元素表示：

有向网络中，网络的平均出度和平均入度相同，即有：

度分布是从统计概率角度观察网络结构特征的常用方式。

无向网络的度分布P(k)定义为网络中一个随机选择的节点的度为k的概率。

有向网络的出度分布P(kout)定义为网络中随机选择的一个节点的出度为kout的概率；入度分布P(k)in定义为网络中随机选择的一个节点的入度为kin的概率。

在复杂网络的模型中，通常将网络的度分布分为两类：泊松分布和幂律分布。

当网络度分布近似于泊松分布的网络时，该网络为均匀网络；当网络度分布近似于幂律分布的网络时，该网络为非均匀网络。

泊松分布满足：

幂律分布满足：

其中γ>0为幂指数，通常取值在2与3之间。

网络的平均路径长度L定义为任意两个节点之间的距离的平均值，即有：

其中，N为网络节点数。网络的平均路径长度又称为网络的特征路径长度或平均距离。

网络中任意两个节点之间的距离的最大值称为网络的直径，记为D，即有：

通常，在实际网络中，网络直径指任意两个存在有限距离的节点之间的距离的最大值。

“你的两个朋友也可能互为朋友”描述了人际关系的密切联系，可将这种属性定义为网络的聚类特性。

给定一个网络G，邻接矩阵A=(aij)N×N，节点i的度ki，节点i的聚类系数Ci，节点i的ki个邻居节点之间实际存在的边数Ei，则有：

将C定义为平均聚类系数，则有：

显然有0≤C≤1。C=0，当且仅当网络中所有节点的聚类系数均为0；C=1，当且仅当网络中所有节点的聚类系数均为1，此时网络为全局耦合的，即网络中任意两个节点都直接相连。

ER随机网络全称为 埃尔德什（Paul Erdos）- 雷尼(Alfred Renyi)随机网络。生成该网络的算法描述如下：

①从第N个孤立节点开始；

②选择一对节点，产生一个0-1之间的随机数。如果该随机数小于p，则这对节点之间放一条连接；否则，该节点对保持不连接；

③对所有N(N-1)/2个节点对重复步骤②。

ER随机网络如下所示：

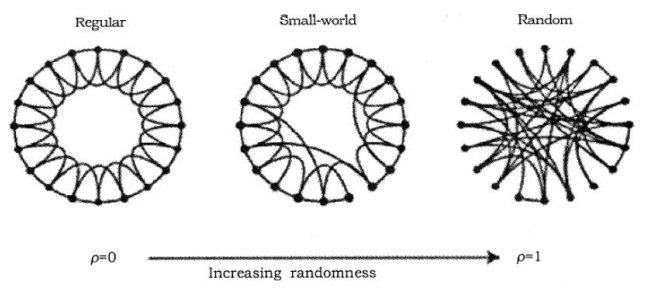
图中，包含N=50个节点，连边概率p=0.05。图中的颜色随节点度的变化而变化，度大的节点颜色深，度小的节点颜色浅。

1998 年，Watts 博士及 Strogatz 教授在《Nature》上发表《Collective dynamics of ’small-world’ networks》，由此提出了 WS 小世界网络模型。生成该网络的算法描述如下：

①从规则图构建：给定一个含有N个点的环状最近邻耦合网络，其中每个节点都与它左右相邻的各K/2个节点相连，K为偶数。

②随机化重连：以概率p随机地重新连接网络中原有的每条边，即把每条边的一个端点保持不变，另一个端点改取为网络中随机选择的一个节点。其中，规定任意两个节点之间不得有重边和自环。

综上，p=0对应于完全规则网络，p=1对应于完全随机网络，通过调节参数p的值就可以实现从规则网络到随机网络的过渡，如下图所示：

WS小世界网络模型如下所示：

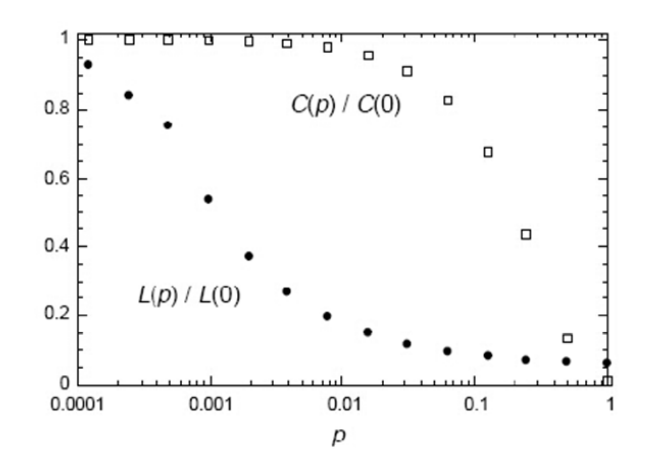
图中，包含N=50个节点，K=3，连边概率p=0.4。图中的颜色随节点度的变化而变化，度大的节点颜色深，度小的节点颜色浅。

WS 小世界的聚类系数 C(p)为：

WS 小世界网络的聚类系数和平均路径长度随重连概率的变化趋势如下：

由此，小世界特性指平均路径长度较小、而聚类系数较大。

Barabasi和Albert指出，ER随机图和WS小世界模型忽略了实际网络的两个重要特性，即增长特性（网络的规模是不断扩大的）和优先连接特性（新的节点更倾向于与那些具有较高连接度的hub节点相连接），故提出无标度网络模型。生成该网络的算法描述如下：

①增长：从一个具有m0个节点的连通网络开始，每次引入一个新的节点并且连到m个已存在的节点上，这里m≤m0

②优先连接：一个新结点与一个已经存在的节点i相连接的概率∏i与节点i的度ki之间满足如下关系：∏i=ki/∑jkj (分母为网络中总的节点度)

BA无标度网络模型如下所示：

图中，包含N=100个节点。颜色随节点度的变化而变化，度大的节点颜色深，度小的节点颜色浅。

若一个 BA 无标度网络含有 N 个节点，其度分布符合（显然具有幂律分布特点）：

平均路径长度：

聚类系数：

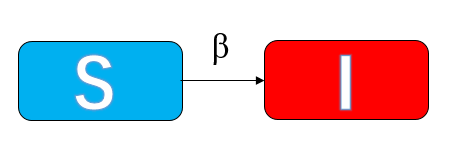
从聚类系数与平均路径长度中可知，当节点数渐渐增多时，BA 无标度网络的聚类特性并不明显，但具有小世界特性。

在经典的传染病模型中，种群(population)内的N个个体的状态可以分为如下几类：

SI模型中将人群分为两大状态：易感染状态S，感染状态I。这里记s(t)和i(t)为t时刻易感染人群和感染人群占整个人群数量的比例，且s(t)+i(t)=1。设每一个易感染个体在单位时间内与感染个体发生关联且被传染的概率为β。

SI模型图：

SI模型传播动力学方程：

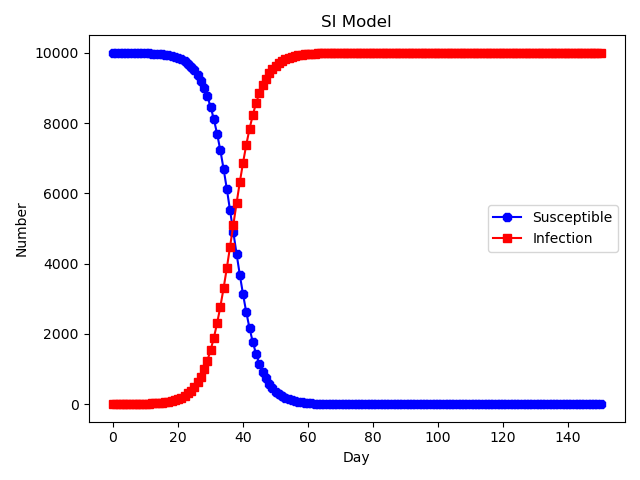
SI模型状态变化图：

可以看出，易染人群的数量处于递减的状态，而感染人群的数量处于增长的状态。

SIS模型中将人群分为两大状态：易感染状态S，感染状态I。这里记s(t)和i(t)为t时刻易感染人群和感染人群占整个人群数量的比例，且s(t)+i(t)=1。设每一个易感染个体在单位时间内与感染个体发生关联且被传染的概率为β；每一个感染个体以定长速率γ再变为易感染个体。

SIS模型图：

SIS模型传播动力学方程：

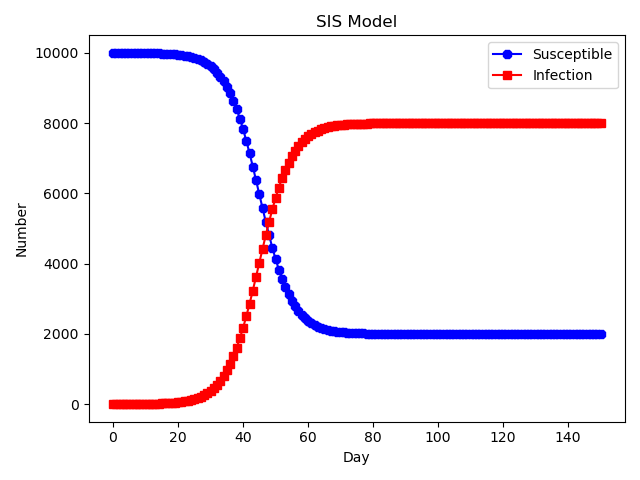
SIS模型状态变化图：

可以看出，随着时间的推移，两种状态的人群会保持成为一种稳定状态。

SIS模型中将人群分为两大状态：易感染状态S，感染状态I，免疫状态R。这里记s(t)、i(t)和r(t)为t时刻易感染人群、感染人群和免疫人群占整个人群数量的比例，且s(t)+i(t)+r(t)=1。设每一个易感染个体在单位时间内与感染个体发生关联且被传染的概率为β；每一个感染个体以定长速率γ再变为易感染个体。

SIR模型图：

SIR模型传播动力学方程：

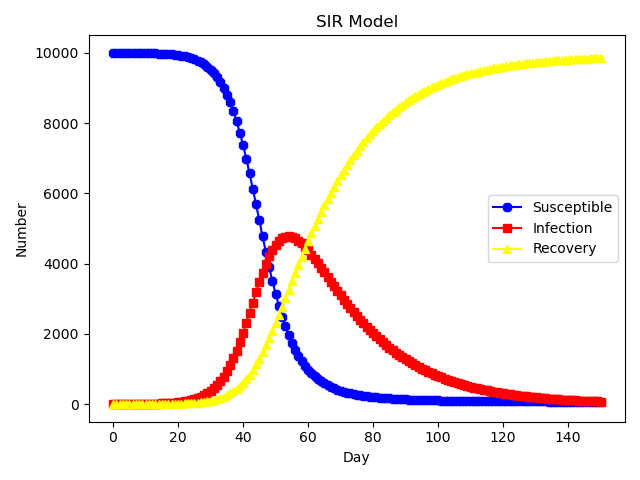
SIR模型状态变化图：

可以看出，在传播初期，三种状态个体密度并无大的变化；但随着时间的推移，易感态个体密度迅速下降，直到易感态个体密度为 0；而感染态密度迅速渐上升。当易感态个体密度为 0 时，感染态密度达到最大值。感染态密度增长的过程中，有部分感染态个体以概率γ恢复为免疫态个体。当感染态密度达到最大值后，群体中只存在这两种状态：感染态，免疫态。随着时间的推移，所有的感染态个体转变为免疫态个体。

如果一个易染节点的邻居节点中至少有一个感染节点，该节点被感染的概率设为常数β，而一个感染节点恢复到易染节点的概率假设为常数γ。则定义有效传播率λ=β/γ。一般地，可假设γ=1，因为这只会影响疾病传播的时间尺度。

现在，令p(t)为时刻t感染个体密度，当时间t趋于无穷大时，感染个体的稳态密度记为ρ。均匀网络(如ER随机图和WS小世界网络)的度分布在网络平均度< k >处有个尖峰，而当k 和 k >> < k >时指数下降，因而我们假设均匀网络中每个节点的度ki都近似等于< k >。基于平均场理论，当网络规模趋于无穷大时，通过忽略不同节点之间的度相关性，可得反应方程：

令上式右端为0，可以求得感染个体的稳态密度ρ如下：

其中，传播临界值为:

在均匀网络中，存在一个有限的正的传播临界值λc：当传播率λλc，则感染个体能够将病毒传播扩散并使得整个网络感染个体总数最终稳定于某一平衡状态。

在均匀网络中，假设每个节点的度都近似等于网络平均度< k >。而在非均匀网络中，节点度具有明显的区别，此时需要对不同度值的节点作不同处理。令相对密度ρk(t)为度为k的节点被感染的概率。基于平均场理论，得平均场方程为：

令上式右端为0，可得ρk(t)的稳态值ρk：

这表明节点的度越高，被感染概率越高。由于网络的非均匀性，对于度不相关的网络，由于任意一条给定的边连接到度为s的节点的概率为P(s|k)=sP(s)/< k >，可以求得：

综上，即得：

上式中，有一个平凡解θ=0。传播临界值λc必须满足：λc 趋近于无穷大，从而导致传播临界值λc趋近于零，故而非均匀网络几乎无传播阈值，病毒会在很短的时间内传播至全网。

选择合适的免疫策略对于传染病的预防和控制极为重要。

随机免疫方法是完全随机地选取网络中的一部分节点进行免疫，它可以用作检验其他有针对性设计的免疫方法的效果的基准。定义免疫节点密度为g，由平均场理论，随机免疫相当于把传播率从λ缩减为λ(1-g)。

对于均匀网络，

随机免疫对应的免疫密度临界值gc为

对应的稳态感染密度ρg为

对于非均匀网络，如无标度网络，随机免疫的免疫密度临界值gc为

当< k2 > →∞时，免疫密度临界值gc趋于1。这解释了，如果对于大规模无标度网络采取随机免疫策略，需要对网络中几乎所有节点都实施免疫才能最终消灭病毒传染。

目标免疫就是希望通过有选择地对少量关键节点进行免疫以获得尽可能好的免疫效果。然而对于均匀网络，网络内的节点具有同质性，网络连通性较高，即便是网络中一部分节点被免疫，病毒依然可以通过其他未免疫节点传播至全网。由于在无标度网络上的传播阈值趋近于零，随机免疫策略会在无标度网络上失效，因此该免疫策略是针对无标度网络提出，在现实世界中，无标度性质更为广泛。在无标度网络上，可以选取度大的节点进行免疫。而这一些节点被免疫后，意味着这些节点在病毒传播网络中被移除，网络被分裂为碎片，使得病毒的传播存在有限的临界阈值，从而帮助人们消灭传染病。

在无标度网络中，目标免疫的免疫临界值gc满足

可以看出，即使传播率λ在很大的范围内取不同的值，都可以得到很小的免疫密度临界值。因此，有选择地对无标度网络进行目标免疫，其临界值要比随机免疫情形小得多。

目标免疫需要了解网络的全局信息以来寻找并控制传染病传播的 hub 节点。然而对与庞大复杂的且不断演化的人类社会与Internet来说，无法从全局的角度找到这样的节点，这样做是非常难实现的。熟人免疫的基本策略是：从网络中选取 p 比例的个体进行免疫，再从被选择的个体中，随机选择他们邻居中的节点进行免疫。该免疫策略可以避免知道全局信息的问题，从局部的角度进行出发，只需知道被随机选择的节点以及与它们直接相连的邻居节点即可。

在无标度网络中，度大的节点表明有许多的节点与之相连；若随机选取一个节点，在选择其邻居时，度大的节点被选中的概率要高于度小的节点。因此熟人免疫策略的可操作性要高于目标免疫，且免疫效果要高于随机免疫。