| 2月20 高斯 | 您所在的位置:网站首页 › 牛顿迭代法怎么求收敛阶 › 2月20 高斯 |
2月20 高斯
|
文章目录
1.0高斯牛顿法1.1注意:1.1.1雅可比矩阵 Jacobian matrix1.1.2残差 residual,表示实际观测值与估计值(拟合值)之间的差1.2方法核心1.3 联合实际相机估计问题思考:1.4 保证算法收敛的机制1.5 效果优缺点分析1.5阻尼高斯牛顿法
2.0 LM方法matlab练习程序(高斯牛顿法最优化)
1.0高斯牛顿法
链接:https://blog.csdn.net/wuaini_1314/article/details/79562400 推导过程可以参考 http://blog.csdn.net/zhubaohua_bupt/article/details/74973347 http://fourier.eng.hmc.edu/e176/lectures/NM/node36.html http://blog.csdn.net/dsbatigol/article/details/12448627 1.1注意:高斯牛顿法解决非线性最小二乘问题的最基本方法,并且它只能处理二次函数。(使用时必须将目标函数转化为二次的) 参考:https://blog.csdn.net/jinshengtao/article/details/51615162 Unlike Newton’smethod, the Gauss–Newton algorithm can only be used to minimize a sum ofsquared function values 需要注意的是 高斯牛顿方法 在求解hessian matrix时 做了一个简化 高斯牛顿算法可能会有J’*J为奇异矩阵的情况,这时高斯牛顿法稳定性较差,可能导致算法不收敛。 1.1.1雅可比矩阵 Jacobian matrix雅可比矩阵是多元函数一阶偏导数以一定方式排列成的矩阵,体现了一个可微方程与给出点的最优线性逼近。以二元函数为例, 目标函数可以简写: S = ∑ i = 0 m r i 2 S=\sum_{i=0}^{m}r_i^2 S=∑i=0mri2 梯度向量在方向上的分量: g j = 2 ∑ i = 0 m r i 2 ∂ r i ∂ β j ( 1 ) g_j=2\sum_{i=0}^{m}r_i^2 \frac{∂_{r_i}}{∂_{β_j}}(1) gj=2∑i=0mri2∂βj∂ri(1) Hessian 矩阵的元素则直接在梯度向量的基础上求导: 将(1)(2)改写成 矩阵相乘形式: 参考:https://blog.csdn.net/jinshengtao/article/details/51615162 根据重投影误差求相机位姿(R,T为方程系数),常常将求解模型转化为非线性最小二乘问题。高斯牛顿法正是用于解决非线性最小二乘问题,达到数据拟合、参数估计和函数估计的目的。 假设我们研究如下形式的非线性最小二乘问题: 如果有大量观测点(多维),我们可以通过选择合理的T使得残差的平方和最小求得两个相机之间的位姿。机器视觉这块暂时不扩展,接着说怎么求非线性最小二乘问题。 若用牛顿法求式3,则牛顿迭代公式为: 那回过头来,高斯牛顿法里为啥要舍弃黑森矩阵的二阶偏导数呢?主要问题是因为牛顿法中Hessian矩阵中的二阶信息项通常难以计算或者花费的工作量很大,而利用整个H的割线近似也不可取,因为在计算梯度时已经得到J(x),这样H中的一阶信息项 J T J J^TJ JTJ几乎是现成的。 鉴于此,为了简化计算,获得有效算法,我们可用一阶导数信息逼近二阶信息项。 1.4 保证算法收敛的机制相机位置估计问题中适用GN方法的前提是,残差r接近于零或者接近线性函数从而,二阶信息项才可以忽略。通常称为“小残量问题”,否则高斯牛顿法不收敛。
优点: 对于零残量问题,即r=0,有局部二阶收敛速度 对于小残量问题,即r较小或接近线性,有快的局部收敛速度 对于线性最小二乘问题,一步达到极小点 缺点: 对于不是很严重的大残量问题,有较慢的局部收敛速度 对于残量很大的问题或r的非线性程度很大的问题,不收敛 不一定总体收敛 如果J不满秩,则方法无定义 1.5阻尼高斯牛顿法对于它的缺点,我们通过增加线性搜索策略,保证目标函数每一步下降,对于几乎所有非线性最小二乘问题,它都具有局部收敛性及总体收敛,即所谓的阻尼高斯牛顿法。
【reference】: [1]http://fourier.eng.hmc.edu/e176/lectures/NM/node36.html 【理论推导很完善】 [2].http://blog.csdn.net/dsbatigol/article/details/12448627 有关梯度下降法: http://www.cnblogs.com/shixiangwan/p/7532858.html https://www.zhihu.com/question/19723347 http://www.cnblogs.com/maybe2030/p/5089753.html 梯度下降与牛顿法: https://www.cnblogs.com/shixiangwan/p/7532830.html matlab练习程序(高斯牛顿法最优化)https://www.cnblogs.com/tiandsp/p/10213910.html 计算步骤如下: 代码如下: clear all; close all; clc; a=1;b=2;c=1; %待求解的系数 x=(0:0.01:1)'; w=rand(length(x),1)*2-1; %生成噪声 y=exp(a*x.^2+b*x+c)+w; %带噪声的模型 plot(x,y,'.') pre=rand(3,1); %步骤1 for i=1:1000 f = exp(pre(1)*x.^2+pre(2)*x+pre(3)); g = y-f; %步骤2中的误差 p1 = exp(pre(1)*x.^2+pre(2)*x+pre(3)).*x.^2; %对a求偏导 p2 = exp(pre(1)*x.^2+pre(2)*x+pre(3)).*x; %对b求偏导 p3 = exp(pre(1)*x.^2+pre(2)*x+pre(3)); %对c求偏导 J = [p1 p2 p3]; %步骤2中的雅克比矩阵 delta = inv(J'*J)*J'* g; %步骤3,inv(J'*J)*J'为H的逆 pcur = pre+delta; %步骤4 if norm(delta) |
【本文地址】
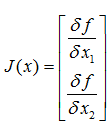 如果扩展多维的话F: Rn-> Rm,则雅可比矩阵是一个m行n列的矩阵:
如果扩展多维的话F: Rn-> Rm,则雅可比矩阵是一个m行n列的矩阵: 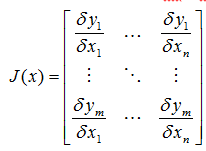 雅可比矩阵作用,如果
P
P
P是
R
n
R_n
Rn中的一点,
F
F
F在
P
P
P点可微分,那么在这一点的导数由
J
F
(
P
)
J_F(P)
JF(P)给出,在此情况下,由
F
(
P
)
F(P)
F(P)描述的线性算子即接近点
P
P
P的
F
F
F的最优线性逼近:
雅可比矩阵作用,如果
P
P
P是
R
n
R_n
Rn中的一点,
F
F
F在
P
P
P点可微分,那么在这一点的导数由
J
F
(
P
)
J_F(P)
JF(P)给出,在此情况下,由
F
(
P
)
F(P)
F(P)描述的线性算子即接近点
P
P
P的
F
F
F的最优线性逼近: 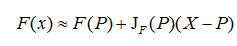
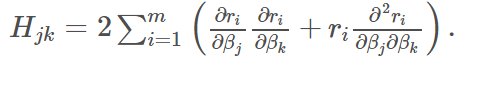 高斯牛顿法的一个小技巧是,将二次偏导省略,于是:
高斯牛顿法的一个小技巧是,将二次偏导省略,于是: 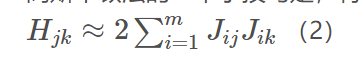

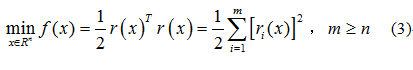

 这两个位置间残差(重投影误差):
这两个位置间残差(重投影误差): 
 看到这里大家都明白高斯牛顿和牛顿法的差异了吧,就在这迭代项上。经典高斯牛顿算法迭代步长λ为1.
看到这里大家都明白高斯牛顿和牛顿法的差异了吧,就在这迭代项上。经典高斯牛顿算法迭代步长λ为1.
 其中,
a
k
a^k
ak为一维搜索因子.
其中,
a
k
a^k
ak为一维搜索因子.
 下面使用书中的练习y=exp(ax^2+bx+c)+w这个模型验证一下,其中w为噪声,a、b、c为待解算系数。
下面使用书中的练习y=exp(ax^2+bx+c)+w这个模型验证一下,其中w为噪声,a、b、c为待解算系数。