叉乘、向量积的计算以及推导

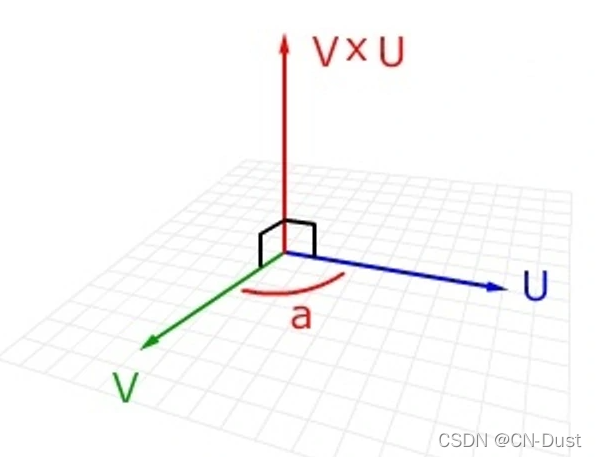
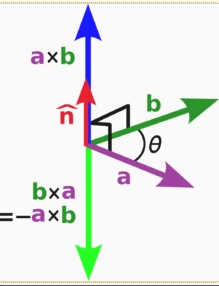
几何图示：

设有

a = ( a x , a y , a z ) , b = ( b x , b y , b z ) \mathbf{a}=\left(a_{x}, a_{y}, a_{z}\right), \mathbf{b}=\left(b_{x}, b_{y}, b_{z}\right) a=(ax​,ay​,az​),b=(bx​,by​,bz​)

i，j，k分别是X，Y，Z轴方向的单位向量，则：

a × b = ( a y b z − a z b y ) i + ( a z b x − a x b z ) j + ( a x b y − a y b x ) k \mathbf{a} \times \mathbf{b}=\left(a_{y} b_{z}-a_{z} b_{y}\right) \mathbf{i}+\left(a_{z} b_{x}-a_{x} b_{z}\right) \mathbf{j}+\left(a_{x} b_{y}-a_{y} b_{x}\right) \mathbf{k} a×b=(ay​bz​−az​by​)i+(az​bx​−ax​bz​)j+(ax​by​−ay​bx​)k

为了帮助记忆，利用三阶行列式，写成

∣ i j k a x a y a z b x b y b z ∣ \left|\begin{array}{lll} i & j & k \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{array}\right| ∣∣∣∣∣∣​iax​bx​​jay​by​​kaz​bz​​∣∣∣∣∣∣​

设a=(l,m,n),b=(o,p,q)，则

a × b = ( l , m , n ) × ( o , p , q ) = ( m q − n p , n o − l q , l p − m o ) \mathbf{a} \times \mathbf{b}=(l, m, n) \times(o, p, q)=(m q-n p, n o-l q, l p-m o) a×b=(l,m,n)×(o,p,q)=(mq−np,no−lq,lp−mo)

利用三阶行列式，写成

∣ i j k l m n o p q ∣ \left|\begin{array}{ccc} i & j & k \\ l & m & n \\ o & p & q \end{array}\right| ∣∣∣∣∣∣​ilo​jmp​knq​∣∣∣∣∣∣​

设有三个单位向量i，j，k，则： i → = ( 1 , 0 , 0 ) j → = ( 0 , 1 , 0 ) k → = ( 0 , 0 , 1 ) \begin{aligned} &\overrightarrow{\mathrm{i}}=(1,0,0) \\ &\overrightarrow{\mathrm{j}}=(0,1,0) \\ &\overrightarrow{\mathrm{k}}=(0,0,1) \end{aligned} ​i =(1,0,0)j ​=(0,1,0)k =(0,0,1)​

且 i → = j → × k → j → = k → × i → k → = i → × j → k → × j → = − i → i → × k → = − j → j → × i → = − k → i → × i → = j → × j → = k → × k → = 0 → = 0 \overrightarrow{\mathrm{i}}=\overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{k}}\\ \overrightarrow{\mathrm{j}}=\overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{i}}\\ \overrightarrow{\mathrm{k}}=\overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{j}}\\ \overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{j}}=- \overrightarrow{\mathrm{i}}\\ \overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{k}}=- \overrightarrow{\mathrm{j}}\\ \overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{i}}=- \overrightarrow{\mathrm{k}}\\ \overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{i}} = \overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{j}} = \overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{k}} = \overrightarrow{\mathrm{0}} = 0 i =j ​×k j ​=k ×i k =i ×j ​k ×j ​=−i i ×k =−j ​j ​×i =−k i ×i =j ​×j ​=k ×k =0 =0

i，j，k是三个相互垂直的向量。它们刚好可以构成一个坐标系。 对于处于i，j，k构成的坐标系中的向量u，v我们可以如下表示： u → = ( x u , y u , z u ) v → = ( x v , y v , z v ) \begin{aligned} &\overrightarrow{\mathrm{u}}=\left(\mathrm{x}_{\mathrm{u}}, \mathrm{y}_{\mathrm{u}}, \mathrm{z}_{\mathrm{u}}\right) \\ &\overrightarrow{\mathrm{v}}=\left(\mathrm{x}_{\mathrm{v}}, \mathrm{y}_{\mathrm{v}}, \mathrm{z}_{\mathrm{v}}\right) \end{aligned} ​u =(xu​,yu​,zu​)v =(xv​,yv​,zv​)​

u → = X u ⋅ i → + y u ⋅ j → + z u ⋅ k → v → = X v ⋅ i → + y v ⋅ j → + z v ⋅ k → \begin{aligned} &\overrightarrow{\mathrm{u}}=\mathrm{X}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{k}} \\ &\overrightarrow{\mathrm{v}}=\mathrm{X}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{k}} \end{aligned} ​u =Xu​⋅i +yu​⋅j ​+zu​⋅k v =Xv​⋅i +yv​⋅j ​+zv​⋅k ​

u → × v → = ( x u ⋅ i → + y u ⋅ j → + z u ⋅ k → ) × ( x v ⋅ i → + y v j → + z v ⋅ k → ) \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=\left(\mathrm{x}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{k}}\right) \times\left(\mathrm{x}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{v}} \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{k}}\right) u ×v =(xu​⋅i +yu​⋅j ​+zu​⋅k )×(xv​⋅i +yv​j ​+zv​⋅k )

展开，得：

u → × v → = x u ⋅ x v ⋅ ( i → ⋅ i → ) + x u ⋅ y v ⋅ ( i → ⋅ j → ) + x u ⋅ z v ⋅ ( i → ⋅ k → ) + y u ⋅ x v ⋅ ( j → ⋅ i → ) + y u ⋅ y v ⋅ ( j → ⋅ j → ) + y u ⋅ z v ⋅ ( j → ⋅ k → ) + z u ⋅ x v ⋅ ( k → ⋅ i → ) + z u ⋅ y v ⋅ ( k → ⋅ j → ) + z u ⋅ z v ⋅ ( k → ⋅ k → ) \begin{aligned} \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=& \mathrm{x}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{x}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{x}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{k}}) \\ &+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{k}}) \\ &+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{k}}) \end{aligned} u ×v =​xu​⋅xv​⋅(i ⋅i )+xu​⋅yv​⋅(i ⋅j ​)+xu​⋅zv​⋅(i ⋅k )+yu​⋅xv​⋅(j ​⋅i )+yu​⋅yv​⋅(j ​⋅j ​)+yu​⋅zv​⋅(j ​⋅k )+zu​⋅xv​⋅(k ⋅i )+zu​⋅yv​⋅(k ⋅j ​)+zu​⋅zv​⋅(k ⋅k )​

化简，得：

u ⃗ × v ⃗ = 0 → + x u ⋅ y v ⋅ ( k ⃗ ) + x u ⋅ z v ⋅ ( − j ⃗ ) + y u ⋅ x v ⋅ ( − k ⃗ ) + 0 → + y u ⋅ z v ⋅ ( i ⃗ ) + z u ⋅ x V ⋅ ( j ⃗ ) + z u ⋅ y v ⋅ ( − i ⃗ ) + 0 → \begin{gathered} \vec{u} \times \vec{v}=\overrightarrow{0}+x_{u} \cdot y_{v} \cdot(\vec{k})+x_{u} \cdot z_{v} \cdot(-\vec{j}) \\ +y_{u} \cdot x_{v} \cdot(-\vec{k})+\overrightarrow{0}+y_{u} \cdot z_{v} \cdot(\vec{i}) \\ +z_{u} \cdot x_{V} \cdot(\vec{j})+z_{u} \cdot y_{v} \cdot(-\vec{i})+\overrightarrow{0} \end{gathered} u ×v =0 +xu​⋅yv​⋅(k )+xu​⋅zv​⋅(−j ​)+yu​⋅xv​⋅(−k )+0 +yu​⋅zv​⋅(i )+zu​⋅xV​⋅(j ​)+zu​⋅yv​⋅(−i )+0 ​

合并，得：

u → × v → = ( y u ⋅ z v − z u ⋅ y v ) ⋅ ( i → ) + ( z u ⋅ x v − x u ⋅ z v ) ⋅ ( j → ) + ( x u ⋅ y v − y u ⋅ x v ) ⋅ ( k → ) \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=\left(\mathrm{y}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}}-\mathrm{z}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{i}})+\left(\mathrm{z}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}}-\mathrm{x}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{j}})+\left(\mathrm{x}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}}-\mathrm{y}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{k}}) u ×v =(yu​⋅zv​−zu​⋅yv​)⋅(i )+(zu​⋅xv​−xu​⋅zv​)⋅(j ​)+(xu​⋅yv​−yu​⋅xv​)⋅(k )

设 c → = a → × b → \overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}} c =a ×b

则c的方向垂直于a与b所决定的平面，c的指向按右手定则从a转向b来确定。 且c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。 ∣ c ∣ = ∣ a ∣ ∣ b ∣ ⋅ sin ⁡ θ |c|=|a||b|·\sin \theta ∣c∣=∣a∣∣b∣⋅sinθ

右手定则： 若坐标系是满足右手定则的，当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。

反交换律 a → × b → = − b → × a → \overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}=-\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{a}} a ×b =−b ×a

加法的分配律

a ⃗ × ( b ⃗ + c ⃗ ) = a ⃗ × b ⃗ + a ⃗ × c ⃗ \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} a ×(b +c )=a ×b +a ×c

与标量乘法兼容 r a → × b → = a → × r b → = r × ( a → × b → ) r\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{a}} \times r\overrightarrow{\mathrm{b}}=r \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) ra ×b =a ×rb =r×(a ×b )

不满足结合律，但满足雅可比恒等式 a → × ( b → × c → ) + b → × ( c → × a → ) + c → × ( a → × b → ) = 0 \overrightarrow{\mathrm{a}} \times(\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}})+\overrightarrow{\mathrm{b}} \times(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}})+\overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) = 0 a ×(b ×c )+b ×(c ×a )+c ×(a ×b )=0

分配律，线性性和雅可比恒等式别表明：具有向量加法和叉积的R3构成了一个李代数。

两个非零向量a和b平行，当且仅当a×b=0。

设向量坐标 a ⃗ = ( x 1 , y 1 , z 1 ) , b ⃗ = ( x 2 , y 2 , z 2 ) , c ⃗ = ( x 3 , y 3 , z 3 ) \vec{a}=(x 1, y 1, z 1), \vec{b}=(x 2, y 2, z 2), \vec{c}=(x 3, y 3, z 3) a =(x1,y1,z1),b =(x2,y2,z2),c =(x3,y3,z3), 则 ( a ⃗ × b ⃗ ) × c ⃗ = ( y 1 z 2 − z 1 y 2 , z 1 x 2 − x 1 z 2 , x 1 y 2 − x 2 y 1 ) × ( x 3 , y 3 , z 3 ) = ( z 1 z 3 x 2 − x 1 z 2 z 3 − x 1 y 2 y 3 + x 2 y 1 y 3 , x 1 x 3 y 2 − x 2 x 3 y 1 − y 1 z 2 z 3 + z 1 z 3 y 2 , y 1 y 3 z 2 − y 2 y 3 z 1 − x 2 x 3 z 1 + x 1 x 3 z 2 ) = ( x 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) , y 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) , z 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) ) − ( x 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) , y 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) , z 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) ) = ( x 2 ( a ⃗ ⋅ c ⃗ ) , y 2 ( a ⃗ ⋅ c ⃗ ) , z 2 ( a ⃗ ⋅ c ⃗ ) ) − ( x 1 ( b ⃗ ⋅ c ⃗ ) , y 1 ( b ⃗ ⋅ c ⃗ ) , z 1 ( b ⃗ ⋅ c ⃗ ) ) = b ⃗ ( a ⃗ ⋅ c ⃗ ) − a ⃗ ( b ⃗ ⋅ c ⃗ ) \begin{aligned} &(\vec{a} \times \vec{b}) \times \vec{c}=\left(y_{1} z_{2}-z_{1} y_{2}, z_{1} x_{2}-x_{1} z_{2}, x_{1} y_{2}-x_{2} y_{1}\right) \times\left(x_{3}, y_{3}, z_{3}\right) \\ &=\left(z_{1} z_{3} x_{2}-x_{1} z_{2} z_{3}-x_{1} y_{2} y_{3}+x_{2} y_{1} y_{3}, x_{1} x_{3} y_{2}-x_{2} x_{3} y_{1}\right. \\ &\left.-y_{1} z_{2} z_{3}+z_{1} z_{3} y_{2}, y_{1} y_{3} z_{2}-y_{2} y_{3} z_{1}-x_{2} x_{3} z_{1}+x_{1} x_{3} z_{2}\right) \\ &=\left(x_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right), y_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right), z_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right)\right) \\ &-\left(x_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right), y_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right), z_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right)\right) \\ &=\left(x_{2}(\vec{a} \cdot \vec{c}), y_{2}(\vec{a} \cdot \vec{c}), z_{2}(\vec{a} \cdot \vec{c})\right)-\left(x_{1}(\vec{b} \cdot \vec{c}), y_{1}(\vec{b} \cdot \vec{c}), z_{1}(\vec{b} \cdot \vec{c})\right) \\ &=\vec{b}(\vec{a} \cdot \vec{c})-\vec{a}(\vec{b} \cdot \vec{c}) \end{aligned} ​(a ×b )×c =(y1​z2​−z1​y2​,z1​x2​−x1​z2​,x1​y2​−x2​y1​)×(x3​,y3​,z3​)=(z1​z3​x2​−x1​z2​z3​−x1​y2​y3​+x2​y1​y3​,x1​x3​y2​−x2​x3​y1​−y1​z2​z3​+z1​z3​y2​,y1​y3​z2​−y2​y3​z1​−x2​x3​z1​+x1​x3​z2​)=(x2​(x1​x3​+y1​y3​+z1​z3​),y2​(x1​x3​+y1​y3​+z1​z3​),z2​(x1​x3​+y1​y3​+z1​z3​))−(x1​(x2​x3​+y2​y3​+z2​z3​),y1​(x2​x3​+y2​y3​+z2​z3​),z1​(x2​x3​+y2​y3​+z2​z3​))=(x2​(a ⋅c ),y2​(a ⋅c ),z2​(a ⋅c ))−(x1​(b ⋅c ),y1​(b ⋅c ),z1​(b ⋅c ))=b (a ⋅c )−a (b ⋅c )​ 这就是二重向量叉乘化简公式 ( a ⃗ × b ⃗ ) × c ⃗ = b ⃗ ( a ⃗ ⋅ c ⃗ ) − a ⃗ ( b ⃗ ⋅ c ⃗ ) (\vec{a} \times \vec{b}) \times \vec{c}=\vec{b}(\vec{a} \cdot \vec{c})-\vec{a}(\vec{b} \cdot \vec{c}) (a ×b )×c =b (a ⋅c )−a (b ⋅c )

转化一下，得 a ⃗ × ( b ⃗ × c ⃗ ) = b ⃗ ( a ⃗ ⋅ c ⃗ ) − c ⃗ ( a ⃗ ⋅ b ⃗ ) \vec{a} \times (\vec{b} \times \vec{c})=\vec{b}(\vec{a} \cdot \vec{c})-\vec{c}(\vec{a} \cdot \vec{b}) a ×(b ×c )=b (a ⋅c )−c (a ⋅b )