| 数学建模 | 您所在的位置:网站首页 › 泄水流量的观测方法有哪些 › 数学建模 |
数学建模
|
上篇博客中介绍了插值,插值的一些算法以及Matalb中的一些插值工具函数,这篇博文主要介绍拟合方法以及Matlab中的拟合函数和交互式页面。 一、 拟合方法 线性最小二乘法引入 (1) 概述:与插值相似,在工程中我们常常需要根据两个变量的几组实验数据来找出这两个变量之间的函数关系的近似表达式。我们将找到的近似表达式成为经验公式。但拟合与插值不同的是得到的经验公式不要求经过每一个数据点,而是要求点之间的总偏差最小。 (2) 引例: 为了测定刀具的磨损速度,我们做这样的实验:经过一定的时间(如每隔一小时),测量一次刀具的厚度,得到一组实验数据如下: 试根据上面的数据建立y与t之间的经验公式: 试根据上面的数据建立y与t之间的经验公式: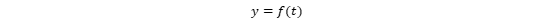 解:首先我们利用Matlab绘制已知数据点的散点图,观察数据的整体走向,以确定用何种类型的函数进行拟合: 解:首先我们利用Matlab绘制已知数据点的散点图,观察数据的整体走向,以确定用何种类型的函数进行拟合:  从上图可以看出,这些点的连线近似于一条直线,即线性函数,我们设: 从上图可以看出,这些点的连线近似于一条直线,即线性函数,我们设:  其中a和b时待定的系数。 我们接下来要做的就是确定a和b使f(t)=at+b在 其中a和b时待定的系数。 我们接下来要做的就是确定a和b使f(t)=at+b在 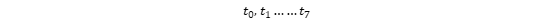 处的函数值与实验数据𝑦0,𝑦1……𝑦7相差都很少,就是要使偏差 处的函数值与实验数据𝑦0,𝑦1……𝑦7相差都很少,就是要使偏差 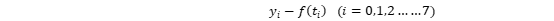 都很小。即 都很小。即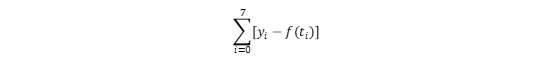 -----------------------------------------------① 最小。 由于偏差存在正负,要使整体偏差最小的话我们不能使偏差正负抵消的情况出现。为此我们可以对偏差取绝对值之后再相加。由于绝对值在实际处理中会对求导等增加复杂度,所以我们用平方法代替,即 -----------------------------------------------① 最小。 由于偏差存在正负,要使整体偏差最小的话我们不能使偏差正负抵消的情况出现。为此我们可以对偏差取绝对值之后再相加。由于绝对值在实际处理中会对求导等增加复杂度,所以我们用平方法代替,即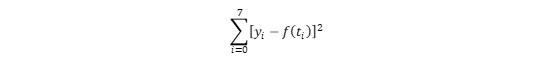 记做②式。由于f(t)=at+b,代入②得 记做②式。由于f(t)=at+b,代入②得 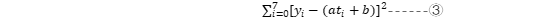 我们要求③的最小值,令 我们要求③的最小值,令  把M看做自 变量a和b对应的因变量,那么问题归结为求函数M=M(a , b)在哪些点取得最小值。即求方程组 把M看做自 变量a和b对应的因变量,那么问题归结为求函数M=M(a , b)在哪些点取得最小值。即求方程组  的解。即令 的解。即令 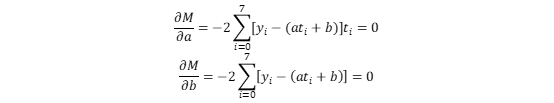 整理并合并同类项: 整理并合并同类项: 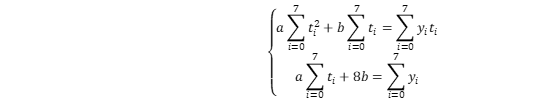 下面通过列表来计算 下面通过列表来计算
b. 拟合效果的判断: 先在直观判断的基础上,选择几种曲线进行拟合,然后比较,看哪一条曲线的最小二乘法指标J最小 最小二乘法的Matlab实现 (1) 解方程组的方法: 在上述的记号下: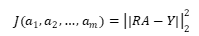 Matlab中的线性最小二乘法的标准型为 Matlab中的线性最小二乘法的标准型为 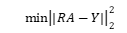 命令为A=R\Y 仍以上述的“刀具磨损速度”为例,使用Matlab中上述命令解题 命令为A=R\Y 仍以上述的“刀具磨损速度”为例,使用Matlab中上述命令解题  编写函数:
1. function f=matching3(X,Y)
2. syms x
3. n=length(X);
4. X=X';
5. Y=Y';
6. R=[ones(n,1),X.^1];
7. A=R\Y;
8. f=A(1)+A(2)*x;
9. plot(X,Y,'*b');
10. hold on
11. ezplot(f,[X(1),X(n)]);
12. title('A=R\\Y命令实现线性最小二乘');
13. legend('数据点','线性拟合曲线');
命令行窗口输入:
1. x0=[0:1:7];
2. y0=[27,26.8,26.5,26.3,26.1,25.7,25.3,24.8];
3. f=matching3(x0,y0) 编写函数:
1. function f=matching3(X,Y)
2. syms x
3. n=length(X);
4. X=X';
5. Y=Y';
6. R=[ones(n,1),X.^1];
7. A=R\Y;
8. f=A(1)+A(2)*x;
9. plot(X,Y,'*b');
10. hold on
11. ezplot(f,[X(1),X(n)]);
12. title('A=R\\Y命令实现线性最小二乘');
13. legend('数据点','线性拟合曲线');
命令行窗口输入:
1. x0=[0:1:7];
2. y0=[27,26.8,26.5,26.3,26.1,25.7,25.3,24.8];
3. f=matching3(x0,y0)
输出结果: 1. f = 2. 3. 217/8 - (17*x)/56绘制出图像: 命令行窗口输入以及输出结果: 1. >> [y11,y12]=matching2 2. 3. y11 = 4. 5. 233.4286 6. 7. 8. y12 = 9. 10. 253.9286(3) 最小二乘优化 无约束规划中,若目标函数可以由若干函数的平方和构成,一般这类函数可以写成 最小二乘优化是一类比较特殊的优化问题。在Matlab优化工具箱中提供了一系列函数—— ① lsqlin函数 有约束的线性最小二乘的标准形式是: 求解 求解结果: 1. f=matching4(x0,y0) 2. 3. f = 4. 5. 217/8 - (17*x)/56与前面使用A=R\Y命令效果一致。 ② lsqcurvefit函数 该函数为非线性拟合函数。在已知拟合数据向量xdata和ydata,并且知道xdata和ydata之间的函数关系ydata=F(x,xdata),仅仅不知道函数的某些系数系数向量x,可以用lsqcurvefit函数进行对未知系数的拟合,求x使下面的式子成立: 命令行窗口输入: 1. y0=matchingData(:,2); 2. x0=matchingData(:,[3:5]); 3. parameter0=rand(2,1);%拟合参数的初始值是任意取的 4. %非线性拟合的答案是不唯一的,下面给出拟合参数的上下限 5. lb=[2,1]; 6. ub=[20;2]; 7. %上下限不唯一,可以自己设定,不设定时默认值是空矩阵 8. parameter=lsqcurvefit(@matchingf,parameter0,x0,y0,lb,ub)输出结果(不唯一) 1. Initial point is a local minimum. 2. 3. Optimization completed because the size of the gradient at the initial point 4. is less than the value of the optimality tolerance. 5. 6. 7. 8. parameter = 9. 10. 11.0000 11. 1.5000例2: 用最小二乘法拟合 解:Matlab程序如下: 1. >> load('data3.mat') 2. >> mf=@(parameter,xdata)1/sqrt(2*pi)/parameter(2)*exp(-(xdata-parameter(1)).^2/2); 3. >> parameter=lsqcurvefit(mf,rand(2,1),x0,y0)输出结果: 1. Local minimum found. 2. 3. Optimization completed because the size of the gradient is less than 4. the value of the optimality tolerance. 5. 6. 7. 8. parameter = 9. 10. 0.0000 11. 1.0000③ lsqnonlin函数 非线性最小二乘(非线性拟合)的标准形式是: 输出结果: 1. Local minimum found. 2. 3. Optimization completed because the size of the gradient is less than 4. the value of the optimality tolerance. 5. 6. 7. 8. parameter = 9. 10. 0.0000 11. 1.0000④ lsqnonneg函数 非负线性最小二乘的标准形式是 运行结果: - >> run2 - - x = - - 0 - 0.6929⑤ Matlab的曲线拟合用户图形界面解法 Matlab提供了命令cftool,该命令给出了一维数据拟合的交互式环境。具体执行步骤如下: 把数据导入到工作空间运行cftool,打开用户图形界面窗口选择适当的模型进行拟合生成一些相关的统计量进行预测具体用法参见:CSDN某位daolao的博客 二、曲线拟合与函数逼近
概念引入 上述的曲线拟合是已知一组离散数据{(x_i,y_i ),i=1,…,n}选择一个较为简单的函数f(x),在一定的准则,如(最小二乘准则)下,最接近这组数据。 如果已知的是一个较为复杂的函数y=f(x),x∈[a,b],要求选择一个较为简单的函数f(x),在一定准则下最接近f(x),就是函数逼近。最小平方逼近 最小平方逼近的标准形式
二、曲线拟合与函数逼近
概念引入 上述的曲线拟合是已知一组离散数据{(x_i,y_i ),i=1,…,n}选择一个较为简单的函数f(x),在一定的准则,如(最小二乘准则)下,最接近这组数据。 如果已知的是一个较为复杂的函数y=f(x),x∈[a,b],要求选择一个较为简单的函数f(x),在一定准则下最接近f(x),就是函数逼近。最小平方逼近 最小平方逼近的标准形式 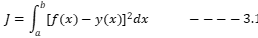 达到最小。与曲线拟合一样,选择一组函数{r_k (x),k=1,…,m}构造f(x),即令 达到最小。与曲线拟合一样,选择一组函数{r_k (x),k=1,…,m}构造f(x),即令  代入式子3.1,求a_1,…,a_m使J达到最小。利用极值必要条件可得: 代入式子3.1,求a_1,…,a_m使J达到最小。利用极值必要条件可得: 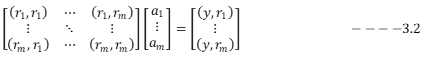 这里 这里 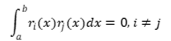 方程组3.2的系数矩阵为非奇异时,有唯一解。
四、 例题 方程组3.2的系数矩阵为非奇异时,有唯一解。
四、 例题
1.1 黄河小浪底调水调沙问题 问题的提出: 2004年6月至7月黄河进行了第三次调水调沙实验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙实验获得成功,整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日结束并恢复正常供水。小浪底水利工程按设计拦沙量为75.5亿m3,在这之前,小浪底共积泥沙达14.15亿t.这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙,在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于6月29日先后到达小浪底,7月3日达到最大流量2700m3/s,使小浪底水库的排沙量也不断增加。表1是由小浪底观测站从6月29日到7月10日检测到的试验数据。 其中i表示次数,计时单位:秒/s 根据题意得出等式:某一时刻排沙量=水流量×含沙量 记第i,(i=1,2,…,24)次观测时的排沙量为y_i,水流量为v_i,含沙量为c_i 则第i次观测时的排沙量为: y_i=v_i×c_i 由微分和积分的关系可知,任意时刻的总的排沙量等于各时刻的排沙量之和,记总的排沙量为z,则有: 命令行窗口输入命令以及输出结果: 1. >>[f,total]=Mymatching(HuangHe) 2. 3. f = 4. 5. 23×1 cell 数组 6. 7. {'1.446373*x - 0.000003145275*x^2 - 2.648125e-12*x^3 + 57600.0' } 8. {'1.159796*x - 0.000003488472*x^2 - 1.151619e-12*x^3 + 114000.0' } 9. {'0.8519441*x - 0.000003637722*x^2 - 6.389389e-12*x^3 + 157500.0' } 10. {'0.5018725*x - 0.000004465786*x^2 + 8.252551e-11*x^3 + 187000.0' } 11. {'0.5780658*x + 0.000006229519*x^2 - 1.041684e-10*x^3 + 207000.0' } 12. {'0.5330865*x - 0.000007270706*x^2 + 6.622972e-11*x^3 + 235200.0' } 13. {'0.2756992*x + 0.000001312666*x^2 + 1.041959e-11*x^3 + 250000.0' } 14. {'0.4474499*x + 0.000002663045*x^2 - 4.09285e-11*x^3 + 265200.0' } 15. {'0.4483899*x - 0.000002641288*x^2 + 2.181593e-11*x^3 + 286200.0' } 16. {'0.3423239*x + 0.0000001860564*x^2 - 5.873884e-11*x^3 + 302400.0' } 17. {'0.02953683*x - 0.000007426497*x^2 + 8.910315e-11*x^3 + 312800.0' } 18. {'0.000004121271*x^2 - 0.113249*x - 4.215901e-11*x^3 + 307400.0' } 19. {'0.006792364*x - 0.000001342536*x^2 - 5.690704e-11*x^3 + 306800.0'} 20. {'7.629057e-11*x^3 - 0.000008717689*x^2 - 0.4278094*x + 300000.0' } 21. {'0.000001169569*x^2 - 0.7538882*x - 1.24219e-10*x^3 + 271400.0' } 22. {'1.87397e-10*x^3 - 0.00001492921*x^2 - 1.348305*x + 231000.0' } 23. {'0.000009357448*x^2 - 1.589005*x + 2.706168e-11*x^3 + 160000.0' } 24. {'0.00001286464*x^2 - 0.6290103*x - 2.088184e-10*x^3 + 111000.0' } 25. {'2.376449e-10*x^3 - 0.00001419822*x^2 - 0.6866208*x + 91000.0' } 26. {'0.00001660056*x^2 - 0.5828398*x - 1.773961e-10*x^3 + 54000.0' } 27. {'3.161053e-11*x^3 - 0.000006389971*x^2 - 0.1417424*x + 45500.0' } 28. {'5.715577e-11*x^3 - 0.000002293247*x^2 - 0.5168574*x + 30000.0' } 29. {'0.000005114141*x^2 - 0.3949948*x + 4.985713e-11*x^3 + 8000.0' } 30. 31. 32. total = 33. 34. 1.8440e+11
(2) 确定排沙量与水流量的关系。 由上拟合曲线图可知排沙量随着时间的变化大致分为两个阶段: 7月4日前排沙量不断增加,之后排沙量不断减少,而根据表格可以得到水流量在前一段时间随时间推进而增加,后一段时间随着时间推进而减少,所以我们大致可以将水流量与排沙量之间的关系分为两个阶段分别进行拟合。 我们对于两个阶段都分别采用一次拟合和二次拟合来进行,并且以标准差来作为最后选取的标准: 6月29日~7月4日y=250.5655v-373384 7月5日~7月10日y=0.1067v^2-180.4668v+72421.0982 实现Matlab代码如下: 1. function speedWithSand(data) 2. %准备两个阶段的数据 3. syms x 4. data1=data([1:12],:); 5. data2=data([13:23],:); 6. speed1=data1(:,1); 7. sand1=data1(:,2).*speed1; 8. speed2=data2(:,1); 9. sand2=data2(:,2).*speed2; 10. %进行第一分阶段的拟合 11. format long e 12. rmse1=ones(2,1); 13. rmse2=ones(2,1); 14. cha1=ones(2,1); 15. cha2=ones(2,1); 16. for j=1:2 17. match1{j}=polyfit(speed1,sand1,j); %拟合多项式 18. forcast1{j}=polyval(match1{j},speed1);%求出预测值 19. %以下求误差平方和以及剩余标准差 20. cha1(j)=sum((sand1-forcast1{j}).^2); 21. rmse1(j)=sqrt(cha1(j)/(10-j)); 22. end 23. celldisp(match1) 24. rmse1 25. 26. for j=1:2 27. match2{j}=polyfit(speed2,sand2,j); %拟合多项式 28. forcast2{j}=polyval(match2{j},speed2);%求出预测值 29. %以下求误差平方和以及剩余标准差 30. cha2(j)=sum((sand2-forcast2{j}).^2); 31. rmse2(j)=sqrt(cha2(j)/(10-j)); 32. end 33. celldisp(match1) 34. rmse2 35. format命令行窗口输入以及输出结果: 1. >> speedWithSand(HuangHe) 2. 3. match1{1} = 4. 5. 2.546957330612737e+02 -3.818018589089608e+05 6. 7. 8. 9. match1{2} = 10. 11. -4.973604894806963e-02 4.821949815832189e+02 -6.369512800128722e+05 12. 13. 14. 15. rmse1 = 16. 17. 1.135270235952025e+04 18. 1.111634607843465e+04 19. 20. 21. match1{1} = 22. 23. 2.546957330612737e+02 -3.818018589089608e+05 24. 25. 26. 27. match1{2} = 28. 29. -4.973604894806963e-02 4.821949815832189e+02 -6.369512800128722e+05 30. 31. 32. 33. rmse2 = 34. 35. 4.378235683047678e+04 36. 3.053573018955462e+04 |
【本文地址】
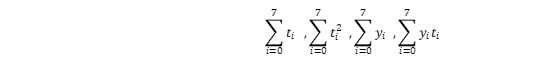
 代入方程组得:
代入方程组得: 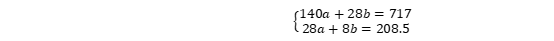 解此方程组得a=-0.3036,b=27.125. 这样,我们便得到所求的经验公式为 y=f(t)=-0.3036t+27.125 (3) 线性最小二乘法 线性最小二乘法是解决曲线拟合的最常用的方法,基本思路: 令
解此方程组得a=-0.3036,b=27.125. 这样,我们便得到所求的经验公式为 y=f(t)=-0.3036t+27.125 (3) 线性最小二乘法 线性最小二乘法是解决曲线拟合的最常用的方法,基本思路: 令 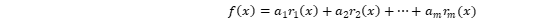 注:r_k (x)为事先选取的一组线性无关的函数 a_k为待定系数 系数a_k的确定 记
注:r_k (x)为事先选取的一组线性无关的函数 a_k为待定系数 系数a_k的确定 记 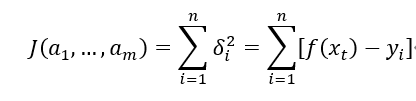 为了求a1,a2,…,am使J达到最小,只需要利用极值的必要条件
为了求a1,a2,…,am使J达到最小,只需要利用极值的必要条件 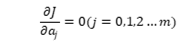 得到关于a1…am的线性方程组
得到关于a1…am的线性方程组 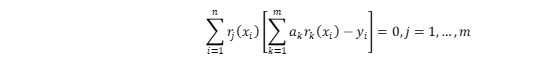 即
即 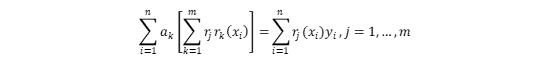 记
记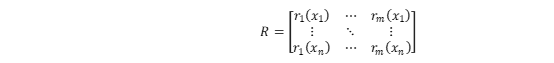 为n×m矩阵
为n×m矩阵 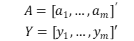 则③可表示为:
则③可表示为:  当
当 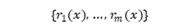 线性无关时,R列满秩,R^T R可逆,于是方程组④有唯一解:
线性无关时,R列满秩,R^T R可逆,于是方程组④有唯一解: 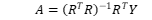 ii. 函数r_k (x)的选取 a. 先做散点图大致判断用什么曲线去拟合,常用的拟合曲线有: 直线:a_1 x+a_2 多项式:y=a_1 x^m+⋯+a_m x+a_(m+1)(一般m=2,3,不宜太高) 双曲线(一只):y=a_1/x+a_2 指数函数:y=a_1 e^(a_2 x) 特别的:对于指数函数,拟合前要做变量替换,转换成对a_1,a_2的线性函数。
ii. 函数r_k (x)的选取 a. 先做散点图大致判断用什么曲线去拟合,常用的拟合曲线有: 直线:a_1 x+a_2 多项式:y=a_1 x^m+⋯+a_m x+a_(m+1)(一般m=2,3,不宜太高) 双曲线(一只):y=a_1/x+a_2 指数函数:y=a_1 e^(a_2 x) 特别的:对于指数函数,拟合前要做变量替换,转换成对a_1,a_2的线性函数。 (2) 多项式拟合方法 如果选取多项式进行拟合
(2) 多项式拟合方法 如果选取多项式进行拟合 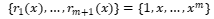 即用m次多项式拟合给定数据,Matlab中有现成的函数:
即用m次多项式拟合给定数据,Matlab中有现成的函数: 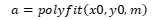 其中x0和y0为需要拟合的数据,m为拟合多项式的次数。 返回值a是拟合多项式
其中x0和y0为需要拟合的数据,m为拟合多项式的次数。 返回值a是拟合多项式 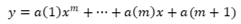 的系数向量
的系数向量 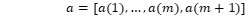 多项式在x处的值y可以用下面的函数计算:
多项式在x处的值y可以用下面的函数计算: 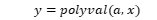 例: 某乡镇1990-1996年的生产利润如下表:
例: 某乡镇1990-1996年的生产利润如下表:  代码如下:
代码如下: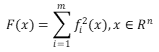 式中x=[x_1,…,x_n]’,一般假设m大于等于n。
式中x=[x_1,…,x_n]’,一般假设m大于等于n。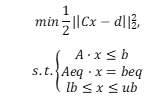 式中:C,A,Aeq为矩阵;d,b,beq,lb,ub,x为向量。 Matlab中的函数为: x=lsqlin(c,d,A,b,Aeq,beq,lb,ub,x0) 例:用该函数解例“刀具磨损速度”例题 代码:
式中:C,A,Aeq为矩阵;d,b,beq,lb,ub,x为向量。 Matlab中的函数为: x=lsqlin(c,d,A,b,Aeq,beq,lb,ub,x0) 例:用该函数解例“刀具磨损速度”例题 代码: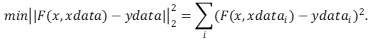 语法格式:
语法格式: 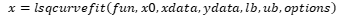 其中:fun为定义函数F(x,xdata)的M文件。 例:用下表给出的数据,拟合函数
其中:fun为定义函数F(x,xdata)的M文件。 例:用下表给出的数据,拟合函数 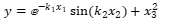 中的参数k1,k2
中的参数k1,k2  编写程序:
编写程序: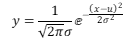 中的未知参数u,σ其中已知数据x_i,y_i (i=1,2,…,n)分别放在Matlab数据文件data3.mat中的x0,y0中,这里的data3.mat是由如下的Matlab产生的:
中的未知参数u,σ其中已知数据x_i,y_i (i=1,2,…,n)分别放在Matlab数据文件data3.mat中的x0,y0中,这里的data3.mat是由如下的Matlab产生的: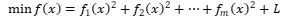 其中L为常数 在Matlab中使用lsqnonlin求解这类问题,语法如下:
其中L为常数 在Matlab中使用lsqnonlin求解这类问题,语法如下: 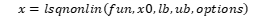 其中:fun是定义向量函数F(x)的M文件 例:用lsqnonlin求解上述例二
其中:fun是定义向量函数F(x)的M文件 例:用lsqnonlin求解上述例二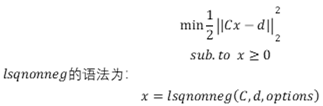

 现在,根据试验数据建立数学模型研究下面的问题: (1) 给出估计任意时刻的排沙量及总排沙量的方法; 解:从6月29日零时开始,观测的时刻分别为:
现在,根据试验数据建立数学模型研究下面的问题: (1) 给出估计任意时刻的排沙量及总排沙量的方法; 解:从6月29日零时开始,观测的时刻分别为: 求解程序如下:
求解程序如下: 得出总排沙量为1.844×10^11 t
得出总排沙量为1.844×10^11 t