| 信道编码基础(生成校验矩阵、码的个数、循环码) | 您所在的位置:网站首页 › 汉明码信道编码怎么看 › 信道编码基础(生成校验矩阵、码的个数、循环码) |
信道编码基础(生成校验矩阵、码的个数、循环码)
|
1. 有限域
1.1 有限域的characteristic。 对于一个有限域 F F F,记它的单位元为 e e e,则存在一个最小整数 p p p,使得 e + e + ⋯ + e ⏟ p 个 = 0 , \underbrace{e+e+\cdots+e}_{p \text{个}}=0, p个 e+e+⋯+e=0,则称 p p p是 F F F的characteristic。 ■ \blacksquare ■ 1.2 一个有限域的characteristic一定是质数(prime)。 ■ \blacksquare ■ 1.3 一个有限域的大小一定是characteristic的幂次(power),即 ∣ F ∣ = p a |F|=p^a ∣F∣=pa,其中 a a a是一个正整数。 ■ \blacksquare ■ 举例,一个有限域 G F ( 2 7 ) GF(2^7) GF(27)的characteristic是2,有限域元素个数为 2 7 2^7 27,是characteristic的幂次。 1.4 考虑一个有限域 F F F及其characteristic p p p,则对任意两个 F F F中的元素有 ( a + b ) p = a p + b p . (a+b)^p=a^p+b^p. (a+b)p=ap+bp. 证明: 先利用二项公式打开括号,得到 ( a + b ) p = ∑ i = 0 p C p i a i b p − i = a p + b p + ∑ i = 1 p − 1 C p i a i b p − i . (a+b)^p=\sum^{p}_{i=0}C^{i}_{p}a^ib^{p-i}=a^p+b^p+\sum^{p-1}_{i=1}C^{i}_{p}a^ib^{p-i}. (a+b)p=i=0∑pCpiaibp−i=ap+bp+i=1∑p−1Cpiaibp−i.当 1 ≤ i ≤ p − 1 1\leq i\leq p-1 1≤i≤p−1时, C p i = p ! ( p − i ) ! i ! . C^{i}_{p}=\frac{p!}{(p-i)!i!}. Cpi=(p−i)!i!p!.因为 p p p是一个质数,因此上式中分母部分没有因子 p p p,所以 C p i C^{i}_{p} Cpi必然是 p p p的倍数,这意味着 C p i a i b p − i = 0 C^{i}_{p}a^ib^{p-i}=0 Cpiaibp−i=0。综上,有 ( a + b ) p = a p + b p . (a+b)^p=a^p+b^p. (a+b)p=ap+bp. ■ \blacksquare ■ 1.5 利用1.4很容易得到 ( a 1 + a 2 + ⋯ + a n ) p k = a 1 p k + a 2 p k + ⋯ + a n p k . (a_1+a_2+\cdots+a_n)^{p^k}=a^{p^k}_1+a^{p^k}_2+\cdots+a^{p^k}_n. (a1+a2+⋯+an)pk=a1pk+a2pk+⋯+anpk.其中 a i ∈ F a_i\in F ai∈F, p p p是 F F F的characteristic, k k k是正整数。 ■ \blacksquare ■ 1.6 考虑将1.4推广至多项式形式。假设 a a a和 b b b是两个 F F F中的元素,并且 p p p是 F F F的characteristic,则 ( a x + b y ) p = a p x p + b p y p . (ax+by)^p=a^px^p+b^py^p. (ax+by)p=apxp+bpyp. 证明: 由1.4的证明可知 ( a x + b y ) p = a p x p + b p y p + ∑ i = 1 p − 1 C p i a i x i b p − i y p − i . (ax+by)^p=a^px^p+b^py^p+\sum^{p-1}_{i=1}C^{i}_{p}a^ix^ib^{p-i}y^{p-i}. (ax+by)p=apxp+bpyp+i=1∑p−1Cpiaixibp−iyp−i.因为 C p i C^{i}_{p} Cpi是 p p p的倍数,所以 C p i a i x i b p − i y p − i = 0. C^{i}_{p}a^ix^ib^{p-i}y^{p-i}=0. Cpiaixibp−iyp−i=0. ■ \blacksquare ■ 1.7 考虑一个多项式 f ( x ) = f 0 + f 1 x + f 2 x 2 + ⋯ + f n x n , f(x)=f_0+f_1x+f_2x^2+\cdots+f_nx^n, f(x)=f0+f1x+f2x2+⋯+fnxn,其中 f i ∈ F f_i\in F fi∈F.记 F F F的characteristic为 p p p,对于正整数 k k k,有 f p k ( x ) = f ( x p k ) . f^{p^k}(x)=f(x^{p^k}). fpk(x)=f(xpk). 因此对于一个有限域GF( p n p^n pn),有 f p n ( x ) = f ( x p n ) . f^{p^n}(x)=f(x^{p^n}). fpn(x)=f(xpn). ■ \blacksquare ■ 1.8 不可约多项式: 一个 F F F上的多项式如果不能被另一个次数小于自己且大于0的 F F F上的多项式整除,则称该多项式为不可约多项式(irreducible polynomial)。 ■ \blacksquare ■ 1.9 最小多项式: 考虑一个有限域GF( q q q)及其扩域GF( q m q^m qm),记 β \beta β是GF( q m q^m qm)中的一个元素。考虑等式 β q k = β , \beta^{q^k}=\beta, βqk=β,记 d d d为满足该等式的最小正整数。则 β \beta β在GF( q q q)上的最小多项式为 ∏ i = 1 d − 1 ( x − β q i ) . \prod^{d-1}_{i=1}(x-\beta^{q^i}). i=1∏d−1(x−βqi). ■ \blacksquare ■ 1.10 设 β \beta β是GF( q m q^m qm)上的元素, ϕ ( x ) \phi(x) ϕ(x)使其在GF( q q q)上的最小多项式,则: 显然 ϕ ( β ) = 0 \phi(\beta)=0 ϕ(β)=0可以证到 ϕ ( x ) \phi(x) ϕ(x)是拥有根 β \beta β的次数最小的GF( q q q)上的多项式(最小多项式名称的由来)。 ϕ ( x ) \phi(x) ϕ(x)是不可约的(如果可约则有更低次多项式有根 β \beta β)。 ■ \blacksquare ■ 2. 生成矩阵与校验矩阵2.1 生成矩阵和校验矩阵均是行满秩的。 ■ \blacksquare ■ 2.2 记一个线性码的最小距离为 d d d,则: 其校验矩阵 H H H存在 d d d列线性相关,每 d − 1 d-1 d−1列线性无关生成矩阵 G G G的每 n − d + 1 n-d+1 n−d+1列无关■ \blacksquare ■ 2.3 记一个MDS码的最小距离为 d d d,则: 其校验矩阵 H H H的每 n − k n-k n−k列线性无关生成矩阵 G G G的每 k k k列无关■ \blacksquare ■ 2.4 MDS码的对偶码也是MDS码。 ■ \blacksquare ■ 3. Syndrome decoding考虑一个基于有限域
F
F
F的
(
n
,
k
)
(n,k)
(n,k)线性码,将其码字全部列出,记为一个陪集(coset)。在向量空间
F
n
F^n
Fn中除去该线性码的向量中选择重量最小的,与线性码的码字相加,得到新的向量,组成一个新的陪集。继续在
F
n
F^n
Fn的还没使用的向量中找重量最小的向量,与线性码的码字相加,得到一组新的向量,即一个新的陪集。重复这样的操作知道整个向量空间的向量全部被找出。 4.1 二元汉明码的定义。 考虑大小为 m × ( 2 m − 1 ) m\times (2^m-1) m×(2m−1)的校验矩阵 H H H,他由 2 m − 1 2^m-1 2m−1个GF(2)上的非零列向量组成。该校验矩阵对应一个汉明码,最小距离为 d = 3 d=3 d=3。 ■ \blacksquare ■ 4.2 非二元汉明码的定义。 考虑有限域GF( q q q),和一个GF( q q q)上的大小为 m × q m − 1 q − 1 m\times \frac{q^m-1}{q-1} m×q−1qm−1的校验矩阵 H H H,他由 q m − 1 q − 1 \frac{q^m-1}{q-1} q−1qm−1个GF( q q q)上的非零列向量组成,并且任意两个列向量不为倍数关系。该校验矩阵对应一个非二元汉明码,最小距离为 d = 3 d=3 d=3。 对于GF( q q q)上的非零列向量,乘上一个非零元素可以得到一个新的列向量,把这些列向量看做一组。因此一个GF( q q q)上的长度为 m m m的列向量一共有 q m − 1 q − 1 \frac{q^m-1}{q-1} q−1qm−1组,非二元汉明码的校验矩阵的每一列对应一组。 ■ \blacksquare ■ 4.3 循环码的任意码字循环移位仍是该循环码的一个码字。 ■ \blacksquare ■ 4.4 一个 ( n , k ) (n,k) (n,k)循环码可以用一个次数为 n − k n-k n−k的生成多项式 g ( x ) g(x) g(x)表示。记消息多项式为 m ( x ) m(x) m(x),其次数为 k − 1 k-1 k−1,则 ( n , k ) (n,k) (n,k)循环码的码字多项式为 c ( x ) = m ( x ) g ( x ) . c(x)=m(x)g(x). c(x)=m(x)g(x). ■ \blacksquare ■ 4.5 如何得到一个循环码的生成多项式? 考虑有限域GF( q q q),则基于GF( q q q)的多项式 x n − 1 x^n-1 xn−1有若干因式,每一个因式就是一个循环码的生成多项式,即每一个因式对应一个循环码。 ■ \blacksquare ■ 4.6 一个生成多项式为
g
(
x
)
=
g
0
+
g
1
x
+
⋯
+
g
n
−
k
x
n
−
k
g(x)=g_0+g_1x+\cdots+g_{n-k}x^{n-k}
g(x)=g0+g1x+⋯+gn−kxn−k的生成多项式为 4.7 根据4.5可知一个循环码的生成多项式整除
x
n
−
1
x^n-1
xn−1,记
h
(
x
)
=
x
n
−
1
g
(
x
)
.
h(x)=\frac{x^n-1}{g(x)}.
h(x)=g(x)xn−1.则
h
(
x
)
h(x)
h(x)称为该循环码的校验多项式。记
h
(
x
)
=
h
0
+
h
1
x
+
⋯
+
h
k
x
k
,
h(x)=h_0+h_1x+\cdots+h_kx^k,
h(x)=h0+h1x+⋯+hkxk,则该循环码的校验矩阵为 4.8 一个生成多项式为 g ( x ) g(x) g(x)的循环码的校验多项式为 h ( x ) = x n − 1 g ( x ) h(x)=\frac{x^n-1}{g(x)} h(x)=g(x)xn−1,他的反多项式(reciprocal polynomial)记为 h ~ ( x ) = x k h ( x − k ) = h k + h k − 1 x + ⋯ + h 0 x k , \tilde{h}(x)=x^kh(x^{-k})=h_k+h_{k-1}x+\cdots+h_0x^k, h~(x)=xkh(x−k)=hk+hk−1x+⋯+h0xk,该反多项式是该循环码的对偶码的生成多项式,即该对偶码也是一个循环码,并且该对偶码的生成矩阵为4.7中的校验矩阵。 ■ \blacksquare ■ 5. 码的个数5.1 有限域 F q F_q Fq上的一个行满秩的大小为 m × n m\times n m×n的矩阵的个数为 ∏ i = 0 m − 1 ( q n − q i ) . \prod^{m-1}_{i=0}(q^n-q^i). i=0∏m−1(qn−qi).逐行构建,每一行不能是之前行的线性组合。 ■ \blacksquare ■ 5.2 给定一个 ( n , k ) (n,k) (n,k)线性码,其生成矩阵的个数为 ∏ i = 0 k − 1 ( q k − q i ) . \prod^{k-1}_{i=0}(q^k-q^i). i=0∏k−1(qk−qi).逐行构建,每一行不能是之前行的线性组合,并且行向量的总数为 2 k 2^k 2k。 ■ \blacksquare ■ 5.3 根据5.1 和5.2 ,有限域 F q F_q Fq上的 ( n , k ) (n,k) (n,k)的线性码的个数为 ∏ i = 0 m − 1 ( q n − q i ) ∏ i = 0 k − 1 ( q k − q i ) = ( q n − 1 ) ( q n − 1 − 1 ) ⋯ ( q n − k + 1 − 1 ) ( q k − 1 ) ( q k − 1 − 1 ) ⋯ ( q − 1 ) . \frac{\prod^{m-1}_{i=0}(q^n-q^i)}{\prod^{k-1}_{i=0}(q^k-q^i)}=\frac{(q^n-1)(q^{n-1}-1)\cdots(q^{n-k+1}-1)}{(q^k-1)(q^{k-1}-1)\cdots(q-1)}. ∏i=0k−1(qk−qi)∏i=0m−1(qn−qi)=(qk−1)(qk−1−1)⋯(q−1)(qn−1)(qn−1−1)⋯(qn−k+1−1). ■ \blacksquare ■ 5.4 二元汉明码的所有校验矩阵个数为 n ! . n!. n!.给定一个二元汉明码,其校验矩阵个数为 ∏ i = 0 m − 1 ( q m − q i ) . \prod^{m-1}_{i=0}(q^m-q^i). i=0∏m−1(qm−qi).因此二元汉明码的个数为 n ! ∏ i = 0 m − 1 ( q m − q i ) . \frac{n!}{\prod^{m-1}_{i=0}(q^m-q^i).} ∏i=0m−1(qm−qi).n! ■ \blacksquare ■ 5.5 非二元汉明码的所有校验矩阵个数为 ( q − 1 ) n n ! . (q-1)^nn!. (q−1)nn!.这里的 ( q − 1 ) n (q-1)^n (q−1)n是因为每一列都可以乘上一个非零的其他元素得到一个新的列。给定一个非二元汉明码,其校验矩阵个数为 ∏ i = 0 m − 1 ( q m − q i ) . \prod^{m-1}_{i=0}(q^m-q^i). i=0∏m−1(qm−qi).因此二元汉明码的个数为 ( q − 1 ) n n ! ∏ i = 0 m − 1 ( q m − q i ) . \frac{(q-1)^nn!}{\prod^{m-1}_{i=0}(q^m-q^i).} ∏i=0m−1(qm−qi).(q−1)nn! 需要注意非二元汉明码的码长为 n = q m − 1 q − 1 n=\frac{q^m-1}{q-1} n=q−1qm−1. ■ \blacksquare ■ 5.5 一个 F q F_q Fq上的循环码的个数与 F q F_q Fq上的多项式 x n − 1 x^n-1 xn−1的因式的个数相同。 ■ \blacksquare ■ 参考文献[1] Roman S . Coding and information theory,1992。 [2] 林舒,差错控制编码。 |
【本文地址】
 上图给了一个陪集的例子,第一行是一个线性码的所有码字,组成一个陪集。在组建第二行的陪集时,在第一行之外的向量中找到重量最小的向量00100,加到第一行上,得到新的陪集。重复操作得到所有向量。 syndrome decoding将先计算接收到的向量的校正子
s
=
y
H
T
.
s=\bm{y}H^T.
s=yHT.如果通过校正子找到对应的陪集,陪集首被认为就是错误向量。
■
\blacksquare
■
上图给了一个陪集的例子,第一行是一个线性码的所有码字,组成一个陪集。在组建第二行的陪集时,在第一行之外的向量中找到重量最小的向量00100,加到第一行上,得到新的陪集。重复操作得到所有向量。 syndrome decoding将先计算接收到的向量的校正子
s
=
y
H
T
.
s=\bm{y}H^T.
s=yHT.如果通过校正子找到对应的陪集,陪集首被认为就是错误向量。
■
\blacksquare
■ 他是生成多项式的系数向量移位得到的。
■
\blacksquare
■
他是生成多项式的系数向量移位得到的。
■
\blacksquare
■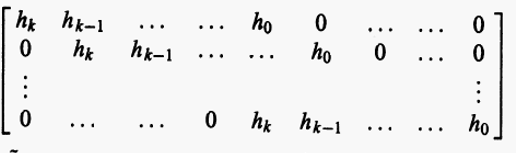 ■
\blacksquare
■
■
\blacksquare
■