导数，数值微分，偏导数，以及梯度下降的Python示例

2023-07-16 06:42| 来源: 网络整理| 查看: 265

目录导数数值微分偏导数梯度（gradient）

导数

一个函数在某一点的导数描述了这个函数在这一点附近的变化率：在这里插入图片描述例如一元函数中，某一点的p导数，描述了该点切线的斜率：

数值微分

解析性求导：利用数学推导计算导数，如： y=x2, 则y’=2x 数值微分：利用微小的差分求导。即根据导数定义公式，代入一个极小的∆x，求出变化率。

python示例：分别用数值微分和解析求导计算f=x2在x=2处的导数：

#定义函数f def f(x): return x*x # 定义数值微分计算方法 def numerical_diff(f, x): h = 1e-4 #0.0001，∆x,注意不能太小，会导致舍入误差而变成0 return (f(x+h)-f(x-h))/(2*h) #计算变化率 x=2 print('数值微分结果：{}'.format(numerical_diff(f, x))) print('解析求导结果:{}'.format(2*x)) 偏导数

对于有多个自变量的函数，例如Z=f(X,Y),有下图：在x保持不变的情况下（图中的黑线），Z值仅随Y值变化，该变化率即为函数对Y的偏导（图中斜率）在这里插入图片描述计算偏导时，将其他自变量视为常数。例：求y=x2+3xy+y2在点（1,2）处对x的偏导数解：将y视为常量，根据求导公式： y’=2x+3y, 所以在点(1,2)处对x的偏导数为：2×1+3×2=8

梯度（gradient）

对于有多个变量的函数，对每个变量分别计算偏导数，这些偏导数汇合而成的向量，称为梯度。对于上面举的例子，在某一点分别计算X和Y的偏导数，这两个偏导数组成的向量，就是梯度。梯度代表着函数值变化率最快的方向：在这里插入图片描述梯度计算的python示例：令：y=x02+x12

import numpy as np # 定义函数，主要x为二维数组 def f(x): return x[0]**2+x[1]**2 # 通过数值微分计算梯度，注意x为数组 def numerical_gradient(f,x): h=1e-4 #0.0001，∆x,注意不能太小，会导致舍入误差而变成0 grad=np.zeros_like(x) for index in range(x.size): #计算第index个x的偏导数 temp_val=x[index] x[index]=temp_val+h fxh1=f(x) x[index]=temp_val-h fxh2=f(x) # 将偏导数存为梯度向量 grad[index]=(fxh1-fxh2)/(2*h) x[index]=temp_val return grad # 随便计算两个点的梯度 print(numerical_gradient(f,np.array([3.0,4.0]))) print(numerical_gradient(f,np.array([0.0,2.0])))

输出结果为 [6. 8.] [0. 4.]

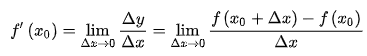#梯度的直观理解上例中，y=x02+x12,通过python画图如下：在这里插入图片描述我们将x0和x1在[-2,2]区间内每个点的‘负梯度’计算并用python画出来：可以看到，每个点的梯度都指向（0,0）点，这一点正是令函数值最小的点（函数值为0），而且距离该点越远，梯度越大，意味着函数值下降的速度越快。这个特性，在机器学习中具有非常重要的作用！

【本文地址】

公司简介

联系我们