| 反双曲三角函数 | 您所在的位置:网站首页 › 正弦函数的基本形式 › 反双曲三角函数 |
反双曲三角函数
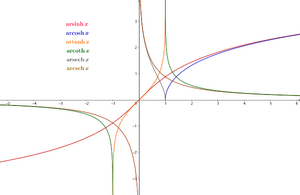 反双曲三角函数是作为双曲三角函数的反函数出现的。 目录 1 定义 2 双曲复合 3 微分 4 积分 5 级数展开 6 参见 定义[]反双曲函数可以用双曲函数来定义,例如将双曲正弦函数 y = sinh x {\displaystyle y=\operatorname {sinh} x} 给定一个确定的 y 0 ∈ R {\displaystyle y_{0}\in \mathbb {R} } ,方程 sinh x = y 0 {\displaystyle \operatorname {sinh} x=y_{0}} 的解 x = x 0 {\displaystyle x=x_{0}} 就称作 y 0 {\displaystyle y_{0}} 的反双曲正弦,记作 x 0 = arsinh y 0 . {\displaystyle x_{0}=\operatorname {arsinh} y_{0}.} 由于双曲正弦函数在实数域上严格单调递增,所以反双曲正弦函数存在、单值且严格单调递增。有这样的类似讨论,可以得到另外五种双曲三角函数的反函数。注意,双曲余弦和双曲正割是偶函数,它们的反函数是二值的,因此我们一般选择它们原来函数的正数部分取反函数。 对于每个函数的讨论详见具体的函数介绍页面,以下是结论。 名称 定义与解析表达 定义域 值域 图像 反双曲正弦 arsinh x = ln ( x + x 2 + 1 ) {\displaystyle \operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)} R {\displaystyle \mathbb {R} } R {\displaystyle \mathbb {R} }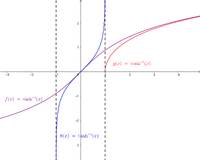 反双曲余弦
arcosh
x
=
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)}
x
>
1
{\displaystyle x>1}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
反双曲正切
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\dfrac {1}{2}}\ln \left({\dfrac {1+x}{1-x}}\right)}
|
x
|
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\dfrac {1}{2}}\ln \left({\dfrac {x+1}{x-1}}\right)}
|
x
|
>
1
{\displaystyle |x|>1}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
反双曲余弦
arcosh
x
=
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)}
x
>
1
{\displaystyle x>1}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
反双曲正切
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\dfrac {1}{2}}\ln \left({\dfrac {1+x}{1-x}}\right)}
|
x
|
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\dfrac {1}{2}}\ln \left({\dfrac {x+1}{x-1}}\right)}
|
x
|
>
1
{\displaystyle |x|>1}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
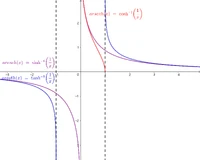 反双曲正割
arsech
x
=
ln
(
1
x
+
1
x
2
−
1
)
{\displaystyle \operatorname {arsech} x=\ln \left({\dfrac {1}{x}}+{\sqrt {{\dfrac {1}{x^{2}}}-1}}\right)}
(
0
,
1
]
{\displaystyle (0,1]}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
反双曲余割
arcsch
x
=
ln
(
1
x
+
1
x
2
+
1
)
{\displaystyle \operatorname {arcsch} x=\ln \left({\dfrac {1}{x}}+{\sqrt {{\dfrac {1}{x^{2}}}+1}}\right)}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
反双曲正割
arsech
x
=
ln
(
1
x
+
1
x
2
−
1
)
{\displaystyle \operatorname {arsech} x=\ln \left({\dfrac {1}{x}}+{\sqrt {{\dfrac {1}{x^{2}}}-1}}\right)}
(
0
,
1
]
{\displaystyle (0,1]}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
反双曲余割
arcsch
x
=
ln
(
1
x
+
1
x
2
+
1
)
{\displaystyle \operatorname {arcsch} x=\ln \left({\dfrac {1}{x}}+{\sqrt {{\dfrac {1}{x^{2}}}+1}}\right)}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
最主要的是前三个,后三个可以借由复合函数来定义。 它们推广到复变函数的情形后都变为多值函数,而上述定义仍然适用,只是此时的根式以及对数函数都变为多值函数,当对数函数和根式函数都取主值且函数为实变量的时候,就恢复到了通常定义下的实变量反双曲函数。 双曲复合[]像三角复合问题一样,有时候我们在积分中做了双曲代换,但最后又不得不回代原变量,尤其是不定积分情形,这时我们就要解决类似 x = sinh t , cosh t = ? ? ? {\displaystyle x=\sinh t,\cosh t=???} 的问题,三角代换情形可以使用直角三角形辅助,也可使用三角函数线,对应双曲情形也可以使用单位双曲线的右支——即双曲函数线解决,当然也可以用反双曲函数的对数定义,再用双曲函数的指数定义。 函数 sinh t = {\displaystyle \sinh t=} cosh t = {\displaystyle \cosh t=} tanh t = {\displaystyle \tanh t=} x = sinh t {\displaystyle x=\sinh t} x {\displaystyle x} x 2 + 1 {\displaystyle {\sqrt {x^{2}+1}}} x x 2 + 1 {\displaystyle {\dfrac {x}{\sqrt {x^{2}+1}}}} x = cosh t {\displaystyle x=\cosh t} x 2 − 1 {\displaystyle {\sqrt {x^{2}-1}}} x {\displaystyle x} x 2 − 1 x {\displaystyle {\dfrac {\sqrt {x^{2}-1}}{x}}} x = tanh t {\displaystyle x=\tanh t} x 1 − x 2 {\displaystyle {\dfrac {x}{\sqrt {1-x^{2}}}}} 1 1 − x 2 {\displaystyle {\dfrac {1}{\sqrt {1-x^{2}}}}} x {\displaystyle x}这里仅列出九个主要的,其余都可以用复合函数化为上表的类型,不过要特别注意如下从根式中提取 x {\displaystyle x} 的操作的符号问题: cosh ( arcoth x ) = cosh ( artanh 1 x ) = 1 1 − ( 1 x ) 2 = | x | x 2 − 1 . {\displaystyle \cosh(\operatorname {arcoth} x)=\cosh \left(\operatorname {artanh} {\dfrac {1}{x}}\right)={\dfrac {1}{\sqrt {1-\left({\frac {1}{x}}\right)^{2}}}}={\dfrac {|x|}{\sqrt {x^{2}-1}}}.} 微分[]这里仅列出主要结果,它们导数的推导可以依照反函数求导法则完成。 d d x arsinh x = 1 x 2 + 1 , d d x arcosh x = 1 x 2 − 1 , d d x artanh x = 1 1 − x 2 , d d x arcoth x = 1 1 − x 2 , d d x arsech x = − 1 x 1 − x 2 , d d x arcsch x = − 1 | x | 1 + x 2 . {\displaystyle {\begin{aligned}&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arsinh} x={\dfrac {1}{\sqrt {x^{2}+1}}},&&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcosh} x={\dfrac {1}{\sqrt {x^{2}-1}}},\\&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {artanh} x={\dfrac {1}{1-x^{2}}},&&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcoth} x={\dfrac {1}{1-x^{2}}},\\&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arsech} x=-{\dfrac {1}{x{\sqrt {1-x^{2}}}}},&&{\dfrac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcsch} x=-{\dfrac {1}{|x|{\sqrt {1+x^{2}}}}}.\end{aligned}}}以上求导公式逆用(为凑微分)时不能在反双曲函数没有定义的不连续点上进行。这些公式在复变场合依然成立(注意主值支的选取),因此也有用如上公式之逆——变限积分,来定义对应的双曲函数的。 积分[]这里仅列出主要结果,它们求积分可以用双曲代换和分部积分完成。以下我们给出了做双曲代换的中间过程,便于推导(这绝不提倡直接记忆结果), x {\displaystyle x} 和 t {\displaystyle t} 的关系是对应被积函数的反函数,如在第一个中就是 x = sinh t . {\displaystyle x=\sinh t.} ∫ arsinh x d x = t sinh t − cosh t + C = x arsinh x − x 2 + 1 + C . ∫ arcosh x d x = t cosh t − sinh t + C = x arcosh x − x 2 − 1 + C . ∫ artanh x d x = t tanh t − ln cosh t + C = x artanh x + 1 2 ln ( 1 − x 2 ) + C . ∫ arcoth x d x = t coth t − ln | sinh t | + C = x arcoth x + 1 2 ln ( x 2 − 1 ) + C . ∫ arsech x d x = t sech t − arctan ( sinh t ) + C = x arsech x + arcsin x + C . ∫ arcsch x d x = t csch t − ln | tanh t 2 | + C = x arcsch x + | arsinh x | + C . {\displaystyle {\begin{aligned}&\int \operatorname {arsinh} x\mathrm {d} x=t\sinh t-\cosh t+C&&=x\operatorname {arsinh} x-{\sqrt {x^{2}+1}}+C.\\&\int \operatorname {arcosh} x\mathrm {d} x=t\cosh t-\sinh t+C&&=x\operatorname {arcosh} x-{\sqrt {x^{2}-1}}+C.\\&\int \operatorname {artanh} x\mathrm {d} x=t\tanh t-\ln \cosh t+C&&=x\operatorname {artanh} x+{\dfrac {1}{2}}\ln(1-x^{2})+C.\\&\int \operatorname {arcoth} x\mathrm {d} x=t\coth t-\ln |\sinh t|+C&&=x\operatorname {arcoth} x+{\dfrac {1}{2}}\ln(x^{2}-1)+C.\\&\int \operatorname {arsech} x\mathrm {d} x=t\operatorname {sech} t-\arctan(\sinh t)+C&&=x\operatorname {arsech} x+\arcsin x+C.\\&\int \operatorname {arcsch} x\mathrm {d} x=t\operatorname {csch} t-\ln \left|\tanh {\dfrac {t}{2}}\right|+C&&=x\operatorname {arcsch} x+|\operatorname {arsinh} x|+C.\\\end{aligned}}}以上作定积分时不能跨越反双曲函数的奇点(不连续点)。 级数展开[]只有将函数放到复平面上,级数展开的操作才会变得更加明朗。以下级数展开为洛朗级数(前两个为泰勒级数)。 arsinh x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n − 1 ) ! ! ( 2 n ) ! ! ( 2 n + 1 ) x 2 n + 1 = x − x 3 6 + 3 x 5 40 − 5 x 7 112 + ⋯ , ∀ x : | x | n = 0 ∞ 1 2 n + 1 x 2 n + 1 = x + x 3 3 + x 5 5 + x 7 7 , ∀ x : | x | n = 0 ∞ ( − 1 ) n ( 2 n − 1 ) ! ! ( 2 n ) ! ! ( 2 n + 1 ) x − 2 n − 1 = 1 x − 1 6 x 3 + 3 40 x 5 − 5 112 x 7 + ⋯ , ∀ x : | x | > 1 , arcoth x = ∑ n = 0 ∞ 1 2 n + 1 x − 2 n − 1 = 1 x + 1 3 x 3 + 1 5 x 5 + 1 7 x 7 , ∀ x : | x | > 1. {\displaystyle {\begin{aligned}\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n-1)!!}{(2n)!!(2n+1)}}x^{2n+1}&&=x-{\dfrac {x^{3}}{6}}+{\dfrac {3x^{5}}{40}}-{\dfrac {5x^{7}}{112}}+\cdots ,&&\forall x:|x|1.\end{aligned}}}注意到这些反函数均是多值的,因此考虑到复变情形时上述展开只是在主值支上的展开,注意:反双曲余弦和反双曲正割不能在复平面上洛朗展开,因为要展开的点——原点是这两个多值函数的支点。 参见[] 双曲恒等式 双曲积分 三角函数 反三角函数 三角恒等式 三角积分 复指数函数 |
【本文地址】
 给定一个确定的
y
0
∈
R
{\displaystyle y_{0}\in \mathbb {R} }
给定一个确定的
y
0
∈
R
{\displaystyle y_{0}\in \mathbb {R} }
 ,方程
sinh
x
=
y
0
{\displaystyle \operatorname {sinh} x=y_{0}}
,方程
sinh
x
=
y
0
{\displaystyle \operatorname {sinh} x=y_{0}}
 的解
x
=
x
0
{\displaystyle x=x_{0}}
的解
x
=
x
0
{\displaystyle x=x_{0}}
 就称作
y
0
{\displaystyle y_{0}}
就称作
y
0
{\displaystyle y_{0}}
 的反双曲正弦,记作
x
0
=
arsinh
y
0
.
{\displaystyle x_{0}=\operatorname {arsinh} y_{0}.}
的反双曲正弦,记作
x
0
=
arsinh
y
0
.
{\displaystyle x_{0}=\operatorname {arsinh} y_{0}.}

 R
{\displaystyle \mathbb {R} }
R
{\displaystyle \mathbb {R} }
 R
{\displaystyle \mathbb {R} }
R
{\displaystyle \mathbb {R} }
 x
>
1
{\displaystyle x>1}
x
>
1
{\displaystyle x>1}
 [
0
,
+
∞
)
{\displaystyle [0,+\infty )}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
 反双曲正切
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\dfrac {1}{2}}\ln \left({\dfrac {1+x}{1-x}}\right)}
反双曲正切
artanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {artanh} x={\dfrac {1}{2}}\ln \left({\dfrac {1+x}{1-x}}\right)}
 |
x
|
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\dfrac {1}{2}}\ln \left({\dfrac {x+1}{x-1}}\right)}
|
x
|
(
x
+
1
x
−
1
)
{\displaystyle \operatorname {arcoth} x={\dfrac {1}{2}}\ln \left({\dfrac {x+1}{x-1}}\right)}
 |
x
|
>
1
{\displaystyle |x|>1}
|
x
|
>
1
{\displaystyle |x|>1}
 R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}

 (
0
,
1
]
{\displaystyle (0,1]}
(
0
,
1
]
{\displaystyle (0,1]}
![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4) [
0
,
+
∞
)
{\displaystyle [0,+\infty )}
[
0
,
+
∞
)
{\displaystyle [0,+\infty )}
 R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
R
−
{
0
}
{\displaystyle \mathbb {R} -\{0\}}
 的问题,三角代换情形可以使用直角三角形辅助,也可使用三角函数线,对应双曲情形也可以使用单位双曲线的右支——即双曲函数线解决,当然也可以用反双曲函数的对数定义,再用双曲函数的指数定义。
的问题,三角代换情形可以使用直角三角形辅助,也可使用三角函数线,对应双曲情形也可以使用单位双曲线的右支——即双曲函数线解决,当然也可以用反双曲函数的对数定义,再用双曲函数的指数定义。
 cosh
t
=
{\displaystyle \cosh t=}
cosh
t
=
{\displaystyle \cosh t=}
 tanh
t
=
{\displaystyle \tanh t=}
tanh
t
=
{\displaystyle \tanh t=}
 x
=
sinh
t
{\displaystyle x=\sinh t}
x
=
sinh
t
{\displaystyle x=\sinh t}
 x
{\displaystyle x}
x
{\displaystyle x}
 x
2
+
1
{\displaystyle {\sqrt {x^{2}+1}}}
x
2
+
1
{\displaystyle {\sqrt {x^{2}+1}}}
 x
x
2
+
1
{\displaystyle {\dfrac {x}{\sqrt {x^{2}+1}}}}
x
x
2
+
1
{\displaystyle {\dfrac {x}{\sqrt {x^{2}+1}}}}
 x
=
cosh
t
{\displaystyle x=\cosh t}
x
=
cosh
t
{\displaystyle x=\cosh t}
 x
2
−
1
{\displaystyle {\sqrt {x^{2}-1}}}
x
2
−
1
{\displaystyle {\sqrt {x^{2}-1}}}
 x
{\displaystyle x}
x
{\displaystyle x}
 x
=
tanh
t
{\displaystyle x=\tanh t}
x
=
tanh
t
{\displaystyle x=\tanh t}
 x
1
−
x
2
{\displaystyle {\dfrac {x}{\sqrt {1-x^{2}}}}}
x
1
−
x
2
{\displaystyle {\dfrac {x}{\sqrt {1-x^{2}}}}}
 1
1
−
x
2
{\displaystyle {\dfrac {1}{\sqrt {1-x^{2}}}}}
1
1
−
x
2
{\displaystyle {\dfrac {1}{\sqrt {1-x^{2}}}}}
 x
{\displaystyle x}
x
{\displaystyle x}
 微分[]
微分[]

 的关系是对应被积函数的反函数,如在第一个中就是
x
=
sinh
t
.
{\displaystyle x=\sinh t.}
的关系是对应被积函数的反函数,如在第一个中就是
x
=
sinh
t
.
{\displaystyle x=\sinh t.}


