[论文精读] SIGGRAPH 2020: 基于常曲率度量的曲面间几何映射

Patrick Schmidt, Marcel Campen, Janis Born, Leif Kobbelt

RWTH Aachen University, Osnabrück University

Project Page

计算机图形学，几何处理、建模与优化，微分几何

几何映射是计算机图形学、几何处理与建模领域非常基本的工具。这篇文章主要提出了一种构建两个亏格（genus）相同的离散曲面间的几何映射的良好算法。

这里首先介绍一下几何处理领域中几何映射的几个重要性质：

前两个性质要么同时满足，要么都不满足；当它们同时满足时,称这个几何映射是同胚（surface homeomorphism）的。

先前关于曲面间几何映射的一些工作，包括：

而本论文提出的曲面间几何映射，在保证连续性与双射性的前提下，该映射的不同之处在于：

假设我们要寻找如下两个开网格之间的对应映射关系，有一种方法是将它们都参数化至同一平面区域（如圆盘），就很容易寻找它们的对应覆盖关系（简称surfsace-to-plane），由平面区域这个参数空间出发，根据参数空间映射到两个3D网格空间各自的Jocabi，构建如下能量函数最小化（类似SD能量/对称狄利克雷能量，Symmetric Dirichlet）。

但对于更一般的闭网格，我们无法直接对其做参数化，而surface-to-surface的对应关系比surfsace-to-plane的对应关系要复杂得多。尽管点与点的对应可以由目标曲面上的三角面片顶点的重心坐标来简单地获得，但点之间相连的边的关系，在surfsace-to-plane情形下很容易通过目标曲面上的顶点的线性插值隐式地获取，然而surface-to-surface情形下存在不确定性，如下图所示。

比较常见的解决方法是利用目标曲面上两点之间的最短测地线来定义其相连的边，但这种方式并不稳定。首先离散曲面上的测地线并不唯一，其次它并不是随着端点的变化而连续变化的——也就是说，可能在微小地移动某点后，相应的最小测地线可能完全就不同了。这在优化上是一个非常困难的问题。

而本论文就提出了一种边在目标曲面上的像的良好定义，它是隐式表示的、唯一的，且随着点的变化而连续变化的。

确定这种边在目标曲面上的像的定义是本文的关键问题。有了这种定义，我们就可以仅仅将顶点作为优化变量，计算一个连续优化问题。而确定了边在目标曲面上的像之后，就确定了目标曲面上的一个由多条线段构成的“三角形”，那么该“三角形”内部区域的计算就可以全部利用分片线性映射（picewise linear）来解决，这一步就比较容易。

接下来我们详细介绍如何定义上述边在目标曲面上的像（可能会比较难理解，会涉及一些微分几何的思想和概念，我会尽量讲清楚）：

首先，我们知道（连续意义下）曲面上的测地线是由该曲面的度量（metric）决定的，它描述了在某种度量下，（连续）曲面上某一点往各个确定的方向移动所需要的代价。（下图中画的是离散情形，但实际上这个定义是通用的）

在三角网格曲面上，我们可以将这种度量视为每个三角形的固有、本质的一种形状特性，例如我们可以对每条边 e 都定义一个“虚拟的长度” l(e) ，称之为“虚拟”是因为一般我们都用最常见的欧式度量，即用欧式距离来描述一条边的长度，但实际上还可以有更多距离的定义方式。相当于我们不改变拓扑连接关系，而改变了边长度，由此整个网格的所有边都有了这种新的长度定义，并进一步决定了该度量空间中相应的测地线是如何的。

我们的基本思路是将目标曲面映射到平面（如下左图）上并计算测地线，因为平面上的测地线就是直线段，唯一定义并容易计算。我们的基本方法是“仿造一个具有该种性质的平面”，也就是给曲面赋予一个平坦度量flat metric（高斯曲率恒为0），使得该曲面patch内每个顶点处的离散曲率为0（如下右图中的绿点），那么整个曲面patch上的曲率处处为0，这样目标曲面上的测地线就是唯一的，因为它就是平面上的一条条直线段。

从全局一致性上考虑，对一般的闭曲面来说为它赋予一个平坦度量通常是不可能的，Gauss-Bonnet定理直接说明了这一点，只有亏格为1才可以使用平坦度量。为了适用于其他亏格的情形，我们将“曲率处处为0”这个思想推广为“曲率处处为常数”，也就是由平面度量推广到球面度量（spherical metric）、双曲度量（hyperbolic metric），寻找到球面、双曲面的同胚映射。

这里需要说明一点，球面与平面都是可以无扭曲损失地嵌入欧式空间的，但双曲度量下的情形并不能，无论是庞加莱（Poincare）模型、克莱因（Klein）模型还是双曲面（Hyperboloid）模型。本论文采用第三种双曲面（Hyperboloid）模型（为了定义的一致性，下文会提到），下图表示的是它的一个剖面。论文提出了如下公式来计算无扭曲损失地边长：

d(p,q)=arccos(-_M)

在具体计算上，我们通过解离散曲面上的偏微分方程问题（PDE）或直接在球面/平面/双曲面这三个基本模型流形上构建。

首先是如何计算测地线——对于球面与双曲面的情形，测地线都定义为过原点的平面与它们相交所截成的交线。 对于平面情形，为了一致性的定义，我们将 xOy 平面移动至 z=1 处，然后采用相同的定义构建方式。（如下图中间所示，白色为 z=1 的坐标平面，蓝色为过原点的截面）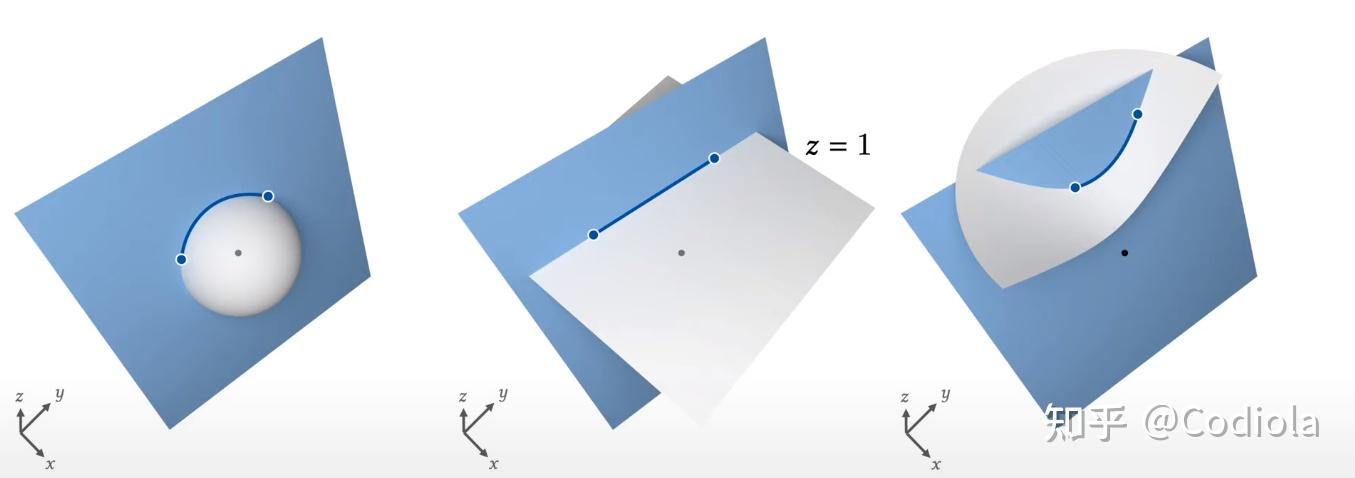

其次是如何计算两条测地线段的交点——这很显然，它就是由两个截面所截成的两条测地线的交。三种情形的计算公式都是相同的。注意，这里需要选取相同的曲线参数化，以方便存储交点的参数，论文中给出了一种利用中心投影的构建方式，详见论文。

现在回到我们的关键问题：确定边在目标曲面上的像。

这里还存在最后一个问题：度量下的最短测地线真的是唯一的吗？如下图的亏格为1的例子中，红、蓝、绿三条都是“度量下长度相同”的最短测地线（尽管视觉看起来不同长度）。论文中引入了不同路径同伦类（path homotopy）的三角网格带，并在优化中予以自动考虑、选择哪条三角网格带，详见论文。

终于，我们可以如下唯一地表示所提出的映射 (\phi,h,l) ：

另外，由于本论文提出的映射是一个双射，反过来从（原先定义的）目标曲面到输入曲面的逆映射该如何计算呢？

文章提出了一个Completion算子，大致思路是构造一个基于输入网格与目标网格上所有顶点以及边与测地线交点的覆盖镶嵌，它以相同的拓扑连接关系存在于这两个网格上，里面包含了三角形、凸四边形、凸五边形、凸六边形，如下图所示。

在内部，对于两个边数相同的凸多边形，定义边界上的双射是显然的，至于内部的双射，论文用一种简单的评估与优化策略来生成相应的三角化，由此转化为三角形之间的双射。

这样我们就利用Completion算子，通过公共的覆盖镶嵌，在整个网格上实现了分片线性映射。这种方式的好处很多，比如对某些含有缝隙的纹理，在映射到目标曲面后缝隙边是仍然存在的（很多方法并不能做到这点）；同时，它也有一些问题，就是覆盖镶嵌后的计算量确实增大了，但是我们也可以根据具体应用场景，再仍然保持双射性的同时再将网格粗化。

有了映射 (\phi,h,l) ，就需要通过最小化能量函数，来优化 \phi,h,l 这三个量，下图表示优化的简单流程：

结果展示1：下图是将高扭曲的初始映射优化为低扭曲的过程，右上角是其SD能量的分布图：

结果展示2：下图是通过若干个landmarks约束由不同算法计算出的映射结果与相应的SD能量分布图。可以看到，在约束点选取合理的情况下，各算法的表现都相对较好。但当移除其中一个landmarks后，HOT算法尽管由于其算法本身保证了双射性与光滑性，但在移除点的附近扭曲较高；RHM算法由于算法本身是嵌入的，因此双射性不能保证，且扭曲也比较大；而本文的算法效果则好于前两者。

结果展示3：这是另一个没有landmarks的例子，本论文的效果也表现最好。右图是SD能量低于某个阈值的区域占比。

结果展示4：在如下例子中可以发现，相比其他算法，本论文的方法能够将那些不可避免的扭曲损失尽可能均匀地平摊到整个模型上。

结果展示5：对于一些高亏格的模型，本论文的方法可以先用landmarks约束保证获得一个较好的初始化，然后在具体优化的过程中去掉它们，而这在HOT算法中是无法实现的。

结果展示6：在一些特定的场景，例如下图的艺术化创作，landmarks的选择可能并非为了最小化扭曲损失，而是出于某些艺术角度的考量。

结果展示7：该算法对于一些较差的初始化（与所需情形相差甚远），也能得到较好的结果。当然，这并非绝对的（所以自动化地寻找局部最优条件是一个很有趣的问题）。

其他相关论文：