| 结构方程模型1(总要) | 您所在的位置:网站首页 › 模型残差项 › 结构方程模型1(总要) |
结构方程模型1(总要)
|
结构方程模型1(总要)
SEM在估计一组观察变量与其代表的潜变量、因子的关系的同时,分析各潜变量之间的关系,这样潜变量之间的关系估计不受测量误差的影响。 SEM的有点:具有同时对多个因变量建模的能力;检验模型的整体拟合度;检验直接效应、间接效应和总体效应;检验复杂与特定假设;检验跨组参数恒定性;处理复杂数据(如带自相关误差的时间序列数据、非正态分布数据、截断数据以及分类输出数据) 结构方程建模过程: 模型表述:模型估计之前形成的最初理论模型。是在理论研究或实践经验的基础上形成的; 模型识别:决定设定模型的参数估计是否有唯一解。如果错误设定,模型估计可能不收敛或无解。 模型估计:最常用的是最大似然估计。 模型评估:需要评估模型是否拟合数据。 模型修正:如果拟合不好,需要重新设定或修改模型。需要决定如何删除、增加或修改模型中的参数。 1.1 模型表述Model formulation最直接的方法是路径图path diagram来描述研究员感兴趣的模型。正方形或者长方形表示观察变量、观察变量也称为测量变量、外显变量或外显标识。圆或椭圆表示潜变量或因子。变量之间的关系用线条表示。单向箭头表示两变量之间具有效应关系,箭头所指的变量受另一个变量的影响。双向箭头表示变量之间具有关联,但不表示变量之间的效应。 基本目的是描述观察标识变量是否适合作为潜变量或因子的测量手段。建立观察标识变量与其所测量的潜变量之间的联系或关系,然后用数据检验是否存在假设的因子结构。 结构模型评估潜变量之间的相互关系。结构方程模型中各潜变量之间的关系是与测量模型同时估计的。如果结构模型中的变量都是观察变量而不是潜变量,那么结构方程就会变成一组观察变量之间结构关系的建模体系。 上图模型是一个递归模型。如果模型具有回馈效应或反馈效应,即 η 1 \eta_1 η1与 η 2 \eta_2 η2相互影响即互为因果关系,则该模型称为非递归模型,一般只讨论递归模型。 1.1.3 模型表达方程Model formulation in equations一般结构方程可用3个基本方程表达: η = B η + Γ ξ + ζ \eta=B\eta+\Gamma\xi+\zeta η=Bη+Γξ+ζ Y = Λ y η + ϵ Y=\Lambda_y\eta+\epsilon Y=Λyη+ϵ X = Λ x ξ + δ X=\Lambda_x\xi+\delta X=Λxξ+δ 一般结构方程模型的3个基本方程中变量矩阵的定义 变量定义维度 η \eta η内生潜变量 m × 1 m\times1 m×1 ξ \xi ξ外源潜变量 n × 1 n\times1 n×1 ζ \zeta ζ方程中的干扰项 m × 1 m\times1 m×1 y y y内生标识 p × 1 p\times1 p×1 x x x外源标识 q × 1 q\times1 q×1 ϵ \epsilon ϵ y y y的测量误差 p × 1 p\times1 p×1 δ \delta δ x x x的测量误差 q × 1 q\times1 q×1
SEM模型识别的必要条件: 数据点的数量不能少于自由参数的数量,自由度不能为负。数据点数是观察变量的方差/协方差矩阵的不同元素的数量,等于 ( p + q ) / ( p + q + 1 ) / 2 (p+q)/(p+q+1)/2 (p+q)/(p+q+1)/2。自由参数的数量是模型所要估计的参数数量,包括因子负载、路径系数、潜变量方差、协方差及误差项方差、协方差等。如果数据点数超过自由参数的数量,模型称为超识别模型overidentified model;如果数据点数少于自由参数的数量,模型称为欠识别模型under identified model,欠识别模型无法估计模型参数。数据点等于自由参数的数量,模型称为恰识别模型just identified model。自由度为零的模型能够进行模型参数估计无法进行模型拟合优度检验。 模型每一个潜变量都必须设定一个测量尺度。有两种方式:一是将一个观察标识的因子载荷固定为一个常数通常为1;二是将潜变量的方差固定为1即潜变量标准化。 于放模型识别问题发生的重点在于参数设定。取决于如何将参数设定为自由参数free parameter、固定参数fixed parameter或强制参数constrained parameter。 1.3 模型估计Model estimation结构方程模型的估计是极小化样本方差/协方差与模型估计的方差/协方差之间的关系。用 Σ \Sigma Σ代表观察变量 y 和 x y和x y和x的总体方差/协方差矩阵,结构方差模型估计的关键点是可以将矩阵 Σ \Sigma Σ表达为假定模型中自由参数 θ \theta θ的函数,分析的基本假设是: Σ = Σ ( θ ) \Sigma=\Sigma(\theta) Σ=Σ(θ) Σ ( θ ) \Sigma(\theta) Σ(θ)为模型估计的方差/协方差矩阵,也称模型隐含的方差/协方差矩阵,是假设模型的总体参数所暗示的方差/协防太差矩阵。模型估计或拟合的目的是找到一组模型参数 θ \theta θ,计算 Σ ( θ ) \Sigma(\theta) Σ(θ),并使 Σ − Σ ( θ ) \Sigma-\Sigma(\theta) Σ−Σ(θ)最小化。 由于 Σ \Sigma Σ与 Σ ( θ ) \Sigma(\theta) Σ(θ)未知,因此实际上是最小化 S − Σ ( θ ^ ) S-\Sigma(\hat\theta) S−Σ(θ^)或 S − Σ ^ S-\hat\Sigma S−Σ^。 θ ^ \hat\theta θ^是模型样本参数估计值, Σ ^ \hat\Sigma Σ^是从样本估计的模型隐含方差/协方差矩阵。一般结构方程模型由8个参数矩阵的各固定与自由参数的特定模式所表示。观察方差/协方差矩阵用于估计参数矩阵中的自由参数值,使其能最好的再生出 Σ ^ \hat\Sigma Σ^,并使 Σ ^ \hat\Sigma Σ^与 S S S的差别最小化。 模型估计过程中须用一种特殊拟合函数以尽可能地减少 S S S与 Σ ^ \hat\Sigma Σ^之间的差异,最常见的是似然函数; F M L ( θ ^ ) = l n ∣ Σ ^ ∣ − l n ∣ S ∣ + t r ( S Σ ^ − 1 ) − ( p + q ) F_{ML}(\hat\theta)=ln|\hat\Sigma|-ln|S|+tr(S\hat\Sigma^{-1})-(p+q) FML(θ^)=ln∣Σ^∣−ln∣S∣+tr(SΣ^−1)−(p+q) F M L F_{ML} FML是对差异函数的测量,称为最小差异函数。一个完美拟合的模型,最小差异函数为零。 结构方程模型估计以最大似然估计为基础。第一,ML估计是无偏估计;第二,ML估计具有一致性;第三,ML具有渐近有效性;第四,ML估计具有渐近正态性。这样可以进行假设的显著性检验和计算参数的置信区间;第五,ML函数不受限于变量的测量尺度。在多元正态和大样本假设下,ML拟合函数 F M L ( θ ^ ) F_{ML}(\hat\theta) FML(θ^)乘 n − 1 n-1 n−1接近卡方分布。 ML估计法适用于正态分布下得连续结局测量变量,在数据非正态分布情况下,虽然ML参数估计值不易出现偏倚,但是参数估计值的标准误可能会出现偏倚。传统的补救措施有:将变量的非正态分布转化为近似正态分布;去除数据中的异常值;使用自助法估计参数。但广泛用于SEM中处理非正态数据、比传统方法更好的方法是应用无须假设正态分布的稳健估计法估计模型。 关于估计有以下主要几种方法。渐近五分不估计法asymptotically distribution free estimator ADF,是大样本情况下无须考虑变量分布的参数稳健估计方法,以样本方差/写防擦和矩阵S各元素的方差/协方差和峰度对ADF函数加权,并以此调整数据的多元非正态性。缺点是当观察变量数量较大时需要很大的样本量来估计其权重矩阵,且计算非常耗时,若样本量不足,则会产生很大偏度,导致ADF的权重不可逆。 1.4 模型评估Model evaluation多种方法可用于评估 S S S与 Σ ^ \hat\Sigma Σ^之间的接近程度,因此有多种模型拟合指数,可以分为两大类:绝对拟合指数absolute fit indices和增值拟合指数incremental fit indices. 绝对拟合指数:直接评估设定模型与样本数据的拟合情况。实际上是将设定模型与饱和模型进行比较的,饱和模型精确拟合数据,隐含矩阵和观察矩阵相等。包括模拟卡方统计、拟合优度指数、调整拟合优度指数、残差均方根、标化残差均方根、近似误差均方根。 增值拟合指数:比较设定模型与基准模型或独立模型,检测模型拟合相对基准模型而言改善的比例。基准模型是数据拟合最差的模型,只容许观察变量方差而没有反映各变量之间关系的协方差,因此零模型中没有潜变量。包括:规范拟合指数、增值拟合指数、非规范指数、相对离中指数、比较拟合指数。 模型拟合指数也可划分为离中指数、简约调整拟合指数和信息标准指数。 离中指数:传统检验法通过检验卡方和 p p p值了解模型拟合度,离中指数评估模型不拟合数据的程度。离中指数以离中参数nocentrality parameter NCP为基础,可以估计为 χ 2 − d f ( 如 χ 2 ; d f , 则 χ 2 − d f = 0 ) \chi^2-df(如\chi^2;df,则\chi^2-df=0) χ2−df(如χ2 |
【本文地址】
 模型内变量决定的潜变量或因子称为内生潜变量endogenous latent variables,用
η
\eta
η表示,如果潜变量的原因基于模型之外,称为外源潜变量exogenous latent variables,用
ξ
\xi
ξ。外源潜变量的表示称为外源标识exogenous indicator,内生潜变量的标识称为内生标识endogenous indicator。用
δ
\delta
δ标识前者的测量误差项,用
ϵ
\epsilon
ϵ标识后者的测量误差项。
β
\beta
β和
γ
\gamma
γ是路径系数path coefficients。下标第一个数字代表内生因变量,第二个下标代表原因变量,可以是内生变量,也可以是外源变量。 如果原因变量为外源变量,则路径系数用
γ
\gamma
γ表示,如果原因变量为内生变量,则路径系数用
β
\beta
β表示。
ζ
\zeta
ζ表示结构方程的残差项。 结构方程模型分析的重点是潜变量或因子,而不是观察变量。目的是提供一种不受测量误差影响的手段来估计设定模型中潜变量间的结构关系。将测量模型measurement model(或验证性因子分析confirmatory factor analysis analysis,CFA)和结构方程structural equations(或潜变量模型latent cariable model)整合在一个结构方程模型框架内就能实现该目的。
模型内变量决定的潜变量或因子称为内生潜变量endogenous latent variables,用
η
\eta
η表示,如果潜变量的原因基于模型之外,称为外源潜变量exogenous latent variables,用
ξ
\xi
ξ。外源潜变量的表示称为外源标识exogenous indicator,内生潜变量的标识称为内生标识endogenous indicator。用
δ
\delta
δ标识前者的测量误差项,用
ϵ
\epsilon
ϵ标识后者的测量误差项。
β
\beta
β和
γ
\gamma
γ是路径系数path coefficients。下标第一个数字代表内生因变量,第二个下标代表原因变量,可以是内生变量,也可以是外源变量。 如果原因变量为外源变量,则路径系数用
γ
\gamma
γ表示,如果原因变量为内生变量,则路径系数用
β
\beta
β表示。
ζ
\zeta
ζ表示结构方程的残差项。 结构方程模型分析的重点是潜变量或因子,而不是观察变量。目的是提供一种不受测量误差影响的手段来估计设定模型中潜变量间的结构关系。将测量模型measurement model(或验证性因子分析confirmatory factor analysis analysis,CFA)和结构方程structural equations(或潜变量模型latent cariable model)整合在一个结构方程模型框架内就能实现该目的。 λ
\lambda
λ称为因子负载,表示观察变量与潜变量之间的关系。实际上是将观察变量作为因变量,相关潜变量作为自变量的线性回归系数。
ϕ
12
\phi_{12}
ϕ12表示
ξ
1
\xi_1
ξ1与
ξ
2
\xi_2
ξ2的协方差,但不表示因果关系。如果两个潜变量之间没有相关关系,则
ϕ
12
=
0
\phi_{12}=0
ϕ12=0。对于单因子CFA模型,模型识别至少需要有3个标识,而且误差项不能相关。图1.1.1-2所示的单因子验证性因子模式是恰识别的just identified,观察变量的方差/协方差的数量(6)等于自由参数的数量(2个自由因子负载,3个误差项方差和1个因子方差)。但是能估计模型的参数不饿能评估模型拟合数据的情况。为了评估模型的拟合度模型必须是超识别的overidentified,观察和数据点数要大于模型估计的自由参数总数。CFA有多因子且特定因子至少与另一个因子相关但误差项不相关,那么可以只有两个测量标识。
λ
\lambda
λ称为因子负载,表示观察变量与潜变量之间的关系。实际上是将观察变量作为因变量,相关潜变量作为自变量的线性回归系数。
ϕ
12
\phi_{12}
ϕ12表示
ξ
1
\xi_1
ξ1与
ξ
2
\xi_2
ξ2的协方差,但不表示因果关系。如果两个潜变量之间没有相关关系,则
ϕ
12
=
0
\phi_{12}=0
ϕ12=0。对于单因子CFA模型,模型识别至少需要有3个标识,而且误差项不能相关。图1.1.1-2所示的单因子验证性因子模式是恰识别的just identified,观察变量的方差/协方差的数量(6)等于自由参数的数量(2个自由因子负载,3个误差项方差和1个因子方差)。但是能估计模型的参数不饿能评估模型拟合数据的情况。为了评估模型的拟合度模型必须是超识别的overidentified,观察和数据点数要大于模型估计的自由参数总数。CFA有多因子且特定因子至少与另一个因子相关但误差项不相关,那么可以只有两个测量标识。
 结构方程模型的设定实际上是通过对这8个矩阵中的参数具体设定来表述的。这些参数可以设定为固定参数fixed parameter,也可以设定为自由参数free parameter。固定参数不能由数据估计,值通常固定为0(如协方差为零或斜率为零,表示无相关关系或效应),或1(如因模型识别的需要,通常,每个因子须有一个因子载荷设定为0)。 方程
η
=
B
η
+
Γ
ξ
+
ζ
\eta=B\eta+\Gamma\xi+\zeta
η=Bη+Γξ+ζ的矩阵表示为:
(1.1.3-2)
[
η
1
η
2
]
=
[
0
β
12
0
0
]
[
η
1
η
2
]
+
[
γ
11
γ
12
γ
21
γ
22
]
+
[
ζ
1
ζ
2
]
\left[ \begin{matrix} \eta_1 \\ \eta_2 \end{matrix} \right]=\left[ \begin{matrix} 0 ; \beta_{12}\\ 0 ; 0 \end{matrix} \right]\left[ \begin{matrix} \eta_1\\ \eta_2 \end{matrix} \right]+ \left[ \begin{matrix} \gamma_{11} ; \gamma_{12} \\ \gamma_{21} ; \gamma_{22} \end{matrix} \right]+ \left[ \begin{matrix} \zeta_1\\ \zeta_2 \end{matrix} \right]\tag{1.1.3-2}
[η1η2]=[00β120][η1η2]+[γ11γ21γ12γ22]+[ζ1ζ2](1.1.3-2) 图1.1-2所示模型可以导出以下两个结构方程
η
1
=
β
12
η
2
+
γ
11
ξ
1
+
γ
12
ξ
2
+
ζ
1
\eta_1=\beta_{12}\eta_2+\gamma_{11}\xi_1+\gamma_{12}\xi_2+\zeta_1
η1=β12η2+γ11ξ1+γ12ξ2+ζ1
η
2
=
γ
21
ξ
1
+
γ
22
ξ
2
+
ζ
2
\eta_2=\gamma_{21}\xi_1+\gamma_{22}\xi_2+\zeta_2
η2=γ21ξ1+γ22ξ2+ζ2 方程
Y
=
Λ
y
η
+
ϵ
Y=\Lambda_y\eta+\epsilon
Y=Λyη+ϵ可以表达为
(1.1.3-4)
[
y
1
y
2
y
3
y
4
]
=
[
1
0
λ
y
21
0
λ
y
31
0
0
λ
y
42
]
[
η
1
η
2
]
+
[
ϵ
1
ϵ
2
ϵ
3
ϵ
4
]
\left[ \begin{matrix} y_1\\ y_2\\ y_3\\ y_4 \end{matrix} \right]= \left[ \begin{matrix} 1 ; 0\\ \lambda_{y21} ; 0\\ \lambda_{y31} ; 0\\ 0 ; \lambda_{y42} \end{matrix} \right] \left[ \begin{matrix} \eta_1\\ \eta_2 \end{matrix} \right]+ \left[ \begin{matrix} \epsilon_1\\ \epsilon_2\\ \epsilon_3\\ \epsilon_4 \end{matrix} \right]\tag{1.1.3-4}
⎣⎢⎢⎡y1y2y3y4⎦⎥⎥⎤=⎣⎢⎢⎡1λy21λy310000λy42⎦⎥⎥⎤[η1η2]+⎣⎢⎢⎡ϵ1ϵ2ϵ3ϵ4⎦⎥⎥⎤(1.1.3-4)
Λ
y
\Lambda_y
Λy决定了那个具体的内生观察标识
y
y
y载荷在哪个具体内生潜变量
η
\eta
η上。固定值0标识某标识不载荷在相应的潜变量上。负载固定值1用于模型识别的需要,并定义潜变量的尺度。由1.1.3-4可以导出以下关于内生潜变量的测量方程:
y
1
=
η
1
+
ϵ
1
y_1=\eta_1+\epsilon_1
y1=η1+ϵ1
y
2
=
λ
y
21
η
1
+
ϵ
2
y_2=\lambda_{y21}\eta_1+\epsilon_2
y2=λy21η1+ϵ2
y
3
=
λ
y
31
η
1
+
ϵ
3
y_3=\lambda_{y31}\eta_1+\epsilon_3
y3=λy31η1+ϵ3
y
4
=
λ
y
42
η
2
+
ϵ
4
y_4=\lambda_{y42}\eta_2+\epsilon_4
y4=λy42η2+ϵ4 图1.1-1的模型中,方程
X
=
Λ
x
ξ
+
δ
X=\Lambda_x\xi+\delta
X=Λxξ+δ可以表达为:
结构方程模型的设定实际上是通过对这8个矩阵中的参数具体设定来表述的。这些参数可以设定为固定参数fixed parameter,也可以设定为自由参数free parameter。固定参数不能由数据估计,值通常固定为0(如协方差为零或斜率为零,表示无相关关系或效应),或1(如因模型识别的需要,通常,每个因子须有一个因子载荷设定为0)。 方程
η
=
B
η
+
Γ
ξ
+
ζ
\eta=B\eta+\Gamma\xi+\zeta
η=Bη+Γξ+ζ的矩阵表示为:
(1.1.3-2)
[
η
1
η
2
]
=
[
0
β
12
0
0
]
[
η
1
η
2
]
+
[
γ
11
γ
12
γ
21
γ
22
]
+
[
ζ
1
ζ
2
]
\left[ \begin{matrix} \eta_1 \\ \eta_2 \end{matrix} \right]=\left[ \begin{matrix} 0 ; \beta_{12}\\ 0 ; 0 \end{matrix} \right]\left[ \begin{matrix} \eta_1\\ \eta_2 \end{matrix} \right]+ \left[ \begin{matrix} \gamma_{11} ; \gamma_{12} \\ \gamma_{21} ; \gamma_{22} \end{matrix} \right]+ \left[ \begin{matrix} \zeta_1\\ \zeta_2 \end{matrix} \right]\tag{1.1.3-2}
[η1η2]=[00β120][η1η2]+[γ11γ21γ12γ22]+[ζ1ζ2](1.1.3-2) 图1.1-2所示模型可以导出以下两个结构方程
η
1
=
β
12
η
2
+
γ
11
ξ
1
+
γ
12
ξ
2
+
ζ
1
\eta_1=\beta_{12}\eta_2+\gamma_{11}\xi_1+\gamma_{12}\xi_2+\zeta_1
η1=β12η2+γ11ξ1+γ12ξ2+ζ1
η
2
=
γ
21
ξ
1
+
γ
22
ξ
2
+
ζ
2
\eta_2=\gamma_{21}\xi_1+\gamma_{22}\xi_2+\zeta_2
η2=γ21ξ1+γ22ξ2+ζ2 方程
Y
=
Λ
y
η
+
ϵ
Y=\Lambda_y\eta+\epsilon
Y=Λyη+ϵ可以表达为
(1.1.3-4)
[
y
1
y
2
y
3
y
4
]
=
[
1
0
λ
y
21
0
λ
y
31
0
0
λ
y
42
]
[
η
1
η
2
]
+
[
ϵ
1
ϵ
2
ϵ
3
ϵ
4
]
\left[ \begin{matrix} y_1\\ y_2\\ y_3\\ y_4 \end{matrix} \right]= \left[ \begin{matrix} 1 ; 0\\ \lambda_{y21} ; 0\\ \lambda_{y31} ; 0\\ 0 ; \lambda_{y42} \end{matrix} \right] \left[ \begin{matrix} \eta_1\\ \eta_2 \end{matrix} \right]+ \left[ \begin{matrix} \epsilon_1\\ \epsilon_2\\ \epsilon_3\\ \epsilon_4 \end{matrix} \right]\tag{1.1.3-4}
⎣⎢⎢⎡y1y2y3y4⎦⎥⎥⎤=⎣⎢⎢⎡1λy21λy310000λy42⎦⎥⎥⎤[η1η2]+⎣⎢⎢⎡ϵ1ϵ2ϵ3ϵ4⎦⎥⎥⎤(1.1.3-4)
Λ
y
\Lambda_y
Λy决定了那个具体的内生观察标识
y
y
y载荷在哪个具体内生潜变量
η
\eta
η上。固定值0标识某标识不载荷在相应的潜变量上。负载固定值1用于模型识别的需要,并定义潜变量的尺度。由1.1.3-4可以导出以下关于内生潜变量的测量方程:
y
1
=
η
1
+
ϵ
1
y_1=\eta_1+\epsilon_1
y1=η1+ϵ1
y
2
=
λ
y
21
η
1
+
ϵ
2
y_2=\lambda_{y21}\eta_1+\epsilon_2
y2=λy21η1+ϵ2
y
3
=
λ
y
31
η
1
+
ϵ
3
y_3=\lambda_{y31}\eta_1+\epsilon_3
y3=λy31η1+ϵ3
y
4
=
λ
y
42
η
2
+
ϵ
4
y_4=\lambda_{y42}\eta_2+\epsilon_4
y4=λy42η2+ϵ4 图1.1-1的模型中,方程
X
=
Λ
x
ξ
+
δ
X=\Lambda_x\xi+\delta
X=Λxξ+δ可以表达为: 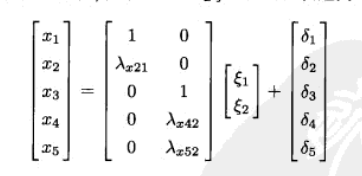
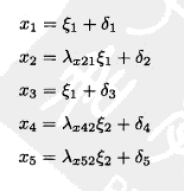 以上的测量模型和结构模型中,有如下假设:
E
(
ζ
)
=
0
,
E
(
ϵ
)
=
0
,
E
(
δ
)
=
0
E(\zeta)=0, E(\epsilon)=0, E(\delta)=0
E(ζ)=0,E(ϵ)=0,E(δ)=0以及
C
o
v
(
ζ
,
ξ
)
=
0
,
C
o
v
(
ϵ
,
η
)
=
0
,
C
o
v
(
δ
,
ξ
)
=
0
Cov(\zeta, \xi)=0, Cov(\epsilon, \eta)=0, Cov(\delta, \xi)=0
Cov(ζ,ξ)=0,Cov(ϵ,η)=0,Cov(δ,ξ)=0,还假设观察变量服从多元正态分布。
以上的测量模型和结构模型中,有如下假设:
E
(
ζ
)
=
0
,
E
(
ϵ
)
=
0
,
E
(
δ
)
=
0
E(\zeta)=0, E(\epsilon)=0, E(\delta)=0
E(ζ)=0,E(ϵ)=0,E(δ)=0以及
C
o
v
(
ζ
,
ξ
)
=
0
,
C
o
v
(
ϵ
,
η
)
=
0
,
C
o
v
(
δ
,
ξ
)
=
0
Cov(\zeta, \xi)=0, Cov(\epsilon, \eta)=0, Cov(\delta, \xi)=0
Cov(ζ,ξ)=0,Cov(ϵ,η)=0,Cov(δ,ξ)=0,还假设观察变量服从多元正态分布。