如何理解「梅涅劳斯定理」和「塞瓦定理」，这两个定理在实际中有什么应用？

张景中院士在《新概念几何》中利用「共边定理」证明「梅涅劳斯定理」和「塞瓦定理」，证明长度均为一行，而且引理本身也是足够简明直观，介绍如下：

该定理有四种情况，如下图：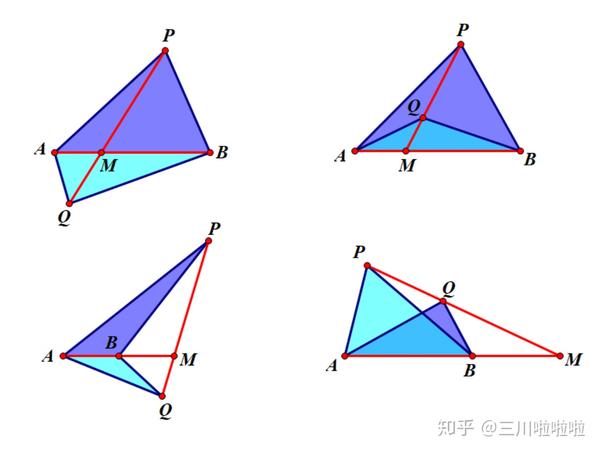

这个定理的证明就不用多说了吧！

接下来利用共边定理逐个击破：

三角形内三线交于一点，则有以下关系：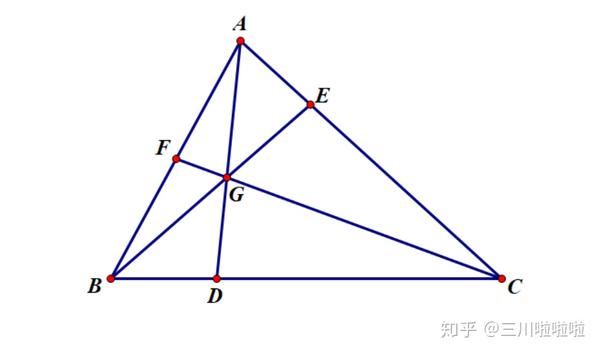

证明

（看好了，就一行）

Q. E. D

过三角形一边上的点做一直线，分别与其余两边或其延长线所截，则满足一下关系：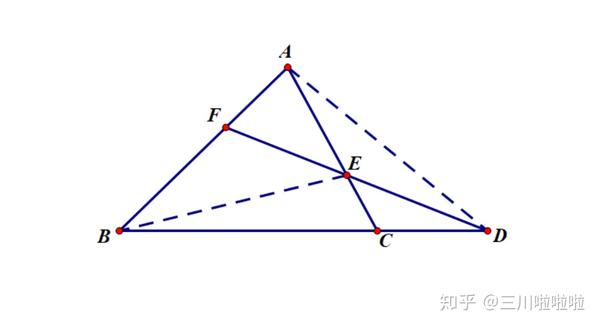

证明

（坐稳，开车了！）

Q. E. D

证明过程体现了两个定理的相似性。实际上这两个定理互为「对偶定理」，即只要证明其中一个，另一个自然成立。这是因为在射影平面中，确定一条直线和确定一个点，都需要三个坐标（齐次坐标），于是面空间与点空间形成了自然的同构，而这样的同构映射保持结合性不变，所谓结合性，就是指「点在线上」、「线过某点」这样的结合关系。

对偶图形包含两个方面：

它们俩的逆定理也是成立的，这根据三角形的唯一性可以得到。

在实际生活中，我能想到的是寻找据点发射炮弹。

就比如李云龙把一群小鬼子围在一个三角形区域，他打算从三个顶点向三角形内部的鬼子据点发射意大利炮，那么这个时候利用塞瓦定理，就可以减少测量次数，确定发射角度。历史上有人用「帕普斯定理」这样干的，所以就以此类推吧。

总之，在实际上生活中，如果遇到解三角形问题的时候，都可以考虑使用这两个定理，此处不再多讲。

在平面几何中，这两个定理的地位可以说举足轻重，应用广泛。

你从来没有对这些现象好奇过吗：

……

而这些情况，都可以收纳到塞瓦定理中，多么美妙！