| 数据分析基础 | 您所在的位置:网站首页 › 标准正态分布常用的三个分位数 › 数据分析基础 |
数据分析基础
|
学习资料:可汗学院公开课:统计学 1. 集中趋势与离散趋势通常一批数据,先看他们的描述统计(可画出箱型图),即看集中趋势和离散趋势。 集中趋势:集中趋势又称“数据的中心位置”、“集中量数”等。它是一组数据的代表值。统计学中常用平均数来描述一组变量值的集中位置或平均水平。常用的统计量指标有算数均数、几何均数、中位数和百分位数。 1)算数均数:即为均数,用以反映一组呈对称分布的变量值在数量上的平均水平。 2)几何均数:常用以反映一组经对数转换后呈对称分布的变量值在数量上的平均水平。 3)中位数:适用于偏态分布资料和一端或两端无确切的数值的资料。是第50百分位数 4)百分位数:为一界值,用以确定医学参考值范围。 离散趋势:离散趋势是反映数据的离散变异程度,常用指标有极差、四分位间距、方差与标准差、变异系数。 1)极差:为一组数据的最大值和最小值之差,但极差不能反映所有数据的变异大小,且极易受样本含量的影响。常用以描述偏态分布。 2)四分位数间距:它是由第3四分位数与第1四分位数相减得到,常和中位数一起描述偏态分布资料的分布。 3)方差与标准差:反映一组数据的平均离散水平,消除了样本含量的影响,常和均数一起用来描述一组数据中的离散和集中趋势。 4)变异系数:多用于观察指标单位不同时,可消除因单位不同而不能进行比较的困难。 总结:常用均数和标准差描述正态分布的集中和离散趋势;用中位数和四分位间距描述偏态分布的集中和离散趋势。 2. 总体方差(标准差)和样本方差(标准差)标准差主要是为了统一单位,更直观。例如方差的单位是
米
2
米^2
米2,标准差是米。 随机变量是表示随机现象各种结果的变量,可以认为是随机过程映射到数值的函数。随机变量是取值有多种可能并且取每个值都有一个概率的变量,它分为离散型和连续型两种,离散型随机变量的取值为有限个或者无限可列个(整数集是典型的无限可列),连续型随机变量的取值为无限不可列个(实数集是典型的无限不可列)。 离散型随机变量与概率分布描述离散型随机变量的概率分布的工具是概率分布表。 把分布表推广到无限情况,就可以得到连续型随机变量的概率密度函数。此时,随机变量取每个具体的值的概率为0,但在落在每一点处的概率是有相对大小的,描述这个概念的,就是概率密度函数。你可以把这个想象成一个实心物体,在每一点处质量为0,但是有密度,即有相对质量大小。 伯努利分布(Bernoulli distribution)又名两点分布或0-1分布,是最简单的二项分布。介绍伯努利分布前首先需要引入伯努利试验(Bernoulli trial)。 伯努利试验是只有两种可能结果的单次随机试验,即对于一个随机变量X而言: P(X=1) = p; P(X=0) = 1 - p; 均值E = p 方差V = p(1-p) 二项分布(Binomial distribution)二项分布是一种离散概率分布,表示在n次伯努利试验中,有k次成功的概率。 二项分布的命名是因为有成功和失败两项,泊松分布则是根据泊松这个人来命名的。它也是离散概率分布,与稀有事件的发生有关。 其实泊松分布就是二项分布的极限情况。当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。 5. 大数定理概念其实很简单,也就是样本数量足够多时,样本均值趋近于总体均值,或者说随机变量的期望值。 拿我们最熟悉的投色子举例,游戏规则是投中1点获得1元,投中2点获得2元,以此类推。 那么,这个事件的期望是多少呢? 显然是: 1 × 1 / 6 + 2 × 1 / 6 + 3 × 1 / 6 + 4 × 1 / 6 + 5 × 1 / 6 + 6 × 1 / 6 = 3.5 1\times 1/6+2\times 1/6+3\times 1/6+4\times 1/6+5\times 1/6+6\times 1/6=3.5 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6=3.5 这个期望3.5代表什么意思呢? 也就是说,只要你一直玩下去,你每次游戏的预期收益是3.5元。可能你某次赢了1元,某一次赢了6元,只要你长期投下去, 你平均下来每次就赢3.5元。 我们可以通过比较成本投入和期望收益,你就能知道这件事情值得不值得。 如果每玩1次需要缴纳5元,那么你玩1万次,你投入是5万元,那么你的收益将是3.5万元。显然不会有一个人玩1万次,但是长久下来,累积人数肯定有1万次,那么怎样都是商家收益。 6. 中心极限定理参考链接:中心极限定理 中心极限定理是说: 样本的平均值约等于总体的平均值。不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且样本平均值的分布呈正态分布。 中心极限定理和大数定律的区别(1)大数定律是说,n只要越来越大,把这n个独立同分布的数加起来去除以n得到的这个样本均值(也是一个随机变量)会依概率收敛到真值u,但是样本均值的分布是怎样的我们不知道。 (2)中心极限定理是说,n只要越来越大,这n个数的样本均值会趋近于正态分布,并且这个正态分布以u为均值,σ^2/n为方差。(就像上面所说,如果用样本估计总体标准方差则除以n-1) (3)综上所述,这两个定律都是在说样本均值性质。随着n增大,大数定律说样本均值几乎必然等于均值。中心极限定律说,它越来越趋近于正态分布,并且这个正态分布的方差越来越小。 直观上来讲,想到大数定律的时候,脑海里浮现的应该是一个样本,然后n就是该样本的数量,也就是样本数量足够多时,样本均值趋近于总体均值; 想到中心极限定理的时候脑海里应该浮现出总体中随机抽取了很多个样本(例如m个),然后n就是每个样本的样本大小(大小都一样的),求每个样本的均值,每一个总体的样本平均值都会围绕在总体的整体平均值周围。然后就有m个均值,该m个均值的分布趋近于均值为总体平均值μ,方差为 σ 2 / n σ^2/n σ2/n的正态分布(不管总体的分布是如何的),即随着样本容量n变大,抽样分布标准差越小,越收拢; 7. 正态分布
解:知道总体分布的均值和标准差,那么多次从总体抽取50个样本,其样本均值组成了均值为μ,方差为 σ 2 / n σ^2/n σ2/n的正态分布。 所以样本标准误差为 σ / s q r t ( n ) = 0.7 / s q r t ( 50 ) = 0.099 σ/sqrt(n) = 0.7/sqrt(50) = 0.099 σ/sqrt(n)=0.7/sqrt(50)=0.099,均值为50。110L水,平均每人喝2.2L,即求P(x>2.2)。由Z分数公式得(2.2-2)/0.099 = 2.02,就是计算在大于均值2.02个标准差的面积。查Z分数表知Z(2.02) = 0.9783(这个是小于2.02个标准差的面积),所以P(x>2.2) = 0.0217 从农场的200,000个苹果中抽样36个,该36个苹果均重112g,标准差为40。问这200,000个苹果的平均重量在100g到124g之间的概率是多少?解:该36个苹果均重112g,标准差为40,这个是样本标准差S并不是样本均值抽样分布的标准差,所以不能用 σ / s q r t ( n ) = 40 σ/sqrt(n)=40 σ/sqrt(n)=40来求总体标准差,而是应该直接样本标准差S来估计σ,这里直接约等于S,即40。 知道总体标准差就知道样本标准误差(样本均值抽样分布的标准差): 40 / s q r t ( n ) = 40 / 6 = 6.67 40/sqrt(n)=40/6=6.67 40/sqrt(n)=40/6=6.67,均值为112,Z值: ( 124 − 112 ) / 6.67 = 1.8 (124-112)/6.67=1.8 (124−112)/6.67=1.8,查表即可。 置信水平与置信区间如何通俗地解释置信水平与置信区间 从某学校抽取250教师,其中142人认为电脑是必备教学工具。 计算一个99%置信区间,其中教师认为电脑是必备工具。在保持99%的置信水平下,如何缩减置信区间? 总结步骤:求样本的平均值和标准误差确定置信水平,查Z表格,确定Z值确定置信区间的上下限 总结步骤:求样本的平均值和标准误差确定置信水平,查Z表格,确定Z值确定置信区间的上下限
通常来说,置信水平越高,置信区间越宽; 若保持置信水平,缩减置信区间,所以得通过减少标准误差,即增大样本数即可。 8.2 n组内均方,来自不同正态总体 ; 拒绝H0F |
【本文地址】
 很多书上都会把除以n-1的标准差叫做样本标准,其实会给很多人造成误解。其实这个样本标准差的目的是用于估计总体标准差。 你可能会疑惑,那我什么时候标准差除以n还是n-1呢?那就要看你使用标准差的目的是什么。
很多书上都会把除以n-1的标准差叫做样本标准,其实会给很多人造成误解。其实这个样本标准差的目的是用于估计总体标准差。 你可能会疑惑,那我什么时候标准差除以n还是n-1呢?那就要看你使用标准差的目的是什么。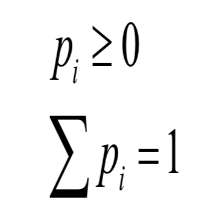



 最常见的连续型概率分布是正态分布,也称为高斯分布。它的概率密度函数为:
最常见的连续型概率分布是正态分布,也称为高斯分布。它的概率密度函数为: 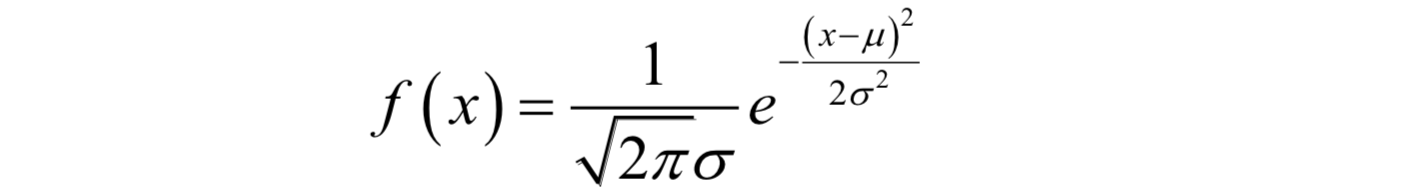 其中μ和
σ
2
σ^{2}
σ2分别为均值和方差。现实世界中的很多数据,例如人的身高、体重、寿命等都近似服从正态分布。 另外一种常用的分布是均匀分布,如果随机变量x服从区间[a,b]内的均匀分布,则其概率密度函数为:
其中μ和
σ
2
σ^{2}
σ2分别为均值和方差。现实世界中的很多数据,例如人的身高、体重、寿命等都近似服从正态分布。 另外一种常用的分布是均匀分布,如果随机变量x服从区间[a,b]内的均匀分布,则其概率密度函数为: 
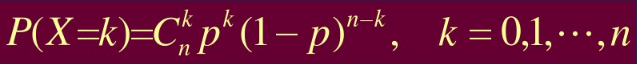 假设B1,B2,,,Bn为n次独立的伯努利试验,根据期望和方差的公式: 二项分布的期望为: E(B1 + B2 + … + Bn) = nE(B1) = np 方差: V(B1 + B2 + … + Bn) = nV(B1) = npq =np(1-p)
假设B1,B2,,,Bn为n次独立的伯努利试验,根据期望和方差的公式: 二项分布的期望为: E(B1 + B2 + … + Bn) = nE(B1) = np 方差: V(B1 + B2 + … + Bn) = nV(B1) = npq =np(1-p)

 z分数(z-score):
z分数(z-score): 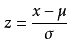 其中μ为总体平均值,X-μ为离均差,σ表示总体标准偏差。z分数是衡量数据点与均值之间相差了多少个标准差。并不是只有正态分布可以有计算z分数,任何分布都可以计算,只要有均值和标准差。
其中μ为总体平均值,X-μ为离均差,σ表示总体标准偏差。z分数是衡量数据点与均值之间相差了多少个标准差。并不是只有正态分布可以有计算z分数,任何分布都可以计算,只要有均值和标准差。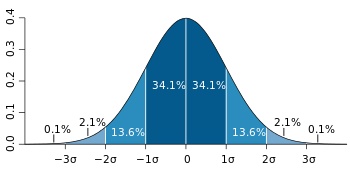 常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。
常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。


 在实际中,一家公司薪资的分布通常是右偏分布,而银行的风险风险分布是左偏分布(低风险)。
在实际中,一家公司薪资的分布通常是右偏分布,而银行的风险风险分布是左偏分布(低风险)。