| 动手学深度学习（二十四） | 您所在的位置：网站首页 › 标准化残差的计算公式 › 动手学深度学习（二十四） |
动手学深度学习（二十四）
|
一、为什么选择残差网络
在VGG中，卷积网络达到了19层，在GoogLeNet中，网络史无前例的达到了22层。那么，网络的精度会随着网络的层数增多而增多吗？在深度学习中，网络层数增多一般会伴着下面几个问题 计算资源的消耗（用GPU集群去怼）模型容易过拟合（扩大数据集、Droupout、批量归一化、正则化、初始化参数调整等等方法）梯度消失/梯度爆炸问题的产生（批量归一化）随着网络层数的增加，网络发生了退化（degradation）的现象：随着网络层数的增多，训练集loss逐渐下降，然后趋于饱和，当你再增加网络深度的话，训练集loss反而会增大。注意这并不是过拟合，因为在过拟合中训练loss是一直减小的。 当网络退化时，浅层网络能够达到比深层网络更好的训练效果，这时如果我们把低层的特征传到高层，那么效果应该至少不比浅层的网络效果差，或者说如果一个VGG-100网络在第98层使用的是和VGG-16第14层一模一样的特征，那么VGG-100的效果应该会和VGG-16的效果相同。所以，我们可以在VGG-100的98层和14层之间添加一条直接映射（Identity Mapping）来达到此效果。 从信息论的角度讲，由于DPI（数据处理不等式）的存在，在前向传输的过程中，随着层数的加深，Feature Map包含的图像信息会逐层减少，而ResNet的直接映射的加入，保证了 l + 1 l+1 l+1层的网络一定比 l l l层包含更多的图像信息。 基于这种使用直接映射来连接网络不同层直接的思想，残差网络应运而生。 二、残差网络（ResNet）随着我们设计越来越深的网络，深刻理解“新添加的层如何提升神经网络的性能”变得至关重要。更重要的是设计网络的能力，在这种网络中，添加层会使网络更具表现力，为了取得质的突破，我们需要一些数学基础知识。 2.1 函数类首先，假设有一类特定的神经网络结构 F \mathcal{F} F，它包括学习速率和其他超参数设置。对于所有 f ∈ F f \in \mathcal{F} f∈F，存在一些参数集（例如权重和偏置），这些参数可以通过在合适的数据集上进行训练而获得。 现在假设 f ∗ f^* f∗ 是我们真正想要找到的函数，如果是 f ∗ ∈ F f^* \in \mathcal{F} f∗∈F，那我们可以轻而易举的训练得到它，但通常我们不会那么幸运。相反，我们将尝试找到一个函数 f F ∗ f^*_\mathcal{F} fF∗，这是我们在 F \mathcal{F} F 中的最佳选择。例如，给定一个具有 X \mathbf{X} X 特性和 y \mathbf{y} y 标签的数据集，我们可以尝试通过解决以下优化问题来找到它： f F ∗ : = a r g m i n f L ( X , y , f ) subject to f ∈ F . (2.1) f^*_\mathcal{F} := \mathop{\mathrm{argmin}}_f L(\mathbf{X}, \mathbf{y}, f) \text{ subject to } f \in \mathcal{F}. \tag{2.1} fF∗:=argminfL(X,y,f) subject to f∈F.(2.1) 那么，怎样得到更近似真正 f ∗ f^* f∗ 的函数呢？ 唯一合理的可能性是，我们需要设计一个更强大的结构 F ′ \mathcal{F}' F′。换句话说，我们预计 f F ′ ∗ f^*_{\mathcal{F}'} fF′∗ 比 f F ∗ f^*_{\mathcal{F}} fF∗ “更近似”。然而，如果 F ⊈ F ′ \mathcal{F} \not\subseteq \mathcal{F}' F⊆F′，则无法保证新的体系“更近似”。 事实上， f F ′ ∗ f^*_{\mathcal{F}'} fF′∗ 可能更糟： 如下图所示，对于非嵌套函数（non-nested function）类，较复杂的函数类并不总是向“真”函数 f ∗ f^* f∗ 靠拢（复杂度由 F 1 \mathcal{F}_1 F1 向 F 6 \mathcal{F}_6 F6 递增）。在下图的左边，虽然 F 3 \mathcal{F}_3 F3 比 F 1 \mathcal{F}_1 F1 更接近 f ∗ f^* f∗，但 F 6 \mathcal{F}_6 F6 却离的更远了。相反对于图右侧的嵌套函数（nested function）类 F 1 ⊆ … ⊆ F 6 \mathcal{F}_1 \subseteq \ldots \subseteq \mathcal{F}_6 F1⊆…⊆F6，我们可以避免上述问题。 
因此，只有当较复杂的函数类包含较小的函数类时，我们才能确保提高它们的性能。对于深度神经网络，如果我们能将新添加的层训练成 恒等映射（identity function） f ( x ) = x f(\mathbf{x}) = \mathbf{x} f(x)=x ，新模型和原模型将同样有效。同时，由于新模型可能得出更优的解来拟合训练数据集，因此添加层似乎更容易降低训练误差。 针对这一问题，何恺明等人提出了残差网络（ResNet）He.Zhang.Ren.ea.2016。它在2015年的ImageNet图像识别挑战赛夺魁，并深刻影响了后来的深度神经网络的设计。残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一。于是，残差块 （residual blocks） 便诞生了，这个设计对如何建立深层神经网络产生了深远的影响。凭借它，ResNet 赢得了 2015 年 ImageNet 大规模视觉识别挑战赛。 2.2 残差块让我们聚焦于神经网络局部：如下图所示，假设我们的原始输入为 x x x ，而希望学出的理想映射为 f ( x ) f(\mathbf{x}) f(x) （作为 residual_block 上方激活函数的输入）。下左图虚线框中的部分需要直接拟合出该映射 f ( x ) f(\mathbf{x}) f(x) ，而右图虚线框中的部分则需要拟合出残差映射 f ( x ) − x f(\mathbf{x}) - \mathbf{x} f(x)−x 。 残差映射在现实中往往更容易优化。以上一节中提到的恒等映射作为我们希望学出的理想映射 f ( x ) f(\mathbf{x}) f(x) ，我们只需将 residual_block 中右图虚线框内上方的加权运算（如仿射）的权重和偏置参数设成 0，那么 f ( x ) f(\mathbf{x}) f(x) 即为恒等映射。 实际中，当理想映射 f ( x ) f(\mathbf{x}) f(x) 极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。residual_block 右图是 ResNet 的基础结构-- 残差块（residual block）。在残差块中，输入可通过跨层数据线路更快地向前传播。 这里可能会让人有一些混淆，梳理一下： 网络的每一层我们看作是： y = H ( x ) y = H(x) y=H(x),也就是这里的输出 f ( x ) f(x) f(x)残差网络的一个残差块可以表示为： H ( x ) = F ( x ) + x H(x) = F(x) + x H(x)=F(x)+x,这里的 F ( x ) F(x) F(x)等价于residual_block 右图虚线框中的部分那么就可以得到： F ( x ) = H ( x ) − x F(x) = H(x) -x F(x)=H(x)−x,也就是 f ( x ) − x f(x) - x f(x)−x
残差块的结构： ResNet 沿用了 VGG 完整的 3 × 3 3\times 3 3×3 卷积层设计。残差块里首先有 2 个有相同输出通道数的 3 × 3 3\times 3 3×3 卷积层。每个卷积层后接一个批量归一化层和 ReLU 激活函数。然后我们通过跨层数据通路，跳过这 2 个卷积运算，将输入直接加在最后的 ReLU 激活函数前。这样的设计要求 2 个卷积层的输出与输入形状一样，从而可以相加。如果想改变通道数，就需要引入一个额外的 1 × 1 1\times 1 1×1 卷积层来将输入变换成需要的形状后再做相加运算。 2.3 残差网络的数学原理参差网络的通用表示方式是： y l = h ( x l ) + F ( x l , W l ) (2.2) y_l = h(x_l)+ F(x_l,W_l) \tag{2.2} yl=h(xl)+F(xl,Wl)(2.2) x l + 1 = f ( y l ) (2.3) x_{l+1} = f(y_l) \tag{2.3} xl+1=f(yl)(2.3) 现在我们先不考虑升维或者降维的情况，那么假设公式2.2和2.3中 h ( . ) h(.) h(.)是直接映射 f ( . ) f(.) f(.)是激活函数，一般使用ReLU。那么残差块儿可表示为： x l + 1 = x l + F ( x l , W l ) (2.4) x_{l+1} = x_l + F(x_l,W_l) \tag{2.4} xl+1=xl+F(xl,Wl)(2.4) 对于一个更深的层L，其与l层的关系可以表示为： x L = x l + ∑ i = l L − 1 F ( x i , W i ) (2.5) x_L = x_l + \sum_{i=l}^{L-1}F(x_i,W_i) \tag{2.5} xL=xl+i=l∑L−1F(xi,Wi)(2.5) 公式2.5 反映残差网络的两个特性： L层可以用任意一个比它浅的l层网络和他们之间的残差部分之和进行表示公式中L是各个残差块特征的单位累和，而MLP是特征矩阵累积根据向后传播中使用的导数的链式法则，损失函数 ϵ \epsilon ϵ关于 x l x_l xl的梯度可以表示为： ∂ ϵ ∂ x l = ∂ ϵ ∂ x L ∂ x L ∂ x l = ∂ ϵ ∂ x L ( 1 + ∂ ∂ x l ∑ i = l L − 1 F ( x i , W i ) ) = ∂ ϵ ∂ x L + ∂ ϵ ∂ x L ∂ ∂ x l ∑ i = l L − 1 F ( x i , W i ) (2.6) \begin{aligned} \frac{\partial{\epsilon}}{\partial{x_l}} &= \frac{\partial{\epsilon}}{\partial{x_L}}\frac{\partial{x_L}}{\partial{x_l}} \\ &= \frac{\partial{\epsilon}}{\partial{x_L}}(1+\frac{\partial{}}{\partial{x_l}}\sum_{i=l}^{L-1}F(x_i,W_i))\\ &= \frac{\partial{\epsilon}}{\partial{x_L}}+ \frac{\partial{\epsilon}}{\partial{x_L}}\frac{\partial{}}{\partial{x_l}}\sum_{i=l}^{L-1}F(x_i,W_i)\\ \end{aligned} \tag{2.6} ∂xl∂ϵ=∂xL∂ϵ∂xl∂xL=∂xL∂ϵ(1+∂xl∂i=l∑L−1F(xi,Wi))=∂xL∂ϵ+∂xL∂ϵ∂xl∂i=l∑L−1F(xi,Wi)(2.6) 公式2.6 中反映了： 在整个训练过程中， ∂ x l ∑ i = l L − 1 F ( x i , W i ) {\partial{x_l}}\sum_{i=l}^{L-1}F(x_i,W_i) ∂xl∑i=lL−1F(xi,Wi)不可能一直为-1，所以残差网络中不会出现梯度消失的问题 ∂ ϵ ∂ x l \frac{\partial{\epsilon}}{\partial{x_l}} ∂xl∂ϵ表示L层的梯度可以直接传递给任何一个比其浅的l层 2.4 直接映射是最好选择？1.3 中我们假设了 h ( . ) h(.) h(.)是直接映射 f ( . ) f(.) f(.)是激活函数，一般使用ReLU。对于假设1，采用反证法：假设 h ( x l ) = λ l x l h(x_l) = \lambda_{l}x_l h(xl)=λlxl,那么这个时候残差块可以表示为： x l + 1 = λ l x l + F ( x l , W l ) (2.7) x_{l+1} = \lambda_lx_l+F(x_l,W_l) \tag{2.7} xl+1=λlxl+F(xl,Wl)(2.7) 对于更深的层： x L = ( ∏ i = l L − 1 λ i ) x l + ∑ i = l L − 1 F ( x i , W i ) (2.8) x_L = (\prod_{i=l}^{L-1}\lambda_i)x_l + \sum_{i=l}^{L-1}F(x_i,W_i) \tag{2.8} xL=(i=l∏L−1λi)xl+i=l∑L−1F(xi,Wi)(2.8) 为了简化问题，只考虑公式左半部分 x L = ( ∏ i = l L − 1 λ i ) x l x_L = (\prod_{i=l}^{L-1}\lambda_i)x_l xL=(∏i=lL−1λi)xl,损失函数 ϵ \epsilon ϵ关于 x l x_l xl的梯度可以表示为： ∂ ϵ ∂ x l = ∂ ϵ ∂ x L ( ( ∏ i = l L − 1 λ i ) + ∂ ∂ x l F ( x i , W i ) ) (2.9) \frac{\partial{\epsilon}}{\partial{x_l}} = \frac{\partial{\epsilon}}{\partial{x_L}}((\prod_{i=l}^{L-1}\lambda_i)+\frac{\partial{}}{\partial{x_l}}F(xi,Wi)) \tag{2.9} ∂xl∂ϵ=∂xL∂ϵ((i=l∏L−1λi)+∂xl∂F(xi,Wi))(2.9) 这个公式反映了： 当 λ > 1 \lambda > 1 λ>1，很有可能发生梯度爆炸（因为是连乘）当 λ < 1 \lambda < 1 λtrain_acc:.3f}, ' f'test acc {test_acc:.3f}') print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec ' f'on {str(device)}') lr, num_epochs, batch_size = 0.05, 10, 256 train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=96) train(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu()) loss 0.019, train acc 0.994, test acc 0.882 854.6 examples/sec on cuda:0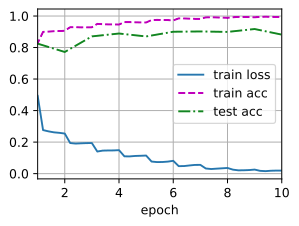
四、总结及问题
4.1 总结
学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。残差网络（ResNet）对随后的深层神经网络设计产生了深远影响，无论是卷积类网络还是全连接类网络。
4.2 问题
Inception块与残差块之间的主要区别是什么？在删除了Inception块中的一些路径之后，它们是如何相互关联的？
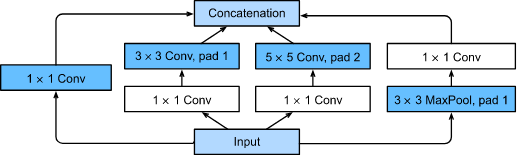
参考 ResNet 论文He.Zhang.Ren.ea.2016 中的表 1，以实现不同的变体。
参考文章详解残差网络 对于更深层次的网络，ResNet 引入了“bottleneck”架构来降低模型复杂性。请你试着去实现它。之后再实现 在 ResNet 的后续版本中，作者将“卷积层、批量归一化层和激活层”结构更改为“批量归一化层、激活层和卷积层”结构。请你做这个改进。详见 He.Zhang.Ren.ea.2016*1 中的图 1。调整一下结构即可，效果还不错 为什么即使函数类是嵌套的，我们仍然要限制增加函数的复杂性呢？我认为第一是因为复杂的函数会增加拟合的计算要求，第二是增加了过拟合的风险，第三是复杂的函数对网络结构底层训练的要求太大，实现起来效果会很差 |
【本文地址】