| 【精选】从crc32到linux内核实现 | 您所在的位置:网站首页 › 查表法crc32 › 【精选】从crc32到linux内核实现 |
【精选】从crc32到linux内核实现
|
0. 序
本文主要讨论软件方法计算crc32的算法以及linux内核中的实现。 1. 基本概念crc32主要用于通信中的数据完整性校验。基于网上已经有一大堆相关的阐述,这里就不再赘述。不过还是回顾一下基本的计算方法。 通信双方需要约定一个基本的作为除数的多项式,且在mod2的意义下考虑多项式的系数(因此系数只能是0或1)。将待传输的数据视为多项式的系数(每个bit对应一个系数),使其作为被除数。这里需要严格定义一下如何把一组数据映射到多项式的系数上:一组数据可以用一个指针地址加一个byte长度表示。地址越低,对应的多项式系数越高(主要方便接收方校验)。而对于一个byte内部,如果约定是most significant bit对应多项式的高次系数,这称为正向校验,如果是least significant bit作为多项式的高次系数,这称为反向校验。 举一个两字节数据的例子 低地址 -> 高地址 {0x12, 0x34 } // 二进制:00010010b, 00110100b如果是正向校验,这组数据映射到的多项式为 x 12 + x 9 + x 5 + x 4 + x 2 x^{12}+x^9+x^5+x^4+x^2 x12+x9+x5+x4+x2 而如果是反向校验,则映射为 x 14 + x 11 + x 5 + x 3 + x 2 x^{14}+x^{11}+x^5+x^3+x^2 x14+x11+x5+x3+x2 这样的话,由于crc校验位都是最后发送的(即位于高地址处),若设事先约定的除数多项式为 R ( x ) R(x) R(x),数据对应的多项式为 P ( x ) P(x) P(x),而crc校验位对应的多项式为 Q ( x ) Q(x) Q(x),且 Q ( x ) Q(x) Q(x)的次数为 α − 1 \alpha-1 α−1,那么在接收方看到的多项式则为 P ( x ) x α + Q ( x ) P(x)x^\alpha+Q(x) P(x)xα+Q(x),我们希望选取适当的 Q ( x ) Q(x) Q(x),使得 R ( x ) ∣ P ( x ) x α + Q ( x ) ( m o d 2 ) R(x)\quad |\quad P(x)x^\alpha+Q(x)(\bmod 2) R(x)∣P(x)xα+Q(x)(mod2) 由多项式带余除法的知识可以知道,若 R ( x ) R(x) R(x)的次数为 α \alpha α,则我们可以唯一地选取一个次数不超过 α − 1 \alpha-1 α−1的多项式 Q ( x ) Q(x) Q(x),使得 R ( x ) ∣ P ( x ) x α − Q ( x ) ≡ P ( x ) x α + Q ( x ) ( m o d 2 ) R(x)\quad |\quad P(x)x^\alpha-Q(x)\equiv P(x)x^\alpha+Q(x) (\bmod 2) R(x)∣P(x)xα−Q(x)≡P(x)xα+Q(x)(mod2) 现在对于crc32来说, R ( x ) R(x) R(x)是一个如下的次数为32的多项式(一般地,crcN的除数多项式次数为N) x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x 1 + 1 x^{32}+x^{26}+x^{23}+x^{22}+x^{16}+x^{12}+x^{11}+x^{10}+x^8+x^7+x^5+x^4+x^2+x^1+1 x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x1+1因此我们需要在数据末尾额外添加32bit的crc校验位,代表一个次数不超过31的多项式 Q ( x ) Q(x) Q(x),且为得到 Q ( x ) Q(x) Q(x)只需要做一个带余除法就好 Q ( x ) ≡ P ( x ) x 32 ( m o d 2 ) Q(x) \equiv P(x)x^{32} (\bmod 2) Q(x)≡P(x)x32(mod2) 2. linux内核对1bit算法的实现为求一组数据的crc,最简单的算法就是模拟多项式带余除法的过程,每次循环移位1bit(好图出处)。 Linux内核实现位于lib/crc32.c文件中。正向校验的实现如下 static inline u32 __pure crc32_be_generic(u32 crc, unsigned char const *p, size_t len, const u32 (*tab)[256], u32 polynomial) { #if CRC_BE_BITS == 1 // 表示采用 1bit算法 int i; while (len--) { crc ^= *p++ crc ^= *p++; // 余数修正 for (i = 0; i > 1) ^ ((crc & 1) ? polynomial : 0); } return crc; }反向校验时一个byte的LSB对应多项式的高次系数,为了方便移位,此时crc的第k位bit对应多项式的 x 31 − k x^{31-k} x31−k项的系数,根据这个对应关系,不难知道传入的polynomial参数的值应为0xEDB88320。 上面的正向校验或者反向校验的代码并不依赖于大小端(因为数据是逐byte读入的)。但从linux的函数命名中可以看出前者更与大端绑定,后者更与小端绑定。能想到的一种猜测是,对于正向校验而言,如果是小端机器,crc的most significant byte是在高地址,而这个byte对应的是多项式的高次。因此在把crc值copy到数据末尾时,需要提前先把crc转为大端,使得多项式的高次在低地址处。而大端机器就省略了这一步。反向校验也是同样的分析。 在之前为了便于理解,我们假定了传入的crc初始参数为0,不过在真实情况下一般初始值为0xffffffff。在内核文档中有如下解释 Two more details about CRC implementation in the real world: Normally, appending zero bits to a message which is already a multiple of a polynomial produces a larger multiple of that polynomial. Thus, a basic CRC will not detect appended zero bits (or bytes). To enable a CRC to detect this condition, it’s common to invert the CRC before appending it. This makes the remainder of the message+crc come out not as zero, but some fixed non-zero value. (The CRC of the inversion pattern, 0xffffffff.) The same problem applies to zero bits prepended to the message, and a similar solution is used. Instead of starting the CRC computation with a remainder of 0, an initial remainder of all ones is used. As long as you start the same way on decoding, it doesn’t make a difference. 也就是说,传入初始crc非0是为了检测传输过程中多余的前导0。另外,为了检测传输过程中末尾的多余0,crc值通常会bit反转。最终的data + crc对应的多项式就不再是除数多项式的倍数了,这样接收方校验出的crc不再是0,而是0xffffffff的crc值。 3 Sarwate algorithm1988年,Dilip V. Sarwate 在论文Computation of Cyclic Redundancy Checks via Table Look-Up中提出了使用lookup table来加速crc计算的方法。这样每次循环内部可以处理一个byte的数据。原论文对于lookup table的构造写得复杂了,其实lookup table要存的就是提前算好的多项式余数嘛。 对于计算crc32, 一般地,我们假设希望一次处理N bit的数据,那么需要准备一个u32 table[1 # elif CRC_LE_BITS == 8 // 表示使用 Sarwate algorithm算法 /* aka Sarwate algorithm */ while (len--) { crc ^= *p++; // 余数修正 crc = (crc >> 8) ^ tab[0][crc & 255]; } // tab[0]对应的是上面提到的256个表项的table return crc; } /* 一个更加原始的版本,请忽略可能的大小端问题以及数组越界的问题 while(len--){ u32 tmp = tab[0][*p++]; *(u32*)p ^= tmp; } return *p; */ 额外解释一下算法是怎么进行的:Sarwate在论文中提到,如果按照原本的查表法,我们不得不修改原本的字符序列(参考上面的更加原始的版本),这里用到的trick是,我们把tab表中对接下来的byte的余数影响存到了crc这个临时变量里(或者理解为我们假设接下来的byte都是0),到实际需要访问表项时再读入接下来的byte,通过摸2加法求出真实的余数,再用这个结果去访问表项(所谓的余数修正,类似的trick在1bit算法中也用到了)。 另外值得注意的是,该算法的实现也不依赖于端序。 4. slice-by-N algorithm(端序)读者很容易把上面描述的Sarwate algorithm推广到一次处理16bit甚至更多,但此时table表项指数级增加是不能够接受的。在05年时,Intel提出了slice-by-N algorithm,号称能够一次处理任意多的bit,而且table表项的大小是线性增加的(但实际并没有这么神,所以我用了号称这个词)。 具体想法是这样,以一次处理32bit为例(论文中称为slice-by-4),我们需要一个u32 table[4][256],table[0]就对应Sarwate algorithm中的256表项,即 t a b l e [ 0 ] [ I ] table[0][I] table[0][I]为 I I I的crc余数,一般地, t a b l e [ k ] [ I ] table[k][I] table[k][I]存放的是 I ∗ 2 8 k I*2^{8k} I∗28k的crc余数。对应一个32bit数M,M的crc余数可以由如下式子给出(只是直观的结果,忽略了正反校验以及端序的影响) table[0][M & 255] ^ table[1][(M >> 8) & 255] ^ table[2][(M >> 16) & 255] ^ table[3][(M >> 24) & 255]可以看到,虽然说一次处理32bit,但其实查表次数和原本的Sarwate algorithm是一样的,不过从原论文中可以看出,算术运算次数确实减少了,以及访问待计算crc的byte序列的次数确实减少了。另外,把算法应用到一次处理64bit,可以发现一个额外的bonus:读取的64bit中,有32bit不需要进行余数修正(因为每次算出的余数只有32bit)。 现在我们来看看内核的实现,值得注意的是,因为一次处理不止一个byte,我们需要注意端序给代码带来的影响。选取的代码是正向校验,且实现slice-by-8。 static inline u32 __pure crc32_be_generic(u32 crc, unsigned char const *p, size_t len, const u32 (*tab)[256], u32 polynomial){ crc = (__force u32) __cpu_to_be32(crc); // 把crc转为大端表示 crc = crc32_body(crc, p, len, tab); crc = __be32_to_cpu((__force __be32)crc); // 将结果crc从大端转回cpu端序 return crc; }我们看到,在调用实际计算crc32的代码前,先进行了一个端序转换,再一次提醒读者,在正向校验时,tab中存的32位bit依次对应余数多项式的32个系数(第31位bit对应多项式的第31次方系数,以此类推)。而linux传入的tab实际上也进行了一个端序转换,在crc32table.h文件中,正向校验的table表声明如下 static const u32 ____cacheline_aligned crc32table_be[8][256] = {{ tobe(0x00000000L), tobe(0x04c11db7L), tobe(0x09823b6eL), tobe(0x0d4326d9L), tobe(0x130476dcL), tobe(0x17c56b6bL), tobe(0x1a864db2L), tobe(0x1e475005L), tobe(0x2608edb8L), tobe(0x22c9f00fL), tobe(0x2f8ad6d6L), tobe(0x2b4bcb61L), tobe(0x350c9b64L), tobe(0x31cd86d3L), tobe(0x3c8ea00aL), tobe(0x384fbdbdL), ...... } }tobe宏的声明来自crc32.c #if CRC_BE_BITS > 8 // 表示使用slice-by-N算法 # define tobe(x) ((__force u32) cpu_to_be32(x)) #else // 表示使用Sarwate algorithm或者1bit算法 # define tobe(x) (x) #endif前面提到过,1bit算法以及Sarwate algorithm并不依赖于端序,因此tobe是一个空操作,而在slice-by-N算法中,把余数表转为了大端序,我们在接下来分析crc32_body函数时将会看到这样做的原因。 下面的代码剔除了一些无关的预编译判断。为了便于分析,不妨假设是一台小端机器。 static inline u32 __pure crc32_body(u32 crc, unsigned char const *buf, size_t len, const u32 (*tab)[256]) { # ifdef __LITTLE_ENDIAN # define DO_CRC(x) crc = t0[(crc ^ (x)) & 255] ^ (crc >> 8) # define DO_CRC4 (t3[(q) & 255] ^ t2[(q >> 8) & 255] ^ \ t1[(q >> 16) & 255] ^ t0[(q >> 24) & 255]) # define DO_CRC8 (t7[(q) & 255] ^ t6[(q >> 8) & 255] ^ \ t5[(q >> 16) & 255] ^ t4[(q >> 24) & 255]) # else # define DO_CRC(x) crc = t0[((crc >> 24) ^ (x)) & 255] ^ (crc 8) & 255] ^ \ t2[(q >> 16) & 255] ^ t3[(q >> 24) & 255]) # define DO_CRC8 (t4[(q) & 255] ^ t5[(q >> 8) & 255] ^ \ t6[(q >> 16) & 255] ^ t7[(q >> 24) & 255]) # endif const u32 *b; size_t rem_len; const u32 *t0=tab[0], *t1=tab[1], *t2=tab[2], *t3=tab[3]; const u32 *t4 = tab[4], *t5 = tab[5], *t6 = tab[6], *t7 = tab[7]; u32 q; /* Align it */ if (unlikely((long)buf & 3 && len)) { do { DO_CRC(*buf++); } while ((--len) && ((long)buf)&3); } rem_len = len & 7; len = len >> 3; b = (const u32 *)buf; for (--b; len; --len) { q = crc ^ *++b; /* use pre increment for speed */ crc = DO_CRC8; q = *++b; // bonus:这里不需要进行余数修正,少一次异或运算 crc ^= DO_CRC4; } len = rem_len; /* And the last few bytes */ if (len) { u8 *p = (u8 *)(b + 1) - 1; do { DO_CRC(*++p); /* use pre increment for speed */ } while (--len); } return crc; #undef DO_CRC #undef DO_CRC4 #undef DO_CRC8 }函数的第一步是对buf进行四字节的对齐,如果没有对齐,就反复调用Sarwate algorithm,直到buf对齐为止。如果原本机器是小端,由于这里crc和tab都是大端序,因此余数多项式的高次项系数被反转到了低位byte上,所以DO_CRC中拿到差别系数的方法是crc ^ (x)) & 255,即拿出余数的最低位。而如果原本机器是大端,因此crc和tab都没有被反转,余数多项式的高次项系数仍然在高位byte,所以DO_CRC中是用余数的最高位byte来查表(可以看到,这与原本的算法正好反过来了)。 对齐buf之后就是进行slice-by-8的算法了。重点是要想明白从byte序列中读一个u32后,该u32的bit如何对应到多项式的系数上。假设是小端机器,读一个u32后,原本byte序列的低地址对应余数多项式的高次系数,同时低地址又对应到u32的低位。因此这个u32的高位byte对应余数多项式的低位系数,但原本计算出的正向校验的tab是高位byte对应余数多项式的高位系数,因此我们把tab和原始的crc都转为大端序,这样便和读入的u32对齐了(对于大端机器分析,可以发现读入的u32是自然和原本的tab对齐的)。这便是转为大端序的本质原因。 考虑到最后如果buf的长度不是8字节对齐的,该函数最后又调用Sarwate algorithm把非对齐的byte解决掉,然后返回最后的结果。 另外,上面转为大端序是基于计算正向校验的前提,根据对称性可以猜测,如果是计算反向校验,那么应该转为小端序(事实的确如此)。 5. 结本文主要参考了Computation of Cyclic Redundancy Checks via Table Look-Up以及slice-by-N algorithm这两篇论文。算法本身并不难,不过看真实算法的代码时,考虑到各种细节还是挺绕的(尤其是端序的问题)。 另外,在思考有关端序的问题上,LSB, MSB这样的概念是有效的抽象(可以隔离掉端序的干扰)。 |
【本文地址】
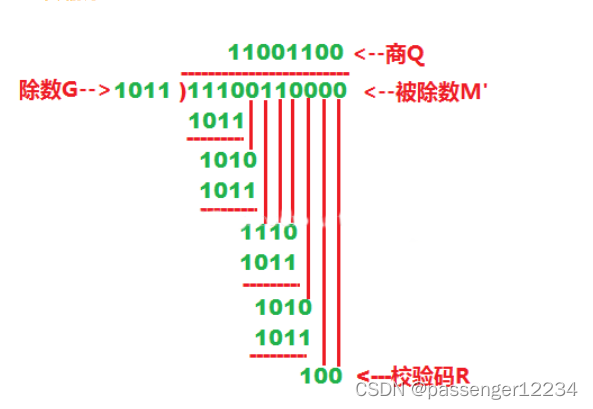 运算过程中每次看目前的余数多项式的最高位,如果是1,则减去一个除数多项式,然后除数右移,如果是0,单纯除数右移。
运算过程中每次看目前的余数多项式的最高位,如果是1,则减去一个除数多项式,然后除数右移,如果是0,单纯除数右移。