| 【《机器人技术》复习】 | 您所在的位置:网站首页 › 机械手简图自由度的计算例题解析 › 【《机器人技术》复习】 |
【《机器人技术》复习】
|
【《机器人技术》复习】
1. 要求:2. 机械手运动解算问题2.1 自由度考点2.2 运动学方程2.3 动力学方程2.4 传感器2.5 编程题
1. 要求:
本次大作业上交截止时间 之前,超时,本门课程判定不及格。 作业上交的格式如下
一律以 WORD 文档的形式上交,如需提交图片,将图片插入 WORD 中,不可单独提交图片文件。命名格式为:姓名+学号+机器人技术大作业 20 春,例:张三+学号+ 机器人技术大作业。请各位同学一定注意格式,格式不正确的不予计分。
要求独立完成,不允许出现雷同卷,出现雷同的作业全部判定不及格。题目:
2. 机械手运动解算问题
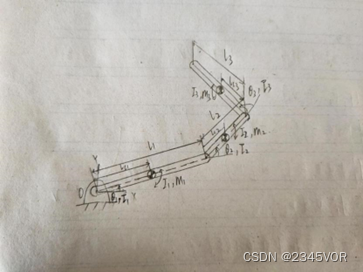
下图所示为某一机械手简图,试完成下列问题: 在设计图示机械手时,如何选择自由度?图示机械手自由度是多少? (5 分) 解:由图可机械手只需要在xoy平面内运动,平面二维空间运动最少需要2个,最多只需要3个自由度;图示机械手自由度是3个。 2.2 运动学方程请用 D-H 方法建立图示机械手各附体坐标系。 (5 分) 列出图示中连杆的 D-H 参数表。 (5 分) |连杆| α i \alpha_i αi| a i a_i ai | d i d_i di | θ i \theta_i θi| |-- |-- |-- |-- |-- | |1 |0 | l 1 l_1 l1| 0 | θ 1 \theta_1 θ1| |2 |0 | l 2 l_2 l2| 0 | θ 2 \theta_2 θ2| |3 |0 | l 3 l_3 l3| 0| θ 3 \theta_3 θ3| 表 1D-H 参数表 建立图示机械手的运动学方程。 (15 分) 该3自由度机械手的变换矩阵: 0 T 3 = A 1 A 2 A 3 {{^0}T}_3=A_1A_2A_3 0T3=A1A2A3; A 1 = [ c θ 1 − s θ 1 l 1 c θ 1 s θ 1 c θ 1 l 1 s θ 1 0 0 1 ] A_1=\left[\begin{matrix}c\theta_1&-s\theta_1&l_1c\theta_1\\s\theta_1&c\theta_1&l_1s\theta_1\\0&0&1\\\end{matrix}\right] A1=⎣⎡cθ1sθ10−sθ1cθ10l1cθ1l1sθ11⎦⎤ ; A 2 = [ c θ 2 − s θ 2 l 2 c θ 2 s θ 2 c θ 2 l 2 s θ 2 0 0 1 ] A_2=\left[\begin{matrix}c\theta_2&-s\theta_2&l_2c\theta_2\\s\theta_2&c\theta_2&l_2s\theta_2\\0&0&1\\\end{matrix}\right] A2=⎣⎡cθ2sθ20−sθ2cθ20l2cθ2l2sθ21⎦⎤ ; A 3 = [ c θ 3 − s θ 3 l 3 c θ 3 s θ 3 c θ 3 l 3 s θ 3 0 0 1 ] A_3=\left[\begin{matrix}c\theta_3&-s\theta_3&l_3c\theta_3\\s\theta_3&c\theta_3&l_3s\theta_3\\0&0&1\\\end{matrix}\right] A3=⎣⎡cθ3sθ30−sθ3cθ30l3cθ3l3sθ31⎦⎤ ; 0 T 3 = [ c θ 123 − s θ 123 l 1 c θ 1 + l 2 c θ 12 + l 3 c θ 123 s θ 123 c θ 123 l 1 s θ 1 + l 2 s θ 12 + l 3 s θ 123 0 0 1 ] {{^0}T}_3=\left[\begin{matrix}c\theta_{123}&-s\theta_{123}&l_1c\theta_1+l_2c\theta_{12}+l_3c\theta_{123}\\s\theta_{123}&c\theta_{123}&l_1s\theta_1+l_2s\theta_{12}+l_3s\theta_{123}\\0&0&1\\\end{matrix}\right] 0T3=⎣⎡cθ123sθ1230−sθ123cθ1230l1cθ1+l2cθ12+l3cθ123l1sθ1+l2sθ12+l3sθ1231⎦⎤ 2.3 动力学方程建立图示机械手的雅克比矩阵。 (15 分) J L 1 = b 0 × r 0 , e = ∣ i j k 0 0 1 l 1 c θ 1 + l 2 c θ 12 + l 3 c θ 123 l 1 s θ 1 + l 2 s θ 12 + l 3 s θ 123 0 ∣ = [ − l 1 s θ 1 − l 2 s θ 12 − l 3 s θ 123 l 1 c θ 1 + l 2 c θ 12 + l 3 c θ 123 0 ] J_{L1}=b_0\times r_{0,e}=\left|\begin{matrix}i&j&k\\0&0&1\\l_1c\theta_1+l_2c\theta_{12}+l_3c\theta_{123}&l_1s\theta_1+l_2s\theta_{12}+l_3s\theta_{123}&0\\\end{matrix}\right|=\left[\begin{matrix}-l_1s\theta_1-l_2s\theta_{12}-l_3s\theta_{123}\\l_1c\theta_1+l_2c\theta_{12}+l_3c\theta_{123}\\0\\\end{matrix}\right] JL1=b0×r0,e=∣∣∣∣∣∣i0l1cθ1+l2cθ12+l3cθ123j0l1sθ1+l2sθ12+l3sθ123k10∣∣∣∣∣∣=⎣⎡−l1sθ1−l2sθ12−l3sθ123l1cθ1+l2cθ12+l3cθ1230⎦⎤ J L 2 = b 1 × r 1 , e = ∣ i j k 0 0 1 l 2 c θ 12 + l 3 c θ 123 l 2 s θ 12 + l 3 s θ 123 0 ∣ = [ − l 2 s θ 12 − l 3 s θ 123 l 2 c θ 12 + l 3 c θ 123 0 ] J_{L2}=b_1\times r_{1,e}=\left|\begin{matrix}i&j&k\\0&0&1\\l_2c\theta_{12}+l_3c\theta_{123}&l_2s\theta_{12}+l_3s\theta_{123}&0\\\end{matrix}\right|=\left[\begin{matrix}-l_2s\theta_{12}-l_3s\theta_{123}\\l_2c\theta_{12}+l_3c\theta_{123}\\0\\\end{matrix}\right] JL2=b1×r1,e=∣∣∣∣∣∣i0l2cθ12+l3cθ123j0l2sθ12+l3sθ123k10∣∣∣∣∣∣=⎣⎡−l2sθ12−l3sθ123l2cθ12+l3cθ1230⎦⎤ J L 3 = b 2 × r 2 , e = ∣ i j k 0 0 1 l 3 c θ 123 l 3 s θ 123 0 ∣ = [ − l 3 s θ 123 l 3 c θ 123 0 ] J_{L3}=b_2\times r_{2,e}=\left|\begin{matrix}i&j&k\\0&0&1\\l_3c\theta_{123}&l_3s\theta_{123}&0\\\end{matrix}\right|=\left[\begin{matrix}-l_3s\theta_{123}\\l_3c\theta_{123}\\0\\\end{matrix}\right] JL3=b2×r2,e=∣∣∣∣∣∣i0l3cθ123j0l3sθ123k10∣∣∣∣∣∣=⎣⎡−l3sθ123l3cθ1230⎦⎤ J A 1 = b 0 = [ 0 0 1 ] ; J A 2 = b 1 = [ 0 0 1 ] ; J A 2 = b 2 = [ 0 0 1 ] J_{A1}=b_0=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right];J_{A2}=b_1=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right];J_{A2}=b_2=\left[\begin{matrix}0\\0\\1\\\end{matrix}\right] JA1=b0=⎣⎡001⎦⎤;JA2=b1=⎣⎡001⎦⎤;JA2=b2=⎣⎡001⎦⎤ J = [ J L 1 J L 2 J L 3 J A 1 J A 2 J A 3 ] = [ − l 1 s θ 1 − l 2 s θ 12 − l 3 s θ 123 − l 2 s θ 12 − l 3 s θ 123 − l 3 s θ 123 l 1 c θ 1 + l 2 c θ 12 + l 3 c θ 123 l 2 c θ 12 + l 3 c θ 123 l 3 c θ 123 0 0 0 0 0 0 0 0 0 1 1 1 ] J=\left[\begin{matrix}J_{L1}&J_{L2}&J_{L3}\\J_{A1}&J_{A2}&J_{A3}\\\end{matrix}\right]=\left[\begin{matrix}-l_1s\theta_1-l_2s\theta_{12}-l_3s\theta_{123}&-l_2s\theta_{12}-l_3s\theta_{123}&-l_3s\theta_{123}\\l_1c\theta_1+l_2c\theta_{12}+l_3c\theta_{123}&l_2c\theta_{12}+l_3c\theta_{123}&l_3c\theta_{123}\\0&0&0\\0&0&0\\0&0&0\\1&1&1\\\end{matrix}\right] J=[JL1JA1JL2JA2JL3JA3]=⎣⎢⎢⎢⎢⎢⎢⎡−l1sθ1−l2sθ12−l3sθ123l1cθ1+l2cθ12+l3cθ1230001−l2sθ12−l3sθ123l2cθ12+l3cθ1230001−l3sθ123l3cθ1230001⎦⎥⎥⎥⎥⎥⎥⎤ 可以简写为 J = [ − l 1 s θ 1 − l 2 s θ 12 − l 3 s θ 123 − l 2 s θ 12 − l 3 s θ 123 − l 3 s θ 123 l 1 c θ 1 + l 2 c θ 12 + l 3 c θ 123 l 2 c θ 12 + l 3 c θ 123 l 3 c θ 123 1 1 1 ] J=\left[\begin{matrix}-l_1s\theta_1-l_2s\theta_{12}-l_3s\theta_{123}&-l_2s\theta_{12}-l_3s\theta_{123}&-l_3s\theta_{123}\\l_1c\theta_1+l_2c\theta_{12}+l_3c\theta_{123}&l_2c\theta_{12}+l_3c\theta_{123}&l_3c\theta_{123}\\1&1&1\\\end{matrix}\right] J=⎣⎡−l1sθ1−l2sθ12−l3sθ123l1cθ1+l2cθ12+l3cθ1231−l2sθ12−l3sθ123l2cθ12+l3cθ1231−l3sθ123l3cθ1231⎦⎤ 采用牛顿-欧拉方法建立图示机器人杆件的动力学方程,并附图示。 (15 分) 因杆件是平面机构惯性张量,可用标量I_i;表示。杆件1的牛顿-欧拉方程可以表示为 0 f 1 − 1 f 2 + m 1 g − m 1 • v c 1 = 0 ( 6 − 1 ) {{^0}f}_1-{{^1}f}_2+m_1g-m_1•v_{c1}=0(6-1) 0f1−1f2+m1g−m1•vc1=0(6−1) 0 n 1 − 1 n 2 + 1 p c 1 × 1 f 2 − 0 p c 1 × 0 f 1 − I 1 • ω 1 = 0 ( 6 − 2 ) {{^0}n}_1-{{^1}n}_2+{{^1}p}{c1}\times{{^1}f}_2-{{^0}p}{c1}\times{{^0}f}_1-I_1•ω1=0 (6-2) 0n1−1n2+1pc1×1f2−0pc1×0f1−I1•ω1=0(6−2) 杆件2的牛顿-欧拉方程可以表示为 1 f 2 − 2 f 3 + m 2 g − m 2 • v c 2 = 0 ( 6 − 3 ) {{^1}f}_2-{{^2}f}_3+m_2g-m_2•vc2=0 (6-3) 1f2−2f3+m2g−m2•vc2=0(6−3) 1 n 2 − 2 n 3 + 2 p c 2 × 2 f 3 − 1 p c 2 × 1 f 2 − I 2 • ω 2 = 0 ( 6 − 4 ) {{^1}n}_2-{{^2}n}_3+{{^2}p}_{c2}\times{{^2}f}_3-{{^1}p}_{c2}\times{{^1}f}_2-I_2•ω2=0 (6-4) 1n2−2n3+2pc2×2f3−1pc2×1f2−I2•ω2=0(6−4) 杆件3的牛顿-欧拉方程可以表示为 2 f 3 + m 3 g − m 3 • v c 3 = 0 ( 6 − 5 ) {{^2}f}_3+m_3g-m_3•vc3=0 (6-5) 2f3+m3g−m3•vc3=0(6−5) 2 n 3 − 2 p c 3 × 2 f 3 − I 3 • ω 3 = 0 ( 6 − 6 ) {{^2}n}_3-{{^2}p}_{c3}\times{{^2}f}_3-I_3•ω3=0 (6-6) 2n3−2pc3×2f3−I3•ω3=0(6−6)
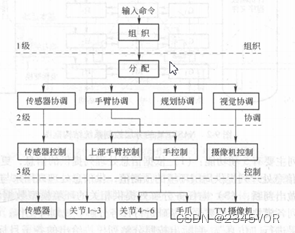
图 2三个杆件手臂的质量参数 2.4 传感器 如若图示机械手用于装配作业,负载 5Kg,识别精度 2mm,需配置哪些类型的传感装置?(10分) 机械手用于装配作业,需配置内部状态信息传感器和检测外部对象及外部环境状态的外部信息传感器。内部信息传感器包括检测位置、速度、力、力矩、温度以及异常变化的传感器。外部信息传感器包括视觉传感器、触觉传感器、力觉传感器、接近觉传感器传感器等。 请设计图示机械手用于装配时的智能控制结构,附图说明。 (15 分)智能控制系统分为3级,即组织级、协调级和控制级也称执行级。 组织级:接受任务命令,解释命令,并根据系统其他部分的反馈信息,确定任务,表达任务,把任务分解成系统可以执行的若干子任务。因此,组织级应具有任务表达,对任务的规划、决策和学习的功能。它是智能控制系统中,智能能力最强,控制精度最低级。 协调级:接受组织级的指令和子任务执行过程的反馈信息,来协调下一层的执行,确定执行的序列和条件。这一级要有决策、调度的功能,也要具有学习的功能。 控制级:功能是执行确定的运动和提供明确的信息,同时要满足协调级提出的终止条件和行为评价标准。最优控制或者近似最优控制理论会在这一层发挥作用。这一级是智能控制系统中控制精度最高,智能最低的一级。
图 3机器人的3级智能控制结构 2.5 编程题编写机器人程序(编程语言不限),通过图示机械手将一块积木从 A 处拾起放到 B 处。 (A,B两点不在同一平面改为两点的x,y坐标完全不同,坐标可自行设定)。 (15 分) 设置A处坐标为(50,250)记为PICK位置,B处坐标为(250,50)记为PLACE位置。下面是一个程序名为DEMO的VAL程序,其功能是将物体从位置A (PICK位置)搬运至位置2 (PLACE位置)。 ABB机器人为例 EDIT DEMO 启动编辑状态 PROGRAM DEMO VAL响应 OPEN 下一步手张开 APPRO PICK 60 运动至距PICK位置60mm处 SPEED20 下一步降至20%满速 MOVE PICK 运动至PICK位置 CLOSEI 闭合手 DEPART 70 沿手矢量方向后退70mm APPROS PLACE 75 沿直线运动至距离PLACE位置75mm处 SPEED 20 下步降至20%满速 MOVES PLACE 沿直线运动至PLACE位置上 OPENI 在下一步之前手张开 DEPART 50 自PLACE位置后退50mm E 退出编辑状态返回监控状态 |
【本文地址】
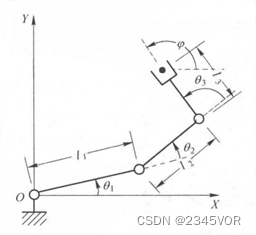
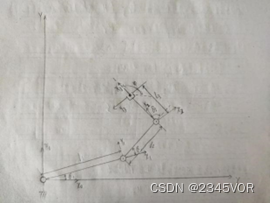 图 1机械手各附体坐标系
图 1机械手各附体坐标系