|
  最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 基本公式 考虑超定方程组(超定指方程个数大于未知量个数): 最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 基本公式 考虑超定方程组(超定指方程个数大于未知量个数): 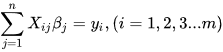 其中m代表有m个等式,n代表有n个未知数β,m>n ;将其进行向量化后为:Xβ=y 其中m代表有m个等式,n代表有n个未知数β,m>n ;将其进行向量化后为:Xβ=y 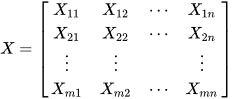  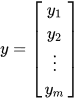 显然该方程组一般而言没有解,所以为了选取最合适的β让该等式"尽量成立",引入残差平方和函数S 显然该方程组一般而言没有解,所以为了选取最合适的β让该等式"尽量成立",引入残差平方和函数S 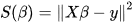  方法 以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。 方法 以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择: (1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。 (2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。 (3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。 最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即采用平方损失函数。
样本回归模型:(其中ei为样本(Xi,Yi)的误差) 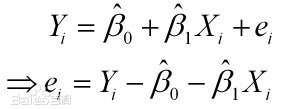 平方损失函数: 平方损失函数: 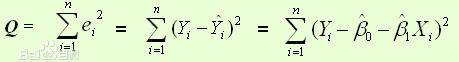 则通过Q最小确定这条直线,即确定β0和β1,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数: 则通过Q最小确定这条直线,即确定β0和β1,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数: 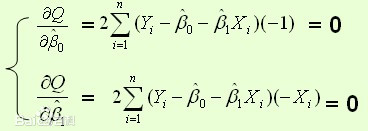 根据数学知识我们知道,函数的极值点为偏导为0的点。 解得: 根据数学知识我们知道,函数的极值点为偏导为0的点。 解得: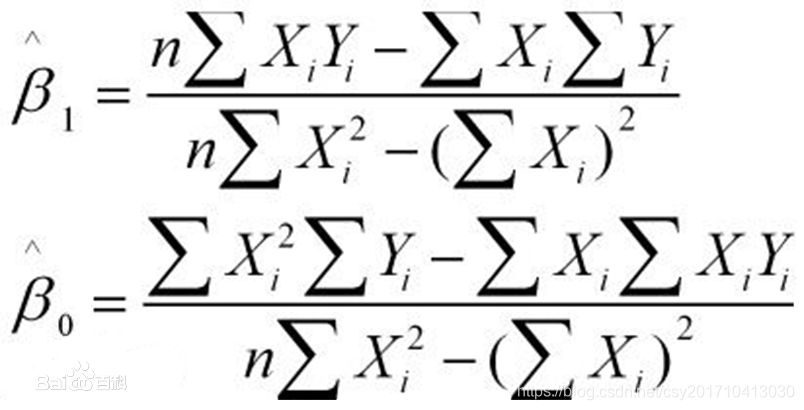 这就是最小二乘法的解法,就是求得平方损失函数的极值点。 这就是最小二乘法的解法,就是求得平方损失函数的极值点。
梯度下降法(英语:Gradient descent)是一个一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。 我们给出线性回归的损失函数,为了方便,不带正则项: 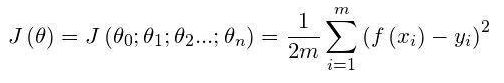 其中 其中  具体的梯度下降流程: 第一步:先随便假设一组θ,你要是喜欢可以全部取0 第二步循环迭代: 第一次迭代: 具体的梯度下降流程: 第一步:先随便假设一组θ,你要是喜欢可以全部取0 第二步循环迭代: 第一次迭代: 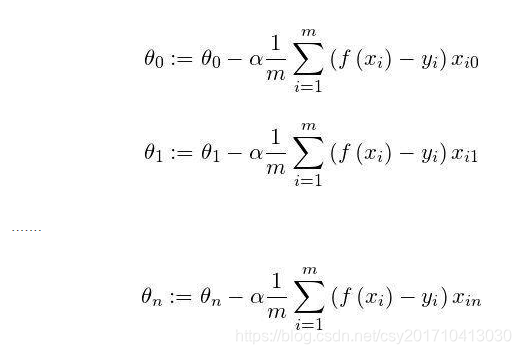 第二次迭代: 第二次迭代:  … 第x次迭代:… 第三步,满足要求,循环结束,得到θ 最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么异同? 相同: 1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。 2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为: … 第x次迭代:… 第三步,满足要求,循环结束,得到θ 最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么异同? 相同: 1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。 2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为: 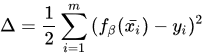  不同: 1.实现方法和结果不同:最小二乘法是直接对Δ求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个β,然后向Δ下降最快的方向调整β,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。 牛顿法 牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f(x)=0的根。牛顿法最大的特点就在于它的收敛速度很快。 用牛顿迭代法解非线性方程,是把非线性方程f(x)=0线性化的一种近似方法。把f(x)在点x0的某邻域内展开成泰勒级数 不同: 1.实现方法和结果不同:最小二乘法是直接对Δ求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个β,然后向Δ下降最快的方向调整β,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。 牛顿法 牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f(x)=0的根。牛顿法最大的特点就在于它的收敛速度很快。 用牛顿迭代法解非线性方程,是把非线性方程f(x)=0线性化的一种近似方法。把f(x)在点x0的某邻域内展开成泰勒级数 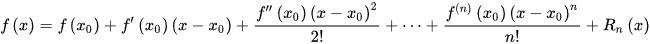 取其线性部分(即泰勒展开的前两项),并令其等于0,即 取其线性部分(即泰勒展开的前两项),并令其等于0,即 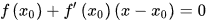 以此作为非线性方程f(x)=0的近似方程,若 以此作为非线性方程f(x)=0的近似方程,若 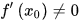 则其解为 则其解为 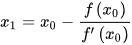 得到牛顿迭代法的一个迭代关系式: 得到牛顿迭代法的一个迭代关系式: 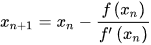 已经证明,如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。 已经证明,如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
高斯牛顿法 高斯一牛顿迭代法(Gauss-Newton iteration method)是非线性回归模型中求回归参数进行最小二乘的一种迭代方法,该法使用泰勒级数展开式去近似地代替非线性回归模型,然后通过多次迭代,多次修正回归系数,使回归系数不断逼近非线性回归模型的最佳回归系数,最后使原模型的残差平方和达到最小。其直观思想是先选取一个参数向量的参数值β,若函数ft(Xt,β)在β0附近有连续二阶偏导数,则在β0的邻域内可近似地将ft(Xt,β)看作是线性,因而可近似地用线性最小二乘法求解 高斯-牛顿法的一般步骤如下所示 (1) 初始值的选择。其方法有三种: 一是根据以往的经验选定初始值; 二是用分段法求出初始值; 三是对于可线性化的非线性回归模型,通过线性变换,然后施行最小平方法求出初始值 (2)泰勒级数展开式。设非线性回归模型为 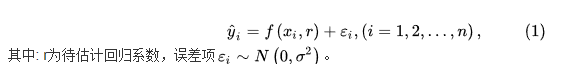  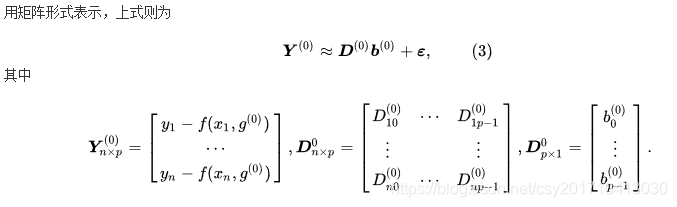  最小二乘法C++实现 最小二乘法C++实现
/*
最小二乘法C++实现
参数1为输入文件
输入 : x
输出: 预测的y
*/
#include
#include
#include
using namespace std;
class LeastSquare{
double a, b;
public:
LeastSquare(const vector& x, const vector& y)
{
double t1=0, t2=0, t3=0, t4=0;
for(int i=0; i
return a*x + b;
}
void print() const
{
cout
cout
cout | 
 最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 基本公式 考虑超定方程组(超定指方程个数大于未知量个数):
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 基本公式 考虑超定方程组(超定指方程个数大于未知量个数): 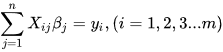 其中m代表有m个等式,n代表有n个未知数β,m>n ;将其进行向量化后为:Xβ=y
其中m代表有m个等式,n代表有n个未知数β,m>n ;将其进行向量化后为:Xβ=y 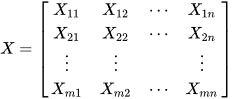

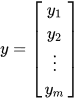 显然该方程组一般而言没有解,所以为了选取最合适的β让该等式"尽量成立",引入残差平方和函数S
显然该方程组一般而言没有解,所以为了选取最合适的β让该等式"尽量成立",引入残差平方和函数S 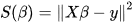
 方法 以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。
方法 以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。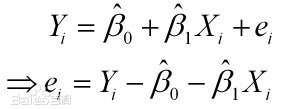 平方损失函数:
平方损失函数: 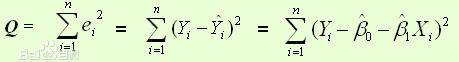 则通过Q最小确定这条直线,即确定β0和β1,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
则通过Q最小确定这条直线,即确定β0和β1,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数: 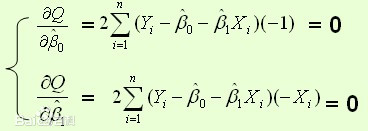 根据数学知识我们知道,函数的极值点为偏导为0的点。 解得:
根据数学知识我们知道,函数的极值点为偏导为0的点。 解得: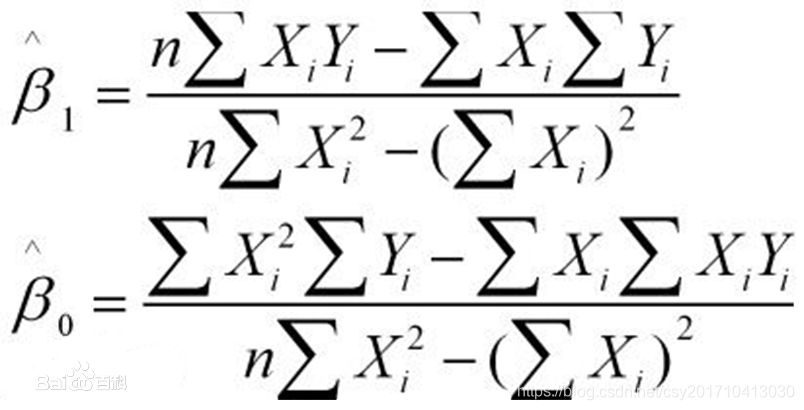 这就是最小二乘法的解法,就是求得平方损失函数的极值点。
这就是最小二乘法的解法,就是求得平方损失函数的极值点。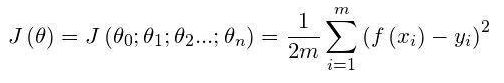 其中
其中  具体的梯度下降流程: 第一步:先随便假设一组θ,你要是喜欢可以全部取0 第二步循环迭代: 第一次迭代:
具体的梯度下降流程: 第一步:先随便假设一组θ,你要是喜欢可以全部取0 第二步循环迭代: 第一次迭代: 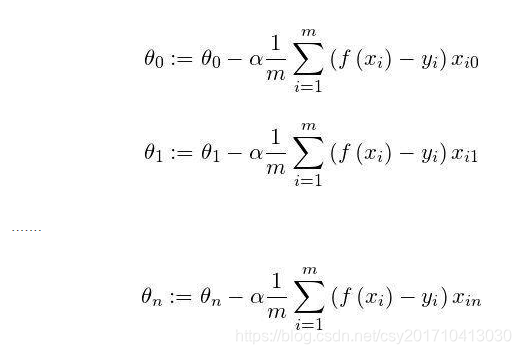 第二次迭代:
第二次迭代:  … 第x次迭代:… 第三步,满足要求,循环结束,得到θ 最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么异同? 相同: 1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。 2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为:
… 第x次迭代:… 第三步,满足要求,循环结束,得到θ 最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么异同? 相同: 1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。 2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为: 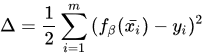
 不同: 1.实现方法和结果不同:最小二乘法是直接对Δ求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个β,然后向Δ下降最快的方向调整β,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。 牛顿法 牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f(x)=0的根。牛顿法最大的特点就在于它的收敛速度很快。 用牛顿迭代法解非线性方程,是把非线性方程f(x)=0线性化的一种近似方法。把f(x)在点x0的某邻域内展开成泰勒级数
不同: 1.实现方法和结果不同:最小二乘法是直接对Δ求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个β,然后向Δ下降最快的方向调整β,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。 牛顿法 牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f(x)=0的根。牛顿法最大的特点就在于它的收敛速度很快。 用牛顿迭代法解非线性方程,是把非线性方程f(x)=0线性化的一种近似方法。把f(x)在点x0的某邻域内展开成泰勒级数 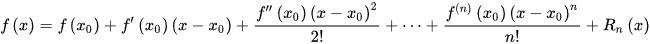 取其线性部分(即泰勒展开的前两项),并令其等于0,即
取其线性部分(即泰勒展开的前两项),并令其等于0,即 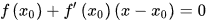 以此作为非线性方程f(x)=0的近似方程,若
以此作为非线性方程f(x)=0的近似方程,若 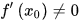 则其解为
则其解为 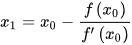 得到牛顿迭代法的一个迭代关系式:
得到牛顿迭代法的一个迭代关系式: 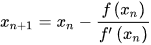 已经证明,如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
已经证明,如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。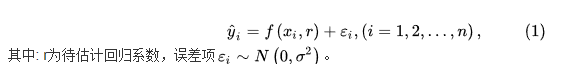

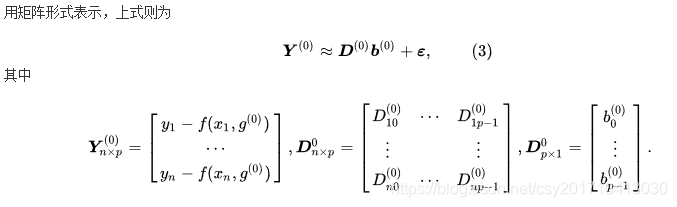
 最小二乘法C++实现
最小二乘法C++实现