| 最优化理论复习 | 您所在的位置:网站首页 › 最优化理论期末考试 › 最优化理论复习 |
最优化理论复习
|
文章目录
基本概念凸集凸函数下一篇
基本概念
可行点(可行解):在规划问题中,满足约束条件的点可行集或可行域:全体可行点组成的集合无约束问题:如果一个问题的可行集是整个空间。
分为三种情况: S = ∅ , 则 称 该 问 题 无 解 或 不 可 行 S = \emptyset, 则称该问题无解或不可行 S=∅,则称该问题无解或不可行 S ≠ ∅ , 但 是 目 标 函 数 在 S 上 无 界 S \not = \emptyset, 但是目标函数在S上无界 S=∅,但是目标函数在S上无界 S ≠ ∅ 且 目 标 函 数 有 限 的 最 优 解 , 则 称 问 题 有 最 优 解 S \not = \emptyset 且目标函数有限的最优解,则称问题有最优解 S=∅且目标函数有限的最优解,则称问题有最优解符号问题: x ∈ R n x\in R^n x∈Rn表示 x x x 是向量 x ∈ R x \in R x∈R表示 x x x 是实数 黑体的是向量 没有加粗的是数 凸集凸集定义:设S为n维欧式空间 R n R^n Rn中的一个集合。若对任意两点 x ( 1 ) , x ( 2 ) ∈ S x^{(1)}, x^{(2)} \in S x(1),x(2)∈S及每个实数 λ ∈ [ 0 , 1 ] \lambda \in [0, 1] λ∈[0,1] 有 λ ∗ x ( 1 ) + ( 1 − λ ) ∗ x ( 2 ) ∈ S \lambda * x^{(1)} + (1 - \lambda) * x^{(2)} \in S λ∗x(1)+(1−λ)∗x(2)∈S 则称S为凸集。 λ ∗ x ( 1 ) + ( 1 − λ ) ∗ x ( 2 ) \lambda * x^{(1)} + (1 - \lambda) * x^{(2)} λ∗x(1)+(1−λ)∗x(2)称为 x ( 1 ) x^{(1)} x(1)和 x ( 2 ) x^{(2)} x(2)的凸组合。 凸组合定义:给定m个向量, x 1 , x 2 , . . . , x m ∈ R n x^1, x^2,...,x^m \in R^n x1,x2,...,xm∈Rn, 以及满足 ∑ λ i = 1 \sum{\lambda_i = 1} ∑λi=1的非负实数 λ i ∈ R \lambda_i \in R λi∈R, 称向量 λ 1 x 1 + λ 2 x 2 + . . . + λ m x m \lambda_1 x^1 + \lambda_2 x^2 + ... + \lambda_m x^m λ1x1+λ2x2+...+λmxm为 x x x 的凸组合。 根据向量知识凸组合形成的集合图形为两顶点之间的连线 定理:如果S为凸集那么其中具有任意有限元素的凸组合。 凸集性质: 凸集放大 α \alpha α倍仍为凸集凸集相交仍为凸集凸集的元素求和仍为凸集凸集的元素相减仍为凸集凸包定义:凸包,给定一堆点,这堆点的凸包就是包含这些点的最小凸集。 这些点称为单纯形的顶点。 闭包: 闭集的闭包就是它本身开集的闭包就是它本身加上它的边界集凸锥定义:设有集合 C ⊂ R n C\subset R^n C⊂Rn, 若对每一点 x ∈ C x \in C x∈C,当 λ \lambda λ 取任何非负数时,都有 λ x ∈ C \lambda x \in C λx∈C, 称C为锥,如果C为凸集,则称C为凸锥。 从零点到x延长线上的点仍在集合C中 最优化理论与算法课程-西南科技大学 凸锥组合: { ∑ λ i α ( i ) ∣ λ i > = 0 , i = 1 , 2... k } \{\sum{\lambda_i \alpha^{(i)}} | \lambda_i >= 0, i = 1, 2 ...k\} {∑λiα(i)∣λi>=0,i=1,2...k} 多面集:由有限个半空间的交组成的集合为多面集 { x ∣ A x < = b } \{ x | Ax x+λd∣λ>=0}⊂S则称向量 d d d 为S的方向。 极方向:如果方向 d d d 无法由其他两个方向的凸组合得到,那么方向d就是凸锥的极方向。(凸锥组合就是两个方向中夹角的一个方向,向量加法) 性质定理 表示定理: 凸集分离定理 设
S
1
S_1
S1和
S
2
S_2
S2是
R
n
R^n
Rn中两个非空集合,
H
=
{
x
∣
p
T
x
=
α
}
H= \{ x | p^T x = \alpha\}
H={x∣pTx=α}为超平面, 如果对
∀
x
∈
S
1
\forall x \in S_1
∀x∈S1, 都有
p
T
x
>
=
α
p^T x >= \alpha
pTx>=α, 对于每个
x
∈
S
2
x \in S_2
x∈S2, 都有
p
T
x
<
=
α
p^T x 0
ξ>0, 使得对每一个点
x
∈
S
x \in S
x∈S, 成立
p
T
y
>
=
ξ
+
p
T
x
p^T y >= \xi + p^T x
pTy>=ξ+pTx
凸集分离定理 设 S 1 S_1 S1 和 S 2 S_2 S2是 R n R^n Rn的两个非空凸集, S 1 ∩ S 2 = ∅ S_1 \cap S_2 = \emptyset S1∩S2=∅, 则存在非零向量 p p p, 使得 i n f { p T ∣ x ∈ S 1 } > = s u p { p T x ∣ x ∈ S 2 } inf \{p^T | x \in S_1 \} >= sup \{ p^T x | x \in S_2\} inf{pT∣x∈S1}>=sup{pTx∣x∈S2} 两个交集非空的凸集一定能找到一个超平面将他们分离 择一定理 不等式组解的充分必要条件 Farkas定理 设A为m x n矩阵, c为n维向量,则 A x < = 0 , c T x > 0 Ax 0 Ax0有解的充分必要条件是 A T y = c , y > = 0 A^T y = c, y >= 0 ATy=c,y>=0无解。Gordan引理 设A为m x n矩阵,那么,Ax < 0 有解的充分条件是不存在非零向量 y >= 0, 使 A T y = 0 A^T y = 0 ATy=0 凸函数凸函数定义:设S是 R n R^n Rn 中的非空凸集, f ( x ) f(x) f(x) 是定义在S上的实函数,如果对于每一对 x 1 , x 2 ∈ S x_1, x_2 \in S x1,x2∈S 及每一个 a a a, 0 < = a < = 1 0 就是严格凸
二阶充要条件: 设
S
S
S 是
R
n
R^n
Rn 中非空开凸集,
f
(
x
)
f(x)
f(x) 是定义在S上的二次可微函数,则
f
(
x
)
f(x)
f(x)为凸函数的充要条件是对任意
x
∈
S
x \in S
x∈S,
f
(
x
)
f(x)
f(x) 在x 处的 Hessian矩阵
▽
2
f
(
x
)
\bigtriangledown^2 f(x)
▽2f(x)是半正定的。 对二次函数, 正定为严格凸函数。 半正定为凸函数。 最优化理论复习–线性规划性质 |
【本文地址】

 即多面集可以由极点的凸组合和极方向的凸锥组合全部表示出来
即多面集可以由极点的凸组合和极方向的凸锥组合全部表示出来 可以在点和凸集中间找到一个超平面
可以在点和凸集中间找到一个超平面
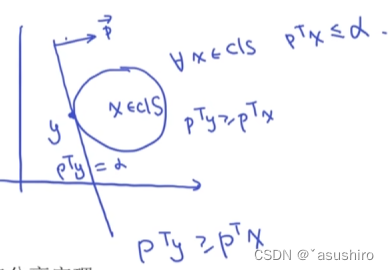 考虑边界的情况
考虑边界的情况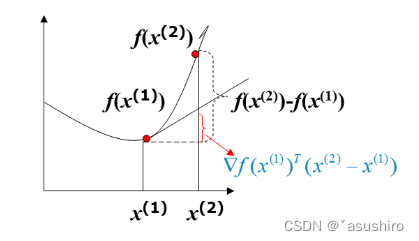 f
(
x
)
f(x)
f(x)是凸函数当且仅当任意点处的切线增量不超过函数增量
f
(
x
)
f(x)
f(x)是凸函数当且仅当任意点处的切线增量不超过函数增量