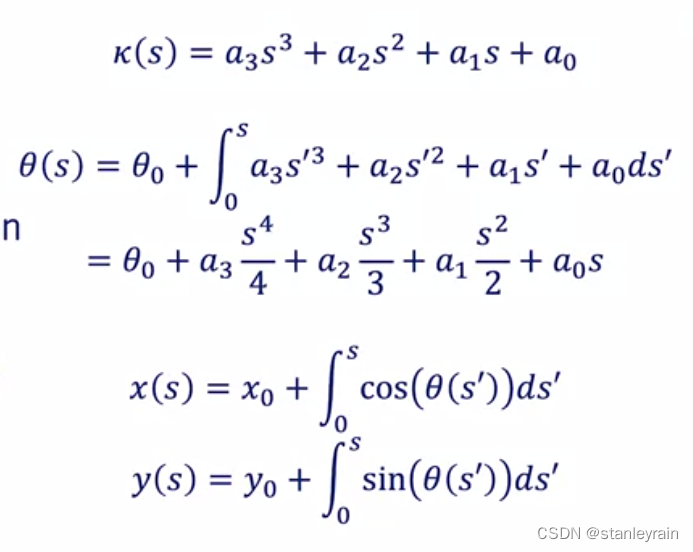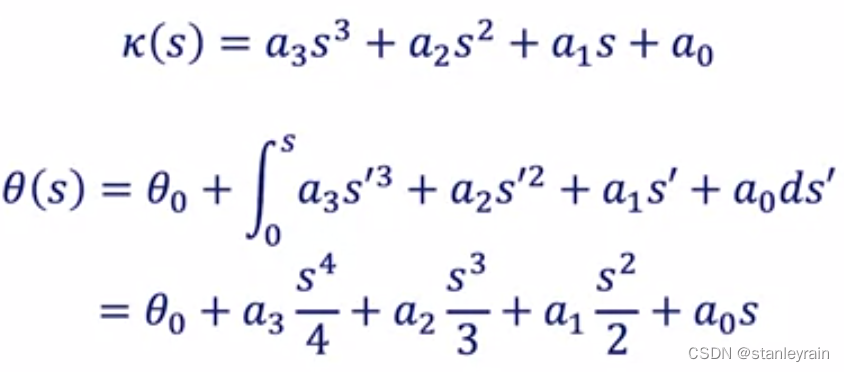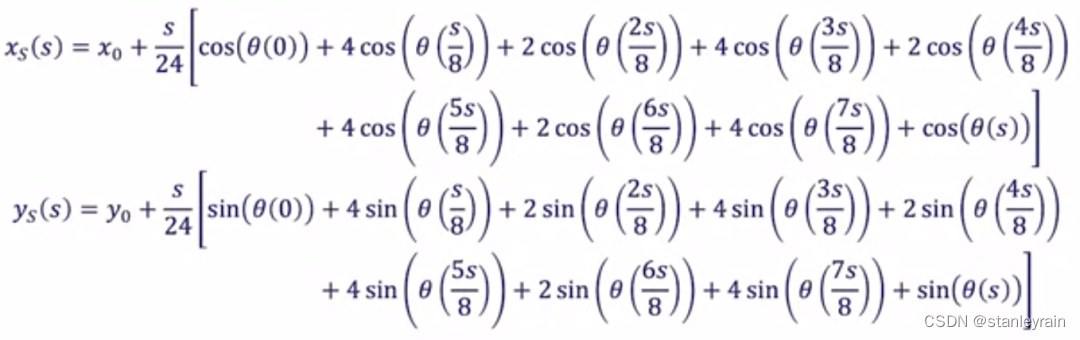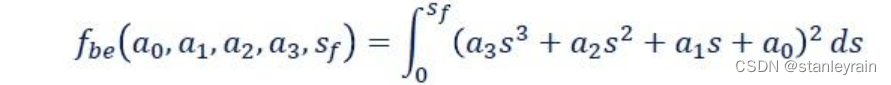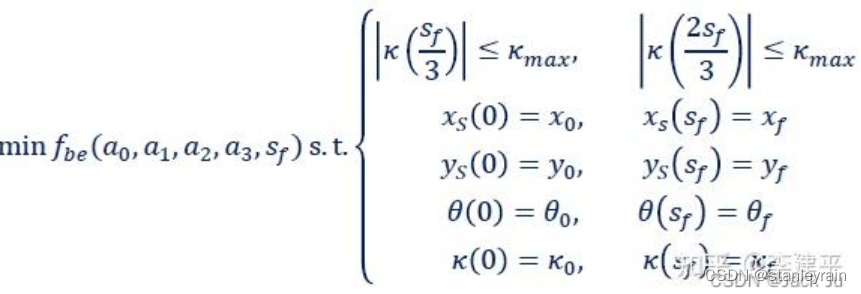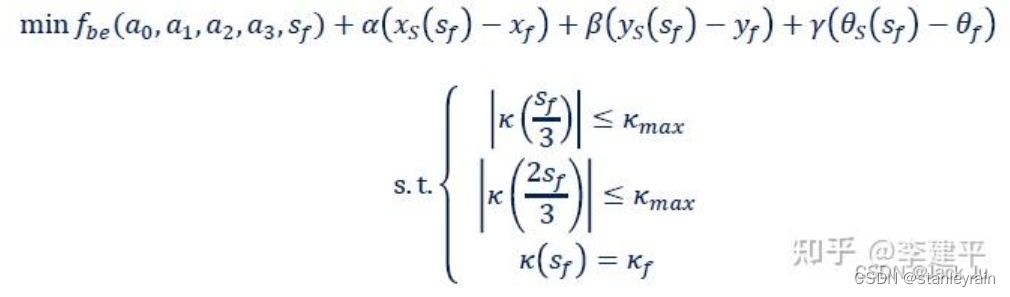无人驾驶中局部路径规划之螺旋多项式解释及说明（优化问题及其核心求解算法的最简表述）（梯度下降及牛顿法的区别）

您所在的位置：网站首页 › 曲率公式三种表达式怎么写 › 无人驾驶中局部路径规划之螺旋多项式解释及说明（优化问题及其核心求解算法的最简表述）（梯度下降及牛顿法的区别）

无人驾驶中局部路径规划之螺旋多项式解释及说明（优化问题及其核心求解算法的最简表述）（梯度下降及牛顿法的区别）

2024-07-12 17:04| 来源: 网络整理| 查看: 265

1. 核心思想

给定路径上的两个点，起点和终点，找出一条符合路径约束，车辆动力学约束，车辆舒适性约束等约束的路径。

在上面的表述中，需要使用数学表达式表达起点，终点的概念，螺旋多项式的数学表达式，以及最终的求解方法。由于该问题是一个带约束的数学表达式，一般采用牛顿求根法进行。

2. 问题的具体数学表达式

文章Local Planning Path-三次螺旋曲线-腾讯云开发者社区-腾讯云很好的描述了整个过程，但是，由于作者水平很高，很多地方描述的很简略，以至于对初学者读起来晦涩难懂，本文就是帮助读者对上面的文章进行理解。

学习过程中，也可以参考文章自动驾驶——Smooth Local Planning_5次样条曲线-CSDN博客，该文章进行了更为详细和准确的表述。

车辆起点的状态包含了 (x0,y0,θ0,k0)，其含义分别是：

( x_0 ) 和 ( y_0 )：这两个值代表车辆在平面坐标系中的初始位置，其中 ( x_0 ) 表示车辆在水平方向（通常是沿着道路或路径）的位置，而 ( y_0 ) 则表示车辆在垂直方向的位置。

( \theta_0 )：这个值表示车辆初始时的朝向角度，通常用于描述车辆的方向，例如相对于道路的朝向。

( k_0 )：这是初始时的曲率或曲率半径。曲率描述了路径的弯曲程度，曲率半径则是曲率的倒数。在车辆运动中，曲率或曲率半径的变化影响了车辆的转弯半径和转弯速度。

多项式螺旋曲线可以表示为：

k(s)=a0+a1∗s+a2∗s2+a3∗s3

其中，k为曲率，s为弧长。上面的公式可以理解为，对于路径上的某一点，其曲率为该点从原点（路径起始点）到该点的弧长的多项式，这里是三次多项式。注意：弧长的概念是指从平面上一点到另外一点所经过的曲线的路径的长度。如一个圆形上的两个点，其弧长就是连接两点的弧的长度，注意弧长与弧度的概念的区别。弧度是圆的曲线（弧长）与半径的比值，一个圆的弧度就是2π。

给定上述多项式螺旋曲线后，因此，就可以求出路径上任意一点的坐标，方向和曲率，具体公式如下：

上图中，k表示曲率， $\theta$ 表示该点的角度，x，y表示该点的坐标。因此，只要确定了螺旋式曲线的系数 $a_0, a_1, a_2$ ,知道弧长，就能确定该点的所有信息。

辛普森公式（Simpson's Rule）

在上图中，需要对定积分进行求解，因此，需要找出定积分求解的方法，一种方法就是使用辛普森公式进行近似，具体地：

因此，有：

注意：图中的辛普森公式将积分分为8段，根据公式h=（b-a）/n，这里，b=s， a=0，因此有h=（s-0）/8/3，所以有s/24。上述图片，在本文中引用时，使用“路径公式”描述。

边界约束条件（Coundary Condition）

车辆的终点，必须满足车辆的终点的条件

曲率约束

路径上的点，必须满足车辆的最小转弯半径，即：路径上的曲线的曲率不能超过一定的范围。

以上，便完成了问题的数学表达式。问题可以描述为：

寻找参数 $a_0, a_1, a_2$ ，使得路径公式满足边界条件约束和路径曲率约束。

另外，由于车辆运行中，需要平滑的运行，因此，通过“弯曲能量”这个概念来进行表述，“弯曲能量”是指对曲线的曲率平方进行积分的结果，如下图所示：

f_be即为“弯曲能量”。

因此，整个数学表达式可以表示为：

由于最终的终点不一定可以满足，因此，可以将上述的条件转换为软约束，公式如下：

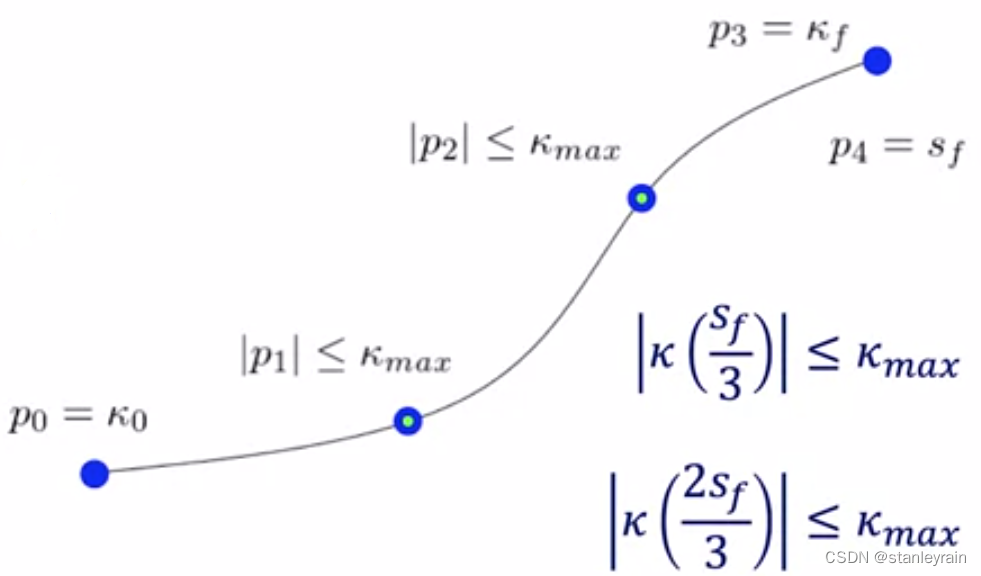
为了能更快地求解，进行了参数的重映射，即：将问题需要求解的a_0, a_1, a_2, a_3等转换为路径上的点的曲率p0, p1, p2,p3, 分别表示起点，1/3, 2/3, 终点的曲率，p4为最终的弧长。

通过上面，优化问题，最终转换为求解p1， p2和p4，其中，p0和p3是已经给定的。通过转换，减低了求解空间的维数，可以加快计算。

所以，最终求解问题转换为：

3. 问题的求解

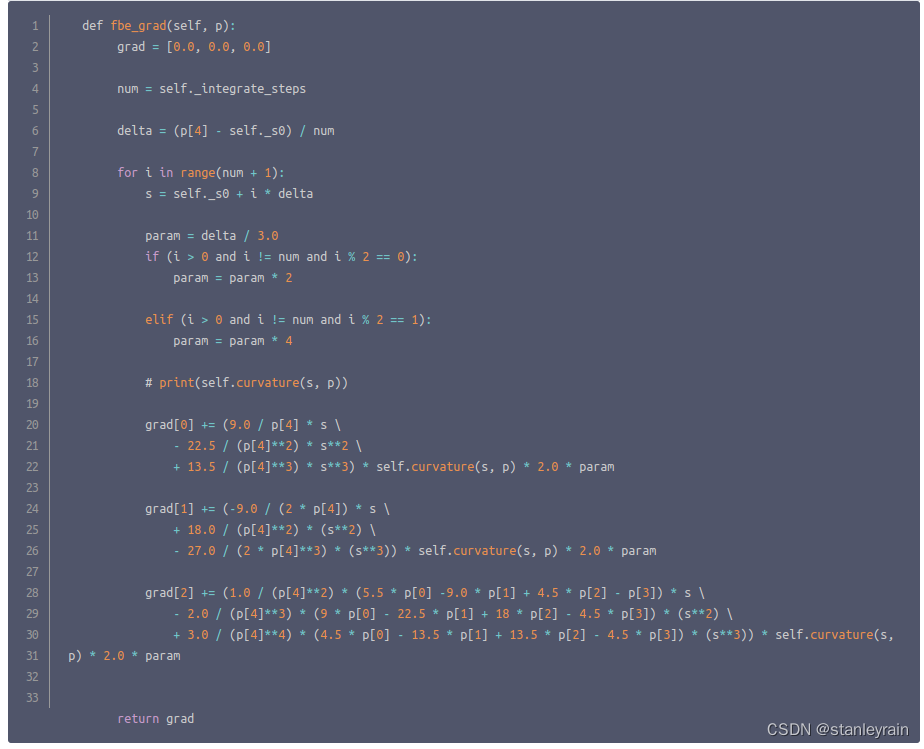
上述问题本质上是一个优化问题，因此，可以使用机器学习的优化算法进行求解。

理论上，可以参考文章https://blog.csdn.net/anshuai_aw1/article/details/86667931

Jacobian矩阵和Hessian矩阵，LM最优化方法_二次函数的梯度和hessian矩阵-CSDN博客

3.1 梯度下降

假定有一个函数y=f（x），想要找到函数y=f（x）的最小值，即y的最小值，梯度下降的核心是：

假定从任意的一点x_0开始，此时，y = y_0开始寻找，我们只要保证下一次的点y_1小于上一次的点y_0就可以找到最小值。问题是，如何能保证下一次找到的y_1小于上一次的点呢？

这里，需要用到一个数学知识，假定已知x的值，给x加上一个小的值 $\Delta x$ ，函数值y的值为

$y + \Delta y = f(x) + f{}' \Delta x$

上面公式的含义即：x的值变化一点点 $\Delta x$ ，则y的值也变化一点点 $\Delta y$ ，y的值的变化 $\Delta y$ 等于

$\Delta y = f{}'\Delta x$

其中， $\Delta y$ 是应变量y随着自变量x的变化 $\Delta x$ 的变化， f’是一阶倒数。

从上面公式中，可以知道，假定 $\Delta x$ 是一个正数，则 $\Delta y$ 是正还是负是由f(x)的一阶倒数f’来确定的。

由此可知，要想求解下一次y_1, 则只有保证 $\Delta y$ 是负的，因为：

y_1 = y_0 + $\Delta y$

所以，令：

$\Delta y = - f{}'\Delta x$

则可以保证y的值是不断减小的，并最终找到最小值。

3.2 牛顿法

对于一个函数f(x)，求解其最小值，其方法为：

f(x_0)是一个极小值，则其一阶倒数f'(x_0) = 0，只要找到使得f'(x)为0的x的值，则f（x）为极小值。

已知：

$f'(x + \Delta x) = f'(x) + f''(x) (x+\Delta x)$

令 $f'(x+\Delta x) = 0$ , 所以有：

$f'(x) + f''(x) \Delta x = 0$

所以，

$\Delta x = - (f'(x) / f''(x))$

因此，通过对x的迭代，可以获得f(x)的最小值。

3.3 螺旋式多项式的求解

对于螺旋多项式求解问题，其目标函数为：

$min(f_{be}(a_0, a_1, a_2, a_3, s_f) + \alpha (x_s(s_f) - x_f))^2 + \beta (y_s(s_f) - y_f)^2 + \gamma (\theta _s(s_f) - \theta_f))^2$

注意：需要将目标函数中的a_0, a_1, ... 等替换为p_0, p_1, ...，然后计算雅各比矩阵，使用梯度算法进行迭代优化。

这里的雅各比矩阵，即函数对各个变量的偏导数，这里的函数由三部分组成，变量有三个，分布是p1，p2, sf, 所以，有三个偏导数。又由于目标函数由四部分和组成，因此，需要将目标函数的各个部分，对每个变量（共三个）的偏导数求和，即可获得雅各比矩阵，如文章中代码所示。

def objective(self, p): p = [0.0, p[0], p[1], 0.0, p[2]] return self.fbe(p) + 25.0 * (self.fxf(p)**2.0 + self.fyf(p)**2.0) + 30.0 * self.ftf(p)**2.0

这个代码是用来求解总的雅各比函数的。

这个是f_be的雅各比函数，看返回值为一个3维的数组，这是由于对3个变量，求偏导的返回结果。

由于函数实在太过于长，我也没有想法手工计算作者给出的算式是否正确，总之，作者为了程序实现简洁，直接给出了偏导的表达式，我就假定它是正确的了，有兴趣的小伙伴可以演算以验证其正确性。

另外，由于水平有限，有些表述不正确，还请指出。另外，如果有原理性错误，也请各位大拿在留言区指出，您的指正，将会帮助更多人更快的学习，感激不尽！

【本文地址】

公司简介

联系我们