卡方分布的性质及应用

您所在的位置：网站首页 › 显著性水平为005的f分布表 › 卡方分布的性质及应用

卡方分布的性质及应用

2024-07-01 12:00| 来源: 网络整理| 查看: 265

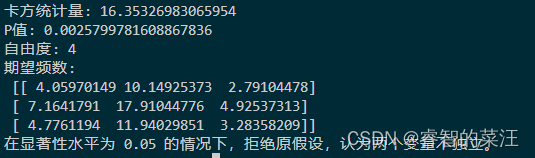
卡方分布是统计学常用的分布之一。其定义为：若N个相互独立的随机变量 $X_1,X_2,...X_n$ 均服从标准正态分布，则这N个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布。

性质

卡方分布有一些比较常用的性质。

性质1：若 $\chi^2 (v_1),\chi^2 (v_2)$ 相互独立，则 $\chi^2 (v_1)+\chi^2 (v_2)$ 也服从卡方分布，其自由度为 $v_1+v_2$ .

这个性质有比较经典的应用，在统计学中，样本均值 $\bar X=\frac{\sum_{i=1}^n{X_i}}{n}$ 和样本方差 $S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar X)^2$ 是相互独立的，

若该分布的期望为 $\mu$ 方差为 $\sigma$ ，那么可以知道：

$\bar X \sim N(\mu,\frac{\sigma^2}{n})$ ,那么， $\frac{\bar X-\mu}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0,1)$

所以 $(\frac{\bar X-\mu}{\sqrt{\frac{\sigma^2}{n}}})^2 \sim \chi (1)$

我们又知道， $\frac{(n-1)S^2}{\sigma^2} \sim \chi(n-1)$

两者又相互独立，所以， $\frac{(n-1)S^2}{\sigma^2}+(\frac{\bar X-\mu}{\sqrt{\frac{\sigma^2}{n}}})^2 \sim \chi(n)$

性质2：若 $\chi^2 (v)$ 的自由度为 $v$ ，那么 $E(\chi^2 (v))=v$

证明如下：当自由度为1时，已知 $X \sim N(0,1)$

X的密度函数为 $f_X(x)=\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}$

那么

$E(X^2)=\int_{-\infty}^{+\infty }x^2\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}dx=2\int_{0}^{+\infty\ }x^2\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}dx=[-2x\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}]|_{0}^{+\infty}+2\int_{0}^{+\infty}{\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}}dx=1$

所以 $E(\chi^2 (1))=1$

由于 $\chi^2(v)$ 之间相互独立，也满足期望 $E(X_1+X_2)=E(X_1)+E(X_2)$ 的式子

那么，由上述性质1和 $E(X_1+X_2)=E(X_1)+E(X_2)$ 可知， $E(\chi^2 (v))=v$ ，得证。

性质3：若 $\chi^2 (v)$ 的自由度为 $v$ ，那么 $D(\chi^2 (v))=2v$

证明如下：同样还是当自由度为1时，已知 $X \sim N(0,1)$

X的密度函数为 $f_X(x)=\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}$

那么

$E(X^4)=\int_{-\infty}^{+\infty }x^4\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}dx=2\int_{0}^{+\infty\ }x^4\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}dx=[-2x^3\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}]|_{0}^{+\infty}+6\int_{0}^{+\infty}{x^2\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}}dx=6\int_{0}^{+\infty}{x^2\frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}}dx=3E(X^2)$

那么 $E(X^4)=3$

所以 $D(\chi(1))=D(X^2)=E(X^4)-E^2(X^2)=2$

同样的，由于相互独立，满足 $D(X_1+X_2)=D(X_1)+D(X_2)$ ，且由性质1，知可以推广到n阶，于是 $D(\chi^2 (v))=2v$ ，得证。

应用

卡方分布有着比较广泛的应用，以下是4个比较常用的应用场景：

独立性检验：检验两个分类变量是否相互独立。拟合优度检验：检验实际观测值与理论分布的一致性。同质性检验：检验多个样本是否来自同一总体。相关性检验：在某些情况下，卡方分布可以用来检验变量之间的相关性应用场景1

独立性检验：假设我们想要检验教育水平和职业选择是否独立。我们收集了不同教育背景（高中以下、大学、研究生）人群的职业选择数据（蓝领、白领、自由职业者）。通过构建列联表和进行卡方独立性检验，我们可以确定教育水平是否影响职业选择。

假设我们收集了以下的数据：

教育水平\职业选择蓝领白领自由职业者总计高中及以下105217大学520530研究生115420总计16401167 步骤一：假设提出

原假设 $H_0$ ：教育水平和职业选择是独立的

备择假设 $H_1$ ：教育水平和职业选择是不独立的

步骤二：计算期望频数（Eij）

期望频数的计算公式为 $E_{ij}=\frac{Row_i*Col_j}{Sum}$

其中 $Row_i$ 表示第i行的行总和， $Col_j$ 表示第j列的列总和， $Sum$ 表示总计

比如 $E_{11}=17*16/67\approx 4.06$

步骤三：计算卡方统计量

使用以下公式计算卡方统计量：

$\chi^2=\sum{\frac{(O_{ij}-E_{ij})^2}{E_{ij}}}$

其中 $O_{ij}$ 表示第i行第j列的观测值， $E_{ij}$ 为步骤二中计算出来的值

例如： $\chi^2_{11}=(10-4.06)^2/4.06 \approx 8.68$

依次对所有单元格进行上述计算求和即可。

步骤四：确定自由度

这个例子中，卡方分布的自由度为行数减一乘以列数减一，即df=4，计算公式为：

$df=(Row-1)(Col-1)$

步骤五：确定p值，做出结论

选择一个合适的p值，比如0.01，再与卡方的表格进行比较即可。

这个过程可以写为python代码形式，代码如下：

import numpy as np from scipy.stats import chi2_contingency # 观测频数数据，构建列联表 # 这里使用的是之前教育水平和职业选择的示例数据 data = np.array([[10, 5, 2], [5, 20, 5], [1, 15, 4]]) # 执行卡方独立性检验 chi2, p, dof, expected = chi2_contingency(data) # 输出结果 print("卡方统计量:", chi2) print("P值:", p) print("自由度:", dof) print("期望频数:\n", expected) # 做出结论 alpha = 0.05 # 显著性水平 if p < alpha: print("在显著性水平为 {:.2f} 的情况下，拒绝原假设，认为两个变量不独立。".format(alpha)) else: print("在显著性水平为 {:.2f} 的情况下，不能拒绝原假设，认为两个变量独立。".format(alpha))

运行结果如下：

可以看到，在我们选定的显著性水平上拒绝了H0，也即教育水平和职业选择其实是有关系的。

应用场景2

拟合优度检验：一个工厂生产了一批零件，根据历史数据，我们知道合格品和次品的比例大约是95%和5%。现在，我们随机抽取了100个零件进行检查，发现有90个合格品和10个次品。我们可以使用卡方拟合优度检验来确定实际观测结果是否与预期的95%合格品比例一致。

步骤一：假设提出

原假设 $H_0$ :观测数据与理论分布一致，即合格品的比例是95%，不合格品的比例是5%

备择假设 $H_1$ ：观测数据与理论分布不一致，即合格品的比例不是95%，不合格品的比例不是5%

步骤二：收集数据

观测数据里有90个合格品和10个次品

步骤三：计算期望频数

预期的合格数量为95个

预期的不合格品数量为5个

步骤四：计算卡方统计量

$\chi^2 =\sum \frac{(O_i-E_i)^2}{E_i}$

卡方统计量为 $\chi^2 =\frac{(90-95)^2}{95}+\frac{(10-5)^2}{5}$

步骤五：确定自由度

自由度为类别数减一，总共只有合格不合格两个类别，因此自由度为1

步骤六：确定p值，得出结论

根据选定的p值，比如p=0.05，判断是否拒绝原假设

这个过程可以写成如下的python代码形式

from scipy.stats import chisquare # 观测频数 observed = [90, 10] # 预期频数，基于95%和5%的比例 expected = [100 * 0.95, 100 * 0.05] # 执行卡方拟合优度检验 chi2, p = chisquare(f_obs=observed, f_exp=expected) print("卡方统计量:", chi2) print("P值:", p) # 显著性水平 alpha = 0.05 if p < alpha: print("在显著性水平为 {:.2f} 的情况下，拒绝原假设。".format(alpha)) else: print("在显著性水平为 {:.2f} 的情况下，不能拒绝原假设。".format(alpha))

运行结果如下：

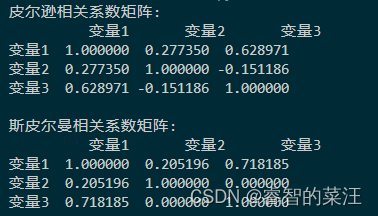
可以看到，在5%的显著性水平上拒绝了原假设。

应用场景3

卡方同质性检验：假设我们有来自三个不同地区的数据，想要检验这三个地区的人口年龄分布是否相同。我们可以收集每个地区不同年龄段的人口数量，构建列联表，并使用卡方同质性检验来确定这三个地区的人口年龄分布是否具有统计学上的同质性。

步骤一：假设提出

原假设 $H_0$ ：三个地区的人口年龄分布是相同的。

备择假设 $H_1$ ：至少有一个地区的人口年龄分布与其他地区不同。

步骤二：收集数据

收集每个地区不同年龄段的人口数量。例如，假设我们有四个年龄段：0-20, 21-40, 41-60, 61+。

步骤三：构建列联表

创建一个列联表，行表示地区，列表示年龄段，单元格中的数值为该年龄段在对应地区的人口数量。

步骤四：计算期望频数

期望频数同样由 $E_{ij}=\frac{Row_i*Col_j}{Sum}$ 给出

其中 $Row_i$ 表示第i行的行总和， $Col_j$ 表示第j列的列总和， $Sum$ 表示总计

步骤五：计算卡方统计量

同样使用以下公式计算卡方统计量：

$\chi^2=\sum{\frac{(O_{ij}-E_{ij})^2}{E_{ij}}}$

其中 $O_{ij}$ 表示第i行第j列的观测值， $E_{ij}$ 为步骤二中计算出来的值

步骤六：确定自由度

卡方分布的自由度为行数减一乘以列数减一，计算公式为：

$df=(Row-1)(Col-1)$

步骤七：确定p值，得出结论

使用卡方分布表或统计软件，根据卡方统计量和自由度确定P值。如果P值小于显著性水平（例如0.05），则拒绝原假设，认为至少有一个地区的人口年龄分布与其他地区不同。如果P值大于或等于显著性水平，则不能拒绝原假设，认为三个地区的人口年龄分布是相同的。

应用场景4

虽然卡方分布通常不直接用于测量相关性，但在某些情况下，比如列联表中两个分类变量的相关性检验，可以使用卡方统计量。例如，我们想要检验不同血型（A、B、AB、O）和某种疾病发生率之间的关系。通过收集不同血型人群的疾病发生率数据，构建列联表，并进行卡方检验，我们可以评估血型和疾病发生率之间是否存在统计学上的关联。

同样的步骤，这里不再赘述。卡方分布虽然可以做，但是这个应用场景的情况下使相关系数的方法可能会更多。相关系数矩阵打印的python方法如下：

import pandas as pd from scipy.stats import pearsonr from scipy.stats import spearmanr # 创建一个示例数据集 data = { '变量1': [20, 21, 19, 20, 22], '变量2': [12, 11, 13, 14, 15], '变量3': [88, 99, 91, 92, 95] } # 将数据转换为pandas DataFrame df = pd.DataFrame(data) # 计算皮尔逊相关系数矩阵 pearson_matrix = df.corr(method='pearson') # 打印皮尔逊相关系数矩阵 print("皮尔逊相关系数矩阵:") print(pearson_matrix) # 如果需要计算斯皮尔曼相关系数矩阵 spearman_matrix = df.corr(method='spearman') # 打印斯皮尔曼相关系数矩阵 print("\n斯皮尔曼相关系数矩阵:") print(spearman_matrix)

运行结果如下：

如上就是卡方分布的一些应用实例。

【本文地址】

公司简介

联系我们