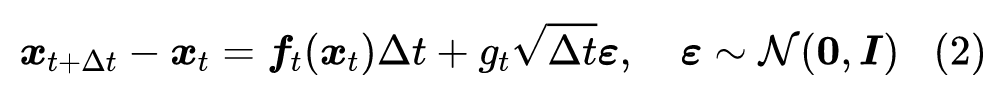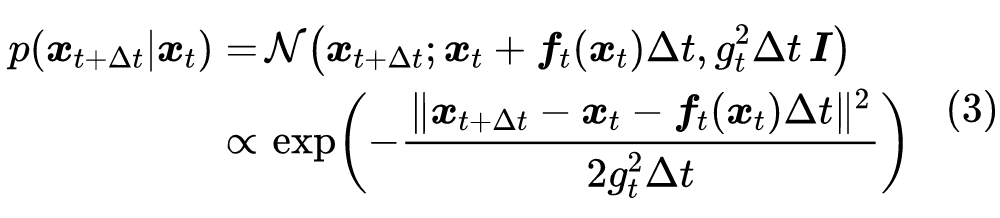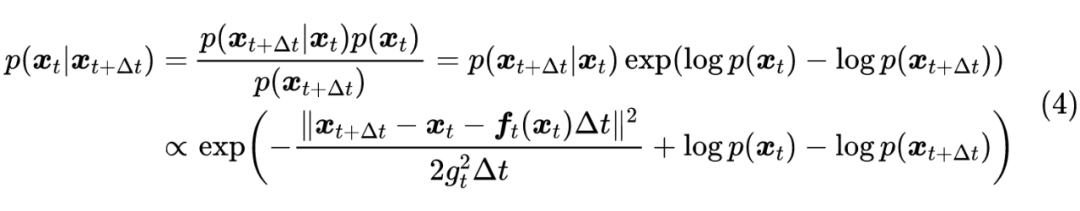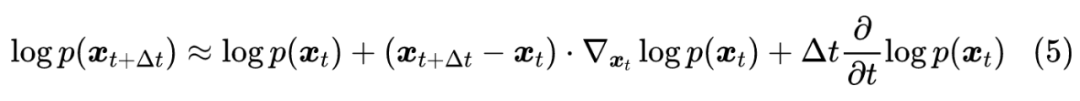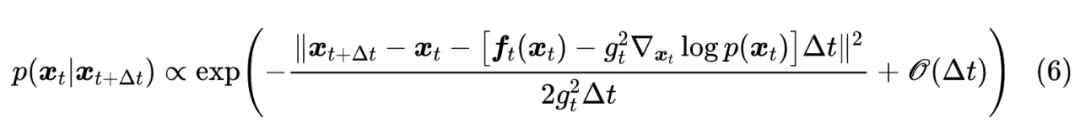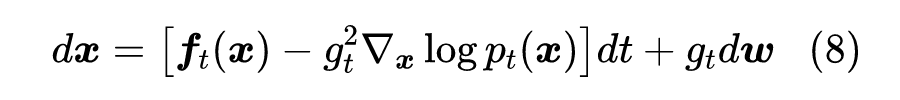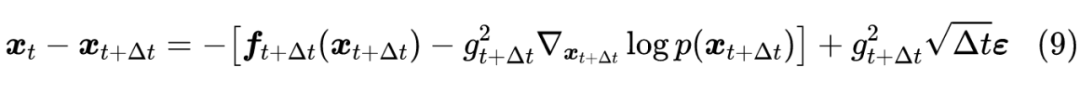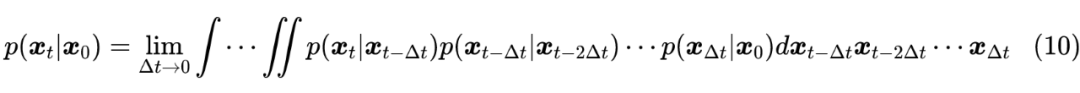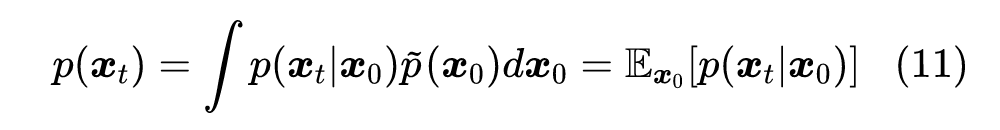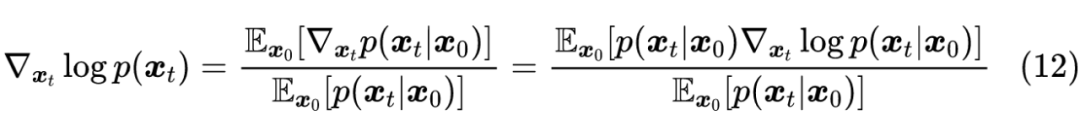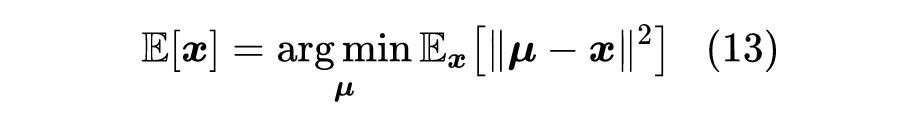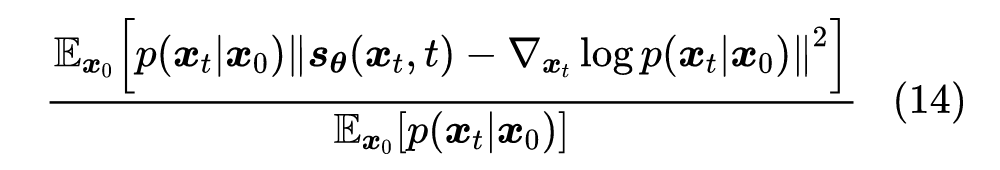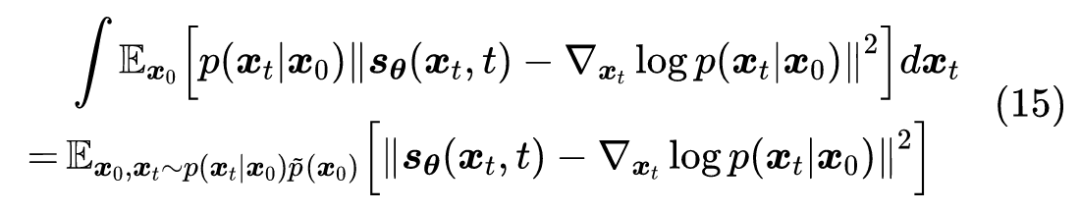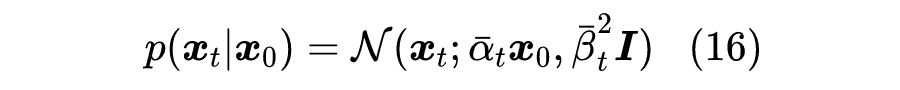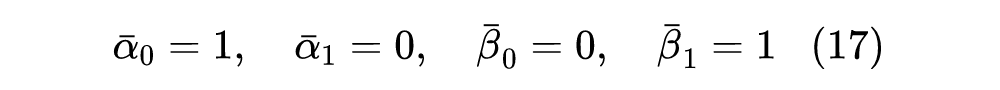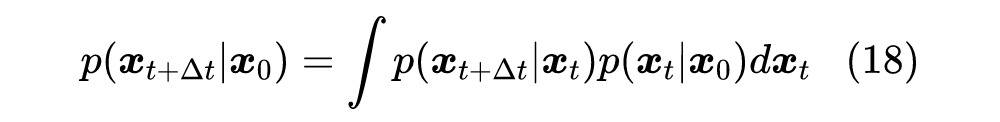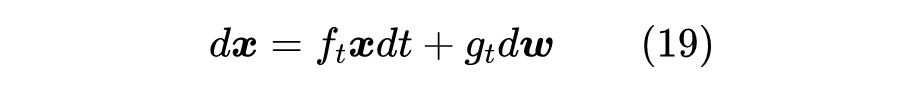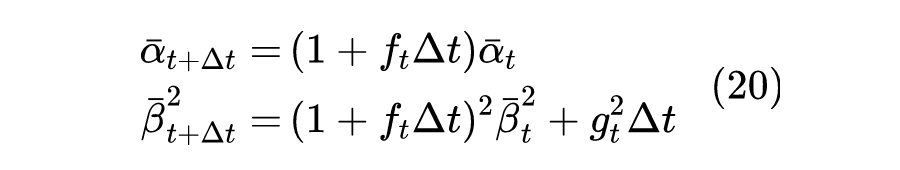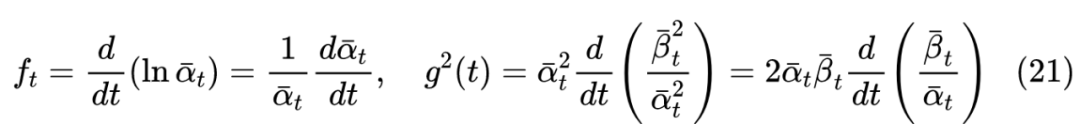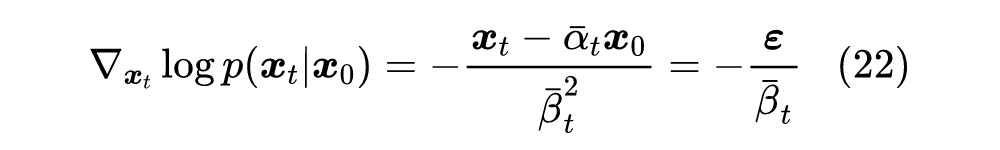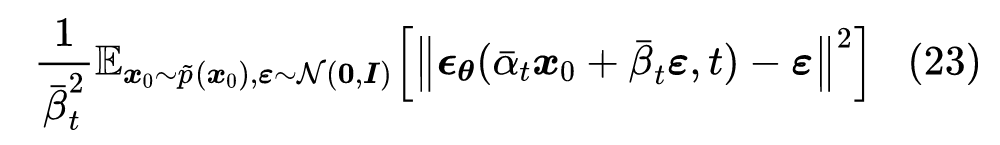生成扩散模型漫谈：一般框架之SDE篇

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在写生成扩散模型的第一篇文章时，就有读者在评论区推荐了宋飏博士的论文《Score-Based Generative Modeling through Stochastic Differential Equations》[1]，可以说该论文构建了一个相当一般化的生成扩散模型理论框架，将 DDPM、SDE、ODE 等诸多结果联系了起来。诚然，这是一篇好论文，但并不是一篇适合初学者的论文，里边直接用到了随机微分方程（SDE）、Fokker-Planck 方程、得分匹配等大量结果，上手难度还是颇大的。

不过，在经过了前四篇文章的积累后，现在我们可以尝试去学习一下这篇论文了。在接下来的文章中，笔者将尝试从尽可能少的理论基础出发，尽量复现原论文中的推导结果。

随机微分

在 DDPM 中，扩散过程被划分为了固定的 步，还是用《生成扩散模型漫谈：DDPM = 拆楼 + 建楼》的类比来说，就是“拆楼”和“建楼”都被事先划分为了 步，这个划分有着相当大的人为性。事实上，真实的“拆”、“建”过程应该是没有刻意划分的步骤的，我们可以将它们理解为一个在时间上连续的变换过程，可以用随机微分方程（Stochastic Differential Equation，SDE）来描述。

为此，我们用下述 SDE 描述前向过程（“拆楼”）：

相信很多读者都对 SDE 很陌生，笔者也只是在硕士阶段刚好接触过一段时间，略懂皮毛。不过不懂不要紧，我们只需要将它看成是下述离散形式在 时的极限：

再直白一点，如果假设拆楼需要 天，那么拆楼就是 从 到 的变化过程，每一小步的变化我们可以用上述方程描述。至于时间间隔 ，我们并没有做特殊限制，只是越小的 意味着是对原始 SDE 越好的近似，如果取 ，那就对应于原来的 ，如果是 则对应于 ，等等。也就是说，在连续时间的 SDE 视角之下，不同的 是 SDE 不同的离散化程度的体现，它们会自动地导致相似的结果，我们不需要事先指定 ，而是根据实际情况下的精确度来取适当的 T 进行数值计算。

所以，引入 SDE 形式来描述扩散模型的本质好处是“将理论分析和代码实现分离开来”，我们可以借助连续性 SDE 的数学工具对它做分析，而实践的时候，则只需要用任意适当的离散化方案对 SDE 进行数值计算。

对于式（2），读者可能比较有疑惑的是为什么右端第一项是 的，而第二项是 的？也就是说为什么随机项的阶要比确定项的阶要高？这个还真不是那么容易解释，也是 SDE 比较让人迷惑的地方之一。简单来说，就是 一直服从标准正态分布，如果随机项的权重也是 ，那么由于标准正态分布的均值为 、协方差为 ，临近的随机效应会相互抵消掉，要放大到 才能在长期结果中体现出随机效应的作用。

逆向方程

用概率的语言，式（2）意味着条件概率为：

简单起见，这里没有写出无关紧要的归一化因子。按照 DDPM 的思想，我们最终是想要从“拆楼”的过程中学会“建楼”，即得到 ，为此，我们像《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》一样，用贝叶斯定理：

不难发现，当 足够小时，只有当 与 足够接近时， 才会明显不等于 0，反过来也只有这种情况下 才会明显不等于 0。因此，我们只需要对 与 足够接近时的情形做近似分析，为此，我们可以用泰勒展开：

注意不要忽略了 项，因为 实际上是“ 时刻随机变量等于 的概率密度”，而 实际上是“ 时刻随机变量等于 的概率密度”，也就是说 实际上同时是 和 的函数，所以要多一项 的偏导数。代入到式（4）后，配方得到：

当 时， 不起作用，因此：

即 近似一个均值为 、协方差为 的正态分布，取 的极限，那么对应于 SDE：

这就是反向过程对应的 SDE，最早出现在《Reverse-Time Diffusion Equation Models》[2] 中。这里我们特意在 处标注了下标 ，以突出这是 时刻的分布。

得分匹配

现在我们已经得到了逆向的 SDE 为（8），如果进一步知道 ，那么就可以通过离散化格式：

来逐步完成“建楼”的生成过程【其中 】，从而完成一个生成扩散模型的构建。

那么如何得到 呢？ 时刻的 就是前面的 ，它的含义就是 时刻的边缘分布。在实际使用时，我们一般会设计能找到 解析解的模型，这意味着：

是可以直接求出的，比如当 是关于 的线性函数时， 就可以解析求解。在此前提下，有：

于是：

可以看到最后的式子具有“ 的加权平均”的形式，由于假设了 有解析解，因此上式实际上是能够直接估算的，然而它涉及到对全体训练样本 的平均，一来计算量大，二来泛化能力也不够好。因此，我们希望用神经网络学一个函数 ，使得它能够直接计算 。

很多读者应该对如下结果并不陌生（或者推导一遍也不困难）：

也就是说，要让 等于 的均值，只需要最小化 的均值。同样地，要让 等于 的加权平均【即 】，则只需要最小化 的加权平均，即：

分母的 只是起到调节 Loss 权重的作用，简单起见我们可以直接去掉它，这不会影响最优解的结果。最后我们再对 积分（相当于对于每一个 都要最小化上述损失），得到最终的损失函数：

这就是“（条件）得分匹配”的损失函数，之前我们在《从去噪自编码器到生成模型》推导的去噪自编码器的解析解，也是它的一个特例。得分匹配的最早出处可以追溯到 2005 年的论文《Estimation of Non-Normalized Statistical Models by Score Matching》[3]，至于条件得分匹配的最早出处，笔者追溯到的是 2011 年的论文《A Connection Between Score Matching and Denoising Autoencoders》[4]。

不过，虽然该结果跟得分匹配是一样的，但其实在这一节的推导中，我们已经抛开了“得分”的概念了，纯粹是由目标自然地引导出来的答案，笔者认为这样的处理过程更有启发性，希望这一推导能降低大家对得分匹配的理解难度。

结果倒推

至此，我们构建了生成扩散模型的一般流程：

1. 通过随机微分方程（1）定义“拆楼”（前向过程）；

2. 求 的表达式；

3. 通过损失函数（15）训练 （得分匹配）；

4. 用 替换式（8）的 ，完成“建楼”（反向过程）。

可能大家看到 SDE、微分方程等字眼，天然就觉得“恐慌”，但本质上来说，SDE 只是个“幌子”，实际上将对 SDE 的理解转换到式（2）和式（3）上后，完全就可以抛开 SDE 的概念了，因此概念上其实是没有太大难度的。

不难发现，定义一个随机微分方程（1）是很容易的，但是从（1）求解 却是不容易的。原论文的剩余篇幅，主要是对两个有实用性的例子推导和实验。然而，既然求解 不容易，那么按照笔者的看法，与其先定义（1）再求解 ，倒不如像 DDIM [5] 一样，先定义 ，然后再来反推对应的 SDE？

例如，我们先定义：

并且不失一般性假设起点是 ，终点是 ，那么 要满足的边界就是：

当然，上述边界条件理论上足够近似就行，也不一定非要精确相等，比如上一篇文章我们分析过 DDPM 相当于选择了 ，当 时结果为 。

有了 ，我们去反推（1），本质上就是要求解 ，它要满足：

我们考虑线性的解，即：

跟《生成扩散模型漫谈：DDIM = 高观点DDPM》一样，我们写出：

由此可得：

令 ，分别解得：

取 时，结果就是论文中的 VE-SDE（Variance Exploding SDE）；而如果取 时，结果就是原论文中的 VP-SDE（Variance Preserving SDE）。

至于损失函数，此时我们可以算得：

第二个等号是因为 ，为了跟以往的结果对齐，我们设 ，此时式（15）为：

忽略系数后就是 DDPM 的损失函数，而用 替换掉式（9）的 后，结果与 DDPM 的采样过程具有相同的一阶近似（意味着 时两者等价）。

文章小结

本文主要介绍了宋飏博士建立的利用 SDE 理解扩散模型的一般框架，其中包括以尽可能直观的语言推导了反向 SDE、得分匹配等结果，并对方程的求解给出了自己的想法。

参考文献

[1] https://arxiv.org/abs/2011.13456

[2] https://www.sciencedirect.com/science/article/pii/0304414982900515

[3] https://www.jmlr.org/papers/v6/hyvarinen05a.html

[4]https://www.iro.umontreal.ca/~vincentp/Publications/DenoisingScoreMatching_NeuralComp2011.pdf

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：[email protected] 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·