【物理数学】莱布尼兹积分法则

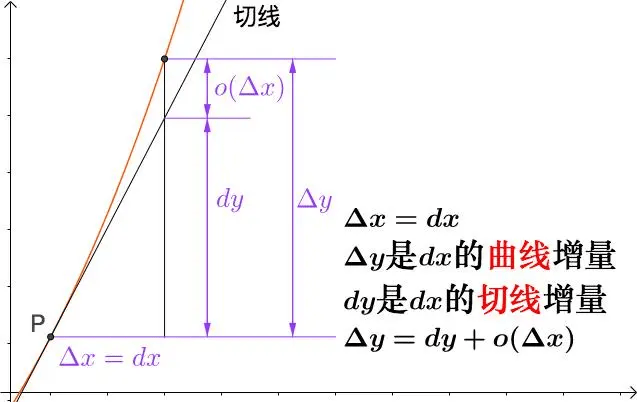
02

莱布尼兹积分法则的数学原理

莱布尼兹积分法则的核心在于处理函数乘积的导数问题。在微分学中，我们知道如何对单个函数进行微分，但当我们面对两个或多个函数的乘积时，情况就变得复杂起来。莱布尼兹积分法则为我们提供了一种方法，可以将乘积的导数分解为更简单的形式。具体来说，如果我们有两个可微函数u(x)和v(x)，那么它们的乘积的导数可以表示为：

d/dx[u(x)v(x)] = u'(x)v(x) + u(x)v'(x)

这个法则实际上是乘积法则在微分学中的体现，它允许我们将一个复杂的微分问题分解为两个更简单的问题。这一原理在物理学中的应用尤为广泛，例如，在计算力和速度的乘积以得到功率时，莱布尼兹法则就发挥了关键作用。

为了更深入地理解这一法则，我们可以考虑一个具体的例子。假设我们有一个简单的摆动，其角度随时间变化的函数为θ(t)。如果我们想要计算角速度ω(t)，即角度随时间的变化率，我们可以使用莱布尼兹法则。角速度可以表示为：

ω(t) = d/dt[θ(t)]

如果我们进一步考虑一个摆的线性位移x(t)与角度θ(t)的关系，即x(t) = lθ(t)，其中l是摆长，那么我们可以通过莱布尼兹法则来计算位移对时间的导数，即速度v(t)：

v(t) = d/dt[x(t)] = d/dt[lθ(t)] = l * d/dt[θ(t)] = lω(t)

这个例子展示了莱布尼兹法则如何帮助我们从已知的角度变化函数得到速度函数。

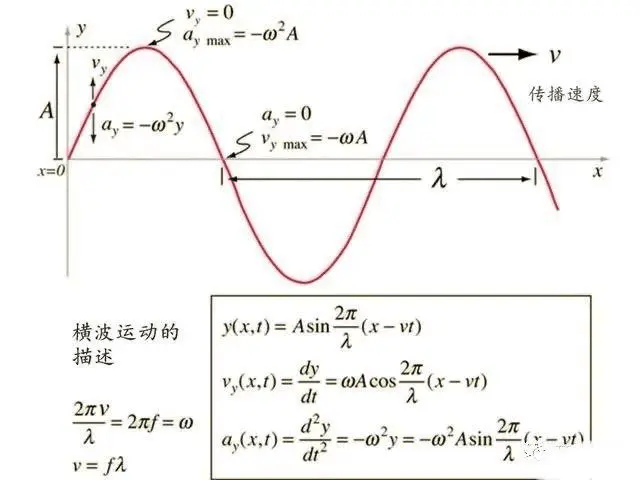
03

莱布尼兹积分法则的应用实例

莱布尼兹积分法则在实际应用中同样发挥着重要作用。例如，在物理学中，当我们需要计算一个物体在受力作用下的加速度时，我们通常会涉及到力和速度的乘积。通过莱布尼兹积分法则，我们可以轻松地找到加速度的表达式，从而预测物体的运动状态。

让我们通过一个具体的例子来展示莱布尼兹积分法则的应用。假设我们有一个简单的弹簧振子模型，其位移x随时间t的变化由以下公式给出：

x(t) = A cos(ωt)

其中A是振幅，ω是角频率。现在，我们想要计算振子的速度v(t)，速度是位移对时间的导数。根据莱布尼兹法则，我们可以得到：

v(t) = d/dt[x(t)] = d/dt[A cos(ωt)] = -Aωsin(ωt)

通过这个例子，我们可以看到莱布尼兹法则如何帮助我们从已知的位移函数得到速度函数。这一原理在物理学中有着广泛的应用，特别是在处理振动和波动问题时。

在人类文明进程中的这些具有里程碑意义的发明和发现背后，微积分究竟扮演了什么样的角色？围绕曲线之谜、运动之谜和变化之谜，毕达哥拉斯、阿基米德、伽利略、开普勒、牛顿、莱布尼茨、爱因斯坦、薛定谔等如何用微积分的“钥匙”打开了宇宙奥秘之“锁”？这些谜题的解决方案对人类文明的进程和我们的日常生活又产生了什么样的深远影响？

在《微积分的力量》书中，应用数学家兼“导游”斯托加茨将用一种“讲故事”和“看展览”的方式为你逐一揭晓答案。“我们不必为了理解微积分的重要性而学习如何做运算，就像我们不必为了享用美食而学习如何做佳肴一样。我将借助图片、隐喻和趣闻逸事等，尝试解释你们需要了解的关于微积分的知识。我也会给你们介绍有史以来颇为精致的一些方程和证明，就像我们在参观画展的时候不会错过其中的代表作一样。” 在高中和大学时期，尽管我们中的许多人都对这门课程退避三舍，但斯托加茨用一种新颖独特和接地气儿的方式给我们讲述了微积分的历史。相信在读完《微积分的力量》后，我们都会对微积分有更加立体生动的认知，就像欣赏名画、名曲那样发现微积分之美。

04

莱布尼兹积分法则的推广

莱布尼兹积分法则的推广涉及到积分而非导数。在积分学中，我们有时会遇到需要计算两个函数乘积的积分的情况。莱布尼兹积分法则的推广形式提供了一种方法，可以将这种积分分解为两个单独积分的和。然而，这个推广形式并不总是成立，它要求函数在积分区间上满足一定的条件。

例如，如果我们有两个连续函数u(x)和v(x)，并且它们在区间[a, b]上可积，那么我们可以写出：

∫[a, b] u(x)v(x) dx = ∫[a, b] u(x) dx * v(b) - ∫[a, b] u(x) dx * v(a)

这个公式在计算某些类型的积分时非常有用，尤其是当积分的计算变得复杂时。然而，需要注意的是，这个公式只在u(x)和v(x)在区间[a, b]上连续且可积的条件下成立。

05

结论

莱布尼兹积分法则是微积分学中的一个基本工具，它不仅在理论上具有重要意义，而且在实际应用中也有着广泛的用途。通过本文的介绍，我们希望能够增强读者对这一数学原理的理解，并激发他们对微积分更深层次探索的兴趣。莱布尼兹的工作不仅推动了数学的发展，也为现代科学的进步奠定了基础。他的法则至今仍然是解决复杂数学问题的有力工具。

参考文献

1. Leibniz, G. W. (1684). Nova Methodus pro Maximis et Minimis, Itemque Tangentibus, Sectio Analytica. Acta Eruditorum, 167–170.

2. Newton, I. (1687). Philosophiæ Naturalis Principia Mathematica. London: Josephi Streater.

3. Spivak, M. (1965). Calculus. New York: Publish or Perish, Inc.

文章来源于数学与人工智能，转载旨在分享，如有侵权请联系删除。‍

免责声明：自媒体综合提供的内容均源自自媒体，版权归原作者所有，转载请联系原作者并获许可。文章观点仅代表作者本人，不代表环球物理立场。

环球物理

ID：huanqiuwuli

环球物理，以物理学习为主题，以传播物理文化为己任。专业于物理，致力于物理！以激发学习者学习物理的兴趣为目标，分享物理的智慧，学会用物理思维去思考问题，为大家展现一个有趣，丰富多彩的，神奇的物理。

投稿请联系 [email protected]返回搜狐，查看更多