| 数字电子技术之逻辑代数基础 | 您所在的位置:网站首页 › 数字电子技术逻辑代数公式化简例题 › 数字电子技术之逻辑代数基础 |
数字电子技术之逻辑代数基础
|
布尔与布尔代数基础公式吸收定律多余项定律摩根定律逻辑运算的优先级带入定律对偶定律逻辑函数的基本形式
逻辑代数是由英国数学家乔治布尔首先提出来的,由此也称为布尔代数。 后来,美国数学家香农将布尔代数应用于开关矩阵电路中,因而逻辑代数又称为开关代数。 在计算机程序语言中,用布尔的名字命名了一种变量形式: Boole型变量,取值为True (真)、False (假)。 2. 基础公式 2.1常量与常量之间的逻辑关系常量与常量之间的与、或、非:
[例]证明公式: A + BC = (A + B)(A + C) 真值表判定法
(A + B)(A + C) = A + AC + AB + BC = A(1 + C + B) + BC = A + BC 很明显,公式推导法相比于真值表判定法来说,要更简单些 3. 吸收定律
AB + A B ‾ \overline{\text{B}} B = A --> 消相邻项 [例]: (1) F = ABC + A B ‾ \overline{\text{B}} BC = AC (2) F = AC + BC + A + B ‾ \overline{\text{A + B}} A + BC = (A + B)C + A + B ‾ \overline{\text{A + B}} A + BC = C (3) F = ABC D ‾ \overline{\text{D}} D + AB C ‾ \overline{\text{C}} C D ‾ \overline{\text{D}} D = AB D ‾ \overline{\text{D}} D 吸收定律2A +AB = A -->消多余项 [例]: (1) F = A + AB + A C ‾ \overline{\text{C}} C + A ‾ \overline{\text{A}} ABC D ‾ \overline{\text{D}} D = A + A ‾ \overline{\text{A}} ABC D ‾ \overline{\text{D}} D 吸收定律3A + A ‾ \overline{\text{A}} AB = A + B -->消多余因子 [例]: (1) F = A + A ‾ \overline{\text{A}} ABC D ‾ \overline{\text{D}} D = A + BC D ‾ \overline{\text{D}} D (2) F = A + B + A ‾ \overline{\text{A}} A B ‾ \overline{\text{B}} BCD = A + B + B ‾ \overline{\text{B}} BCD = A + B + CD 这里也可以推导出 A ‾ \overline{\text{A}} A ⋅ \cdot ⋅ B ‾ \overline{\text{B}} B = A + B ‾ \overline{\text{A + B}} A + B 4. 多余项定律
已知 F = A + B + C + D ,求反函数 F ‾ \overline{\text{F}} F 解: F ‾ \overline{\text{F}} F = A + B + C + D ‾ \overline{\text{A + B + C + D}} A + B + C + D = A + B ‾ \overline{\text{A + B}} A + B ⋅ \cdot ⋅ C + D ‾ \overline{\text{C + D}} C + D = A ‾ \overline{\text{A}} A ⋅ \cdot ⋅ B ‾ \overline{\text{B}} B ⋅ \cdot ⋅ C ‾ \overline{\text{C}} C ⋅ \cdot ⋅ D ‾ \overline{\text{D}} D 摩根定律的推广二
在利用摩根定律做这道题时,会得到两个答案:
因此回过头来看刚刚的例题,右边的答案才是正确的: 在任何包含变量A的逻辑公式中,若以另外一个逻辑表达式带入公式中所有A的位置(即替换A ) ,公式仍然成立。 8. 对偶定律与摩根定律第二个推广的不同: “与”、"或"对调;0、1对调变量不变长非号不变,保证原先运算优先级异或、同或对调
通过对偶定律可以得到以下推广:
[例]已知逻辑表达式F= AB+ A ‾ \overline{\text{A}} AC,将其转换为其他几类常见形式:
先求出反函数的与或式,再取反一次 ,不处理即可: 与或非式用摩根定律展开两层,得到或与式: 或与式两次取反,用摩根定律展开一层: |
【本文地址】


 这两组公式为对偶关系,名字并不重要
这两组公式为对偶关系,名字并不重要

 吸收定律1、2、3:
吸收定律1、2、3: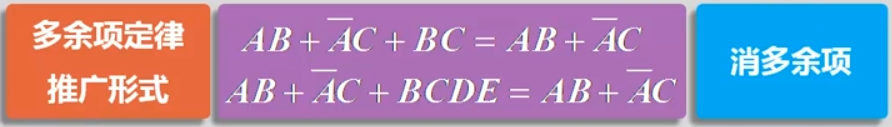
 [例]: (1) F = AB +
B
‾
\overline{\text{B}}
BC + AC + A
B
‾
\overline{\text{B}}
BC
D
‾
\overline{\text{D}}
DE = AB +
B
‾
\overline{\text{B}}
BC --> 消去多余项AC (2) F =
A
‾
\overline{\text{A}}
ABC + A
B
‾
\overline{\text{B}}
BC +
A
‾
\overline{\text{A}}
A
B
‾
\overline{\text{B}}
BD + ABD + CDE
[例]: (1) F = AB +
B
‾
\overline{\text{B}}
BC + AC + A
B
‾
\overline{\text{B}}
BC
D
‾
\overline{\text{D}}
DE = AB +
B
‾
\overline{\text{B}}
BC --> 消去多余项AC (2) F =
A
‾
\overline{\text{A}}
ABC + A
B
‾
\overline{\text{B}}
BC +
A
‾
\overline{\text{A}}
A
B
‾
\overline{\text{B}}
BD + ABD + CDE 
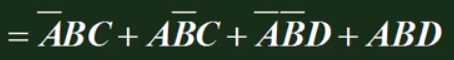 (3) F = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
C
‾
\overline{\text{C}}
C +
B
‾
\overline{\text{B}}
BC 这题没有可以直接消去的项,我们根据后两项可以加一项,等式仍然成立: F = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
C
‾
\overline{\text{C}}
C +
B
‾
\overline{\text{B}}
BC + A
B
‾
\overline{\text{B}}
B = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
B
‾
\overline{\text{B}}
B
(3) F = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
C
‾
\overline{\text{C}}
C +
B
‾
\overline{\text{B}}
BC 这题没有可以直接消去的项,我们根据后两项可以加一项,等式仍然成立: F = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
C
‾
\overline{\text{C}}
C +
B
‾
\overline{\text{B}}
BC + A
B
‾
\overline{\text{B}}
B = B
C
‾
\overline{\text{C}}
C +
A
‾
\overline{\text{A}}
AC + A
B
‾
\overline{\text{B}}
B 摩根定律的由来:
摩根定律的由来:  证明过程:
证明过程: 
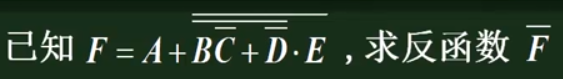
 对比原函数和反函数:
对比原函数和反函数: 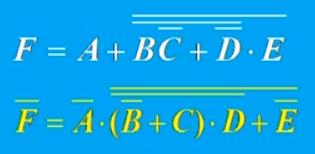 可以发现如下规律:
可以发现如下规律: 这时就要提到运算的优先级了
这时就要提到运算的优先级了 异或和同或是同级运算,且优先级低于乘,高于加
异或和同或是同级运算,且优先级低于乘,高于加
 使用对偶定律,可以根据一个成立的逻辑公式,得到与其结构上满足对偶关系的新公式。
使用对偶定律,可以根据一个成立的逻辑公式,得到与其结构上满足对偶关系的新公式。 对偶定律的推广:
对偶定律的推广:  对偶公式表:
对偶公式表: 
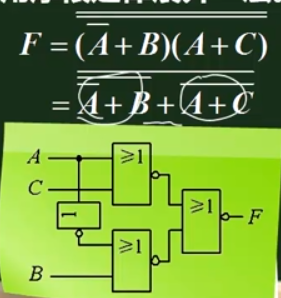
 逻辑函数的形式多种多样,每-种表达式,都对应着一种电路组成形式,表示一个确定的逻辑电路。
逻辑函数的形式多种多样,每-种表达式,都对应着一种电路组成形式,表示一个确定的逻辑电路。

 最后再加个非号:
最后再加个非号: