| 梯度、散度、旋度 | 您所在的位置:网站首页 › 散度梯度旋度释义pdf › 梯度、散度、旋度 |
梯度、散度、旋度
|
前言 感谢视频作者,无意间刷到,把旋度和散度讲的很通俗易懂,可视化也很直观。本文为学习笔记。 https://player.bilibili.com/player.html?aid=468216938&bvid=BV1a541127cX&cid=574493213&page=1&high_quality=1 结论:理解1: 散度是通量的体密度,即通量的微分; 旋度是环量的面密度,即环量的微分;理解2: 区别在于如何与\(\nabla\)进行运算: 数学概念 特点 符号 Numpy函数 梯度 数量积、哈达玛积 \(\odot\) np.multiply 或者 * 散度 点乘、内积 \(\cdot\) np.dot 旋度 叉乘、外积 \(\times\)或者 \(\otimes\) np.cross --- 1. 梯度(graident)对于标量场和矢量场 1.1 对于标量场nabla算子把数量场变成了向量场,即 \(\mathbb{R} \rightarrow \mathbb{R}^n\): \[ \nabla = \begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix}^T \]\(\nabla\)和函数的数量乘\(\nabla f\) 称为函数梯度 \[\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix} \frac{\partial }{\partial x_1}\\ \frac{\partial }{\partial x_2}\\ \vdots \\ \frac{\partial }{\partial x_n} \end{bmatrix} \odot f= \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_1}, \frac{\partial f(\boldsymbol{x})}{\partial x_2},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_n} \right]^T=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}} \]1.2 对矢量场\(m\)维向量函数\(\boldsymbol{f}(\boldsymbol{x})=[f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_m(\boldsymbol{x})]\)相对于\(n\)维实向量\(x\)的梯度为\(n×m\)矩阵,\(\mathbb{R}^{m} \rightarrow \mathbb{R}^{n \times m}\) : \[\nabla\overset{\underset{\mathrm{def}}{}}{=}\begin{bmatrix}\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}\frac{\partial}{\partial x_3}, \dots, \frac{\partial}{\partial x_n}\end{bmatrix}^T \]\[\begin{aligned}\nabla_{\boldsymbol{x}} \boldsymbol{f}(\boldsymbol{x}) &=\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}} \\ & = \begin{bmatrix}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2}\\\frac{\partial}{\partial x_3}\\\vdots\\\frac{\partial}{\partial x_n}\end{bmatrix} \odot\boldsymbol [f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_m(\boldsymbol{x})] \\ &= \begin{bmatrix} \frac{\partial f_1(\boldsymbol{x})}{\partial x_1} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_1} & \cdots & \frac{\partial f_m(\boldsymbol{x})}{\partial x_1} \\ \frac{\partial f_1(\boldsymbol{x})}{\partial x_2} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_2} & \cdots & \frac{\partial f_m(\boldsymbol{x})}{\partial x_2} \\ \vdots &\vdots & \ddots & \vdots \\ \frac{\partial f_1(\boldsymbol{x})}{\partial x_n} &\frac{\partial f_2(\boldsymbol{x})}{\partial x_n} & \cdots &\frac{\partial f_m(\boldsymbol{x})}{\partial x_n} \\ \end{bmatrix} \\ \end{aligned} \]1.3 梯度的性质: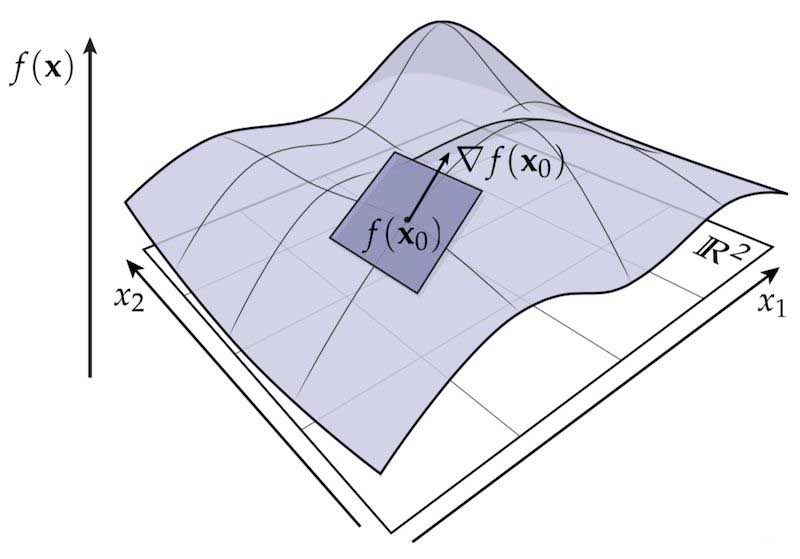 沿着梯度方向走,函数值增大
沿着相反于梯度的方向走,函数值减小
垂直于梯度方向,函数值不变
沿着梯度方向走,函数值增大
沿着相反于梯度的方向走,函数值减小
垂直于梯度方向,函数值不变
--image 2. 散度(divergence)对于向量场 2.1 定义\(\nabla\)和函数的点乘\(\nabla f\) 称为函数散度,某点散度代表了该点向外的通量体密度. \(\mathbb{R}^n \rightarrow \mathbb{R}\)。 设某个三维矢量场为\(f,\) 那么散度 \[\begin{aligned}\mathbf{div} (\mathbb{f}) &= \nabla \cdot f \\&=\begin{bmatrix} {\frac{\partial f_x}{\partial x} , \frac{\partial f_y}{\partial y}, \frac{\partial f_z}{\partial z} }\end{bmatrix}\begin{bmatrix} f_x \\ f_y \\f_x\end{bmatrix}\\&=\frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}\end{aligned} \]这里的\([f_x, f_Y,f_z] = {f} \cdot \vec{n}\) 2.2 高斯公式 👉 **定理: ** 设空间有限比克区域为$\Omega$,$\partial \Omega$ 为该区域的封闭外曲面,那么**高斯公式**: \[ \underbrace{\iiint\limits_\Omega \overbrace{\nabla \cdot {f}}^{散度} dV}_{内部所有散度的贡献} = \underbrace{\oiint\limits_{\partial \Omega}{f} \cdot \vec{n} dS }_{流过边界的通量} \] 对于三维矢量,高斯公式可以表示为: \[\iiint \limits_\Omega (\frac{\partial f_x}{\partial x} + \frac{\partial f_y}{\partial y} + \frac{\partial f_z}{\partial z}) dV = \oiint \limits_{\partial \Omega}f_zdydz+f_ydxdz+f_zdxdy \]--image 物理意义: 某点散度代表了该点向外的通量体密度,其物理意义可以理解为:定量给出向量场中任一点是否为源点或汇点。若某点散度等于0,则说明其通量为0,流进=流出;若某点散度大于0,说明流出>流进,相当于一个源点(source);若某点散度小于0,说明流出 |
【本文地址】