麦克斯韦方程组

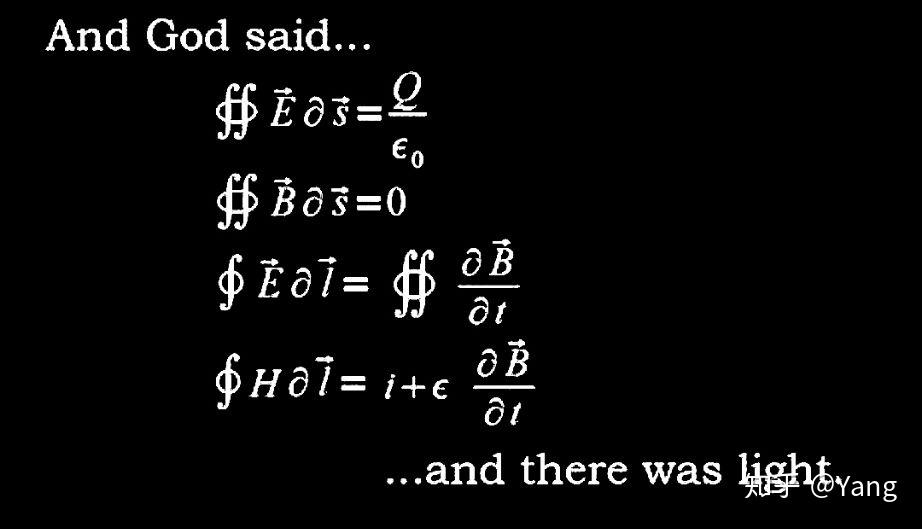本文只介绍真空中麦克斯韦方程组的推导，介质中的方程先不管了。而且下面将推导出微分形式，因为微分形式比积分形式简洁，并且能够处理局域的电磁现象，而积分形式往往不太方便。

首先把微分形式的方程先写在下面，然后再一个一个地说明：

\nabla \cdot \vec E=\frac{\rho}{\varepsilon_0}（高斯定理）

\nabla \cdot \vec B=0（安培环路定律）

\nabla \times \vec E=-\frac{\partial \vec B}{\partial t}（电磁感应）

\nabla \times \vec B = \mu_0 \vec J+\mu_0\varepsilon_0 \frac{\partial \vec E}{\partial t}（麦克斯韦位移电流）

①高斯定理

下面先看第一个，也就是\nabla \cdot \vec E=\frac{\rho}{\varepsilon_0}，一般叫做高斯定理。这个方程比较简单，很容易就看得出来它所表达的意思。方程\nabla \cdot \vec E=\frac{\rho}{\varepsilon_0}的意思就是说， \frac{\rho}{\varepsilon_0} 就是就是电场 \vec E 在这个点的散度大小。

下面就正式开始推导：

先证明高斯定理的积分形式，这必须从最基本的原理出发，那就是库仑定律，根据库仑定律容易得到一个静止点电荷激发电场的表达式： \vec E=\frac{Q\vec r}{4\pi \varepsilon_0 r^3}

现在想象一个闭合曲面 S ， d\vec S 为曲面上的定向面元，每个面元都垂直于曲面指向外面。

这时候通过 d\vec S 的面元的通量就是 \vec E\cdot d\vec S=E\cos \theta dS=\frac{Q}{4\pi\varepsilon_0 r^2}\cos \theta dS 。

因为 \cos \theta \frac{dS}{r^2} 就是面元对点电荷 Q d张开的立体角元 d\Omega 。

(这里用到了立体角的定义，如果没见过，可以去网上查一下)

所以整个曲面 S 的通量就是 \oint _S \vec E\cdot d\vec S=\frac{Q}{4\pi \varepsilon_0}\oint d\Omega=\frac{Q}{\varepsilon_0} ，这里用到了闭合曲面的立体角积分为 4\pi 。

现在就得到了高斯定理的积分形式 \oint _S \vec E\cdot d\vec S=\frac{Q}{\varepsilon_0}，容易得到，当电荷分布在空间中的电荷密度为 \rho 的时候，高斯定律可以变成 \oint _S \vec E\cdot d\vec S=\frac{1}{\varepsilon_0}\oint _V\rho dV 。

现在将体积 V 缩小并趋于零，并且由散度的定义 \nabla\cdot\vec f=\lim_{\Delta V\to 0}\frac{\oint \vec f\cdot d\vec S}{\Delta V} ,就可以得到\nabla \cdot \vec E=\frac{\rho}{\varepsilon_0}。

到此，推导结束。

②安培环路定律

现在看一下第二个公式\nabla \cdot \vec B=0，这个公式是安培定律的微分形式，它说明磁场没有散度的。

下面将从描述磁场的基本定理推导出上面这个公式，要用到的就是毕奥-萨伐尔定律，这个定律像库仑定律一样是实验得到的，所以才能作为后续推导的基础。

由毕奥-萨伐尔定律可以写出磁场和空间中电流密度的关系，即 \vec B(\vec x)=\frac{\mu_0}{4\pi}\int_V\frac{\vec J(\vec x')\times \vec r}{r^3}dV' ，其中 \vec r 是 \vec x' 到 \vec x 的矢径。

下面开始推导，这个推导过程中用到了两个矢量分析的公式：

先用一个公式将上式化为另外的形式\vec B(\vec x)=\frac{\mu_0}{4\pi}\int_V\frac{\vec J(\vec x')\times \vec r}{r^3}dV'=-\frac{\mu_0}{4\pi}\int_V \vec J(\vec x')\times \nabla \frac{1}{r}dV'

下面再用公式 \nabla \cdot (\varphi \vec f)=(\nabla \varphi)\times \vec f+\varphi \nabla\times \vec f 推出：

\nabla \times[\vec J(\vec x')\frac{1}{r}]=(\nabla\frac{1}{r})\times\vec J(\vec x')

因此有\vec B=\frac{\mu_0}{4\pi}\nabla\times\int_V\frac{\vec J(\vec x')}{r}dV'=\nabla\times \vec A，其中 \vec A=\frac{\mu_0}{4\pi}\int_V\frac{\vec J(\vec x')}{r}dV' .

现在又由公式 \nabla\cdot \nabla\times\vec f=0 可得： \nabla \cdot \vec B=\nabla\cdot(\nabla\times \vec A)=0 .

得到公式\nabla \cdot \vec B=0。

这个公式告诉我们磁场没有散度，也就是说磁场中不存在像电荷一样产生电场散度的"磁荷"。

③电磁感应

下面看一下公式\nabla \times \vec E=-\frac{\partial \vec B}{\partial t}所描述的电磁感应现象。它表示磁场的变化会使得电场产生旋度，也就是变化的磁场激发出涡旋的电场。

这个公式比较容易推导，因为它基于法拉第电磁感应定律的积分形式，所以直接就可以得到它的微分形式。

下面开始推导：

首先根据实验可得，感应电动势为 \mathscr{E}=-\frac{d}{dt}\int_S\vec B\cdot d\vec S ，这里的负号是由于感应电动势于规定的环绕方向相反。

因为感应电动势就是绕闭合回路 L 的积分，所以有 \oint_L\vec E\cdot d\vec l=-\frac{d}{dt}\int_S\vec B\cdot d\vec S，

如果 L 是固定回路，则有\oint_L\vec E\cdot d\vec l=-\int_S\frac{\partial\vec B}{\partial t}\cdot d\vec S，

根据旋度的定义直接得到微分形式为\nabla \times \vec E=-\frac{\partial \vec B}{\partial t}。

④麦克斯韦位移电流

下面将推导 \nabla \times \vec B = \mu_0 \vec J+\mu_0\varepsilon_0 \frac{\partial \vec E}{\partial t} ，这个公式告诉我们电场如何产生磁场。

这个公式的推导过于繁杂，所以这里只大概说明一下推导思路。

首先根据矢量分析的一大堆公式以及毕奥-萨伐尔定律推出 \nabla\times\vec B=\mu_0 \vec J ，但这个公式只在恒定电流的情况下成立，于是麦克斯韦假象了一个位移电流 \vec J_D 加在公式中，以表示电场的变化，也就是假设 \nabla\times\vec B=\mu_0 (\vec J+\vec J_D) 。

又根据电荷守恒定律 \nabla\cdot \vec J+\frac{\partial \rho}{\partial t}=0 和电场散度\nabla \cdot \vec E=\frac{\rho}{\varepsilon_0}，可以得到 \nabla\cdot(\vec J+\varepsilon_0\frac{\partial \vec E}{\partial t})=0，因此，我们得到了 位移电流的一个可能的表达式 \vec J_D=\varepsilon_0\frac{\partial \vec E}{\partial t} ，事实证明这样做y是可以的。

因此我们得到了最后这个方程\nabla \times \vec B = \mu_0 \vec J+\mu_0\varepsilon_0 \frac{\partial \vec E}{\partial t}。

它表达的意思就是电流和变化的电场都可以产生涡旋的磁场。

下面简单介绍一下麦克斯韦本人以及他的一些成就与贡献：

[1]郭硕鸿. 电动力学. 3版. 北京：高等教育出版社。